レムニスケート(lemniscate)と2変数関数の最大「PASSLABO様の【面白い解法】実力模試」をMathematicaとWolframAlphaとsympyでやってみたい。

・sympyで、計算結果だけなら4行でできました。ページ後半です。
・WolframAlphaとsympyの平面グラフがでます。
・(未)空間における曲線はできていません。Mathematicaは、途中です。

オリジナル(youtube)

【面白い解法】正答率0%！超進学校の実力模試が難問すぎたwww

【正答率0%なのに!?】面白い別解が届きました

「単位」と「不等式」と「2変数関数の最大」の私の気付き3点です。

長文です。
(？？？この行は、いつものゆうどうです。無視して下さい。今回,会話記録を作成できませんでした。？？？)

「PASSLABO様の4つの条件(目的関数,制約条件?)」およびコメント欄より
①x+yの最大値:目的関数
②実数x,y:制約条件
③x>0,y>0:制約条件
④(x^2 + y^2)^2 = x^2 - y^2:制約条件

私の気付き(1)m?単位です。　④より
(x^2 + y^2)^2 = x^2 - y^2
x,yの単位をmとすると,
左辺の単位は,m^4
右辺の単位は,m^2
(x^2 + y^2)^2 = AB(x^2 - y^2)
この式には、AB=1？ a^2(m^2)? が、隠されている事です。
x+yの単位もm?でした。
???他の過去問で、この技？を使っている問題を、教えてもらうと幸いです。???　

私の気付き(2)不等式に、等号がない。 ③より
x=0,y=0でも,レムニスケートが成り立つ。
x,yの定義域に等号がない。という事は、出題者の意図。
いつものあれで？平面極座標で解きなさい。一択、ヒントでしょうか?
???教えて下さい。0以上、つまり等号があったら都合が悪いのでしょうか???

私の気付き(3)「2変数関数の最大とレムニスケート」を絡めた問題でした。 ④より
参考あり

Mathematicaで

In:
Maximize[{x + y, (x^2 + y^2)^2 == x^2 - y^2}, {x, y}]

Out:
{9/2 Root[-3 - 48 #^2 + 64 #^4& , 2, 0] - 
  4 Root[-3 - 48 #^2 + 64 #^4& , 2, 0]^3, {x -> 
   Root[-3 - 48 #^2 + 64 #^4& , 2, 0], 
  y -> 7/2 Root[-3 - 48 #^2 + 64 #^4& , 2, 0] - 
    4 Root[-3 - 48 #^2 + 64 #^4& , 2, 0]^3}}

??? x+yの値は、実数でした。???

In:
x =        Cos[t]/(1 + Sin[t]^2);
y = Sin[t]*Cos[t]/(1 + Sin[t]^2);
Maximize[{x + y, x > 0, y > 0}, {t}]
N[Maximize[{x + y, x > 0, y > 0}, {t}]]

Out:
(Cos[2 ArcTan[
Root[1 - 8 # + 6 #^2 - 8 #^3 + #^4& , 1, 0]]] + Cos[2 ArcTan[
Root[1 - 8 # + 6 #^2 - 8 #^3 + #^4& , 1, 0]]] Sin[2 ArcTan[
Root[1 - 8 # + 6 #^2 - 8 #^3 + #^4& , 1, 0]]])/(1 + Sin[2 ArcTan[
Root[1 - 8 # + 6 #^2 - 8 #^3 + #^4& , 1, 0]]]^2), {t -> 2 ArcTan[
Root[1 - 8 # + 6 #^2 - 8 #^3 + #^4& , 1, 0]]}}

{1.13975, {t -> 0.271264}}

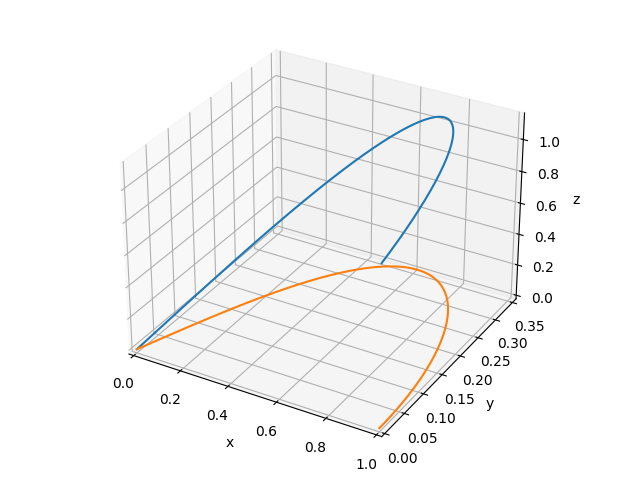
空間における曲線2本を表示しました。
xy平面上に1本と、空間上に1本z=x+yの表示です。
(作図表示省略。アップロードの方法がわからないので。)

p1 = ParametricPlot3D[
   {Cos[t]/(1 + Sin[t]^2), 
    Sin[t]*Cos[t]/(1 + Sin[t]^2), 
    Cos[t]/(1 + Sin[t]^2) + Sin[t]*Cos[t]/(1 + Sin[t]^2)  },
   
   {t, 0, \[Pi]/2}];
p2 = ParametricPlot3D[
   {Cos[t]/(1 + Sin[t]^2), 
    Sin[t]*Cos[t]/(1 + Sin[t]^2), 
    0  },
   
   {t, 0, \[Pi]/2}];
Show[p1, p2]

WolframAlphaで

平面上にレムニスケートの曲線1本の作図だけです。
https://www.wolframalpha.com/input?i=%28x**2%2By**2%29**2+%3D+%281*1%29*%28x**2-y**2%29&lang=ja

(2025-03-06 追加)

sympyで(PASSLABO様の【面白い解法】平面極座標の方法で)

１変数θに直す方法を勉強中です。
積和の公式
特に今回さらにラッキーな事に、一項式?になるみたいです。
以下適当に、x+yの直線の傾き135°だから、
45°-30°= 15°
でもいいですか?

sympyで計算結果だけ(条件式の展開？なら、4行でできました。)

数学の試行錯誤は味わえなくて、申し訳ありません。

from sympy import *
x,y=symbols('x,y',real=True,positive=True)
print("# ",sqrtdenest(sqrtdenest( maximum( (x+solve(  Eq((x**2+y**2)**2,x**2-y**2)  ,y)[0]),x,Interval(0,pi/2) ) ) ) )
#  3**(3/4)/2

sympyで計算だけ(ちょっとくわしく。)

from sympy import *
x,y    =symbols('x,y',real=True,positive=True)
z      =symbols('z'  ,real=True,positive=True)
myCurve=Eq((x**2+y**2)**2,x**2-y**2)
z      =x+y
#
y_Curve=sqrtdenest(sqrtdenest( solve(myCurve,y)[0] ))
z_Curve=z.subs({y:y_Curve})
z_max  =sqrtdenest(sqrtdenest( maximum( z_Curve,x,Interval(0,pi/2) ) ) )
x_ans  =solveset  (Eq(z_Curve,z_max),x,Interval(0,1) ).args[0] 
y_ans  =sqrtdenest(sqrtdenest(y_Curve.subs({x:x_ans})))
t_ans  =Line(Point(0,0),Point(10,0)).angle_between(Line(Point(0,0),Point(x_ans,y_ans)) ).simplify()  
print("# ",z_max,' '*12,float(z_max) )
print("# ",x_ans       ,float(x_ans) )
print("#" ,y_ans       ,float(y_ans) )
print("#" ,t_ans,' '*18,float(t_ans*180/pi)) 
#  3**(3/4)/2              1.1397535284773888
#  3**(1/4)/4 + 3**(3/4)/4 0.8988952674768176
# -3**(1/4)/4 + 3**(3/4)/4 0.24085826100057128
# pi/12                    15.0

sympyで計算だけ(レムニスケートとわかっていれば)

from sympy import *
x,y=symbols('x,y',real=True,positive=True)
t  =symbols('t'  ,real=True,positive=True)
a  =symbols('a'  ,real=True,positive=True)
a=solve(Eq(2*a**2,1),a)[0]
x=2*a**2*(       cos(t))/(1+sin(t)**2)
y=2*a**2*(sin(t)*cos(t))/(1+sin(t)**2)
z=x+y
#
z_max=sqrtdenest(sqrtdenest( maximum( z,t,Interval(0,pi) ) ) ).simplify()
print("# ",z_max,float(z_max))
#  3**(3/4)/2 1.1397535284773888

①私の環境は,pycharmです。
②よく聞くのは、Jupyterです。
③web上で、上記のソースを「SymPy Live shell」に、コピー貼り付けでもできました。
黒背景の右上に、マウスを移動すると、コピーマークが発生します。
???　タブレット環境で、コピー貼り付けが実行できませんでした。???
計算時間は、1分以上かかると思います。

??? sympyで作図

あっているように見えません。
教えて下さい。レムニスケートのカーテン？のイメージです。
plotコマンドは、縦横比？異なります。
implictplot勉強中です。

from sympy import *
from sympy import symbols, cos, sin
from sympy.plotting import plot3d_parametric_line
x,y=symbols('x,y',real=True,positive=True)
t  =symbols('t'  ,real=True,positive=True)
a  =symbols('a'  ,real=True,positive=True)
a  =solve(Eq(2*a**2,1),a)[0]
x  =2*a**2*(       cos(t))/(1+sin(t)**2)
y  =2*a**2*(sin(t)*cos(t))/(1+sin(t)**2)
plot3d_parametric_line( (x,y,x+y, (t,0,pi/2)),
                        (x,y,0  , (t,0,pi/2))
                      )

いつもの? sympyの実行環境と 参考のおすすめです。

(テンプレート)

いつもと違うおすすめです。

参考

def sqrtdenest(expr, max_iter=3):