昨年のhingeありの反力比「(2024)令和6年一級建築士試験学科ⅳ（構造）〔Ｎｏ．２〕」をsympyのBeamでやってみたい。

専門家の方へ　アドバイスをいただけると助かります。
・以下,私は理解できていません。join と hinge です。

公式ホームページ pdf

Qiita_建築士
・目次

オリジナル

・過去問.com 一級建築士 様

いつもの? sympyのweb上での実行方法

・sympyのBeamは、エラーがでます。開発環境は、ページ後半です。
https://qiita.com/mrrclb48z/items/00dd08b0317069be9342#web%E4%B8%8A%E3%81%AE%E5%AE%9F%E8%A1%8C%E6%96%B9%E6%B3%95sympy-live-shell%E3%81%A7

sympyで(オリジナル 様の方法で)

ver0.1

# ver0.1
from sympy import *
var('P,Pab,Pbc,L,EI')
print("#",solve(Eq(Pab*L**3/(3*EI),Pbc*(2*L)**3/(3*2*EI)),Pab)[0]/Pbc) 
# 4

ver0.2

・カスティリアーノの定理で

# ver0.2
from sympy import *
var('P,PA,PB,L,EI,x')
U = 1/(2*   EI )*integrate((PA*x)**2,(x,0,  L)) \
   +1/(2*(2*EI))*integrate((PB*x)**2,(x,0,2*L)) 
sol=solve([Eq(diff(U,PA),diff(U,PB)), \
           Eq(PA+PB,P)],              \
          [PA,PB]
         )
print("#",sol[PA]/sol[PB])
# 4

ver0.3

・sympy の Beamで

# ver0.3
from sympy.physics.continuum_mechanics.beam import Beam
from sympy import *
var('P,E,I,x')             
var('PA,RA,MA')         
var('PC,RC,MC')         
var('l',positive=True)    # positive が,あればいいです。
def my_bA_Cantilever_Def():
    b=Beam(l,E,I)
    b.apply_load(RA,0,-1)
    b.apply_load(MA,0,-2)
    b.apply_load(PA,l,-1)
    b.bc_deflection=[(0,0)]
    b.bc_slope     =[(0,0)]
    return b
def my_bC_Cantilever_Def():
    b=Beam(2*l,2*E,I)
    b.apply_load(PC,0  ,-1)
    b.apply_load(RC,2*l,-1)
    b.apply_load(MC,2*l,-2)
    b.bc_deflection=[(2*l,0)]
    b.bc_slope     =[(2*l,0)]
    return b
bA=my_bA_Cantilever_Def()
bC=my_bC_Cantilever_Def()
bA.solve_for_reaction_loads(RA,MA)
bC.solve_for_reaction_loads(RC,MC)
sol=solve([Eq(bA.deflection().subs({x:l}),   \
              bC.deflection().subs({x:0})),  \
           Eq(P-PA-PC,0)], \
          [PA,PC])
print("#",sol[PA]/sol[PC])
# 4
# -----------------------------------------------
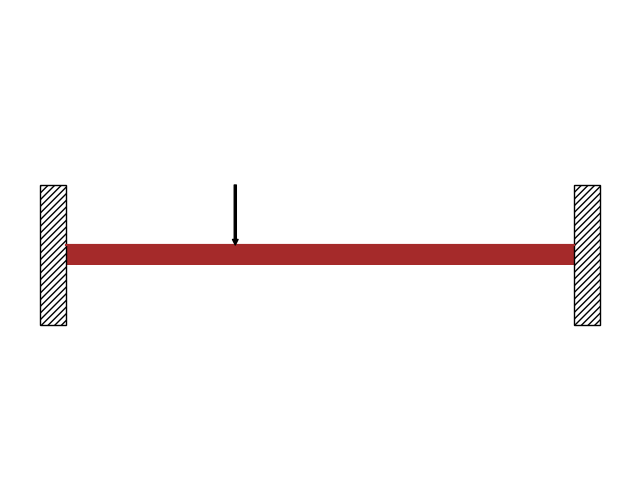
def my_Hinge_Draw(bA,bC):
    P_2,l_2,E_2,I_2=1,1,1,1   # ←←←適当に?書いてます。
    b_1=Beam(  l_2,E_2,I_2)
    b_2=Beam(2*l_2,E_2,I_2)
    b_1.join(b_2,"hinge")
    b_1.apply_load   (P_2,l_2/3,-1)
    b_1.apply_support(  0  ,"fixed")
    b_1.apply_support(3*l_2,"fixed")
    b_1.draw().show()
    return 
my_Hinge_Draw(bA,bC)

ver0.4

・以下、間違っています。 ver0.4

# 以下、間違っています。 ver0.4
# ver0.4
from sympy.physics.continuum_mechanics.beam import Beam
from sympy import *
var('P,EI,x')             
var('PA,RA,MA')         
var('PC,RC,MC')         
var('l',positive=True)    # positive が,あればいいです。
# ----------------------------------------------------------
def my_Hinge_Def():
    var('n,m')
    bA=Beam(  l,  E,  I)
    bB=Beam(2*l,n*E,m*I)
    b =bA.join(bB,"hinge")
    b.apply_load(RA,  0,-1)
    b.apply_load(MA,  0,-2)
    b.apply_load(P ,  l,-1)
    b.apply_load(RC,3*l,-1)
    b.apply_load(MC,3*l,-2)
    b.bc_slope     =[(0,0),(3*l,0)]
    b.bc_deflection=[(0,0),(3*l,0)]
    b.solve_for_reaction_loads(RA,MA,RC,MC)
    sol=solve([Eq(b.reaction_loads[RA]/b.reaction_loads[RC],4), \
              Eq(n*m,2) \
              ],        \
              [n,m])[1]
    # ------------------------------------------------------------
    bA=Beam(  l,       E,       I)
    bB=Beam(2*l,sol[0]*E,sol[1]*I)
    b =bA.join(bB,"hinge")
    b.apply_load(RA,  0,-1)
    b.apply_load(MA,  0,-2)
    b.apply_load(P ,  l,-1)
    b.apply_load(RC,3*l,-1)
    b.apply_load(MC,3*l,-2)
    b.bc_slope     =[(0,0),(3*l,0)]
    b.bc_deflection=[(0,0),(3*l,0)]
    b.solve_for_reaction_loads(RA,MA,RC,MC)
    print("#",(sol[0]*E*sol[1]*I).simplify())
    print("#",b.reaction_loads[RA]/b.reaction_loads[RC])
    # 2*E*I
    # 4
    return b
def my_Hinge_Draw():
    P_2,l_2,E_2,I_2=1,1,1,1   # ←←←適当に?書いてます。
    bA=Beam(  l_2,E,I)
    bB=Beam(2*l_2,E,I)
    b_2 =bA.join(bB,"hinge")
    b_2.apply_load   (P_2,l_2,-1)
    b_2.apply_support(  0  ,"fixed")
    b_2.apply_support(3*l_2,"fixed")
    b_2.draw().show()
    return 
my_Hinge_Def()
my_Hinge_Draw()

いつもの? sympyの実行環境と 参考のおすすめです。

(テンプレート)

いつもと違うおすすめです。

sympyのdoc

・join(beam, via='fixed')