- ポケモン×データサイエンス(1) - ポケモン剣盾のランクバトルデータを解析してTableau上で可視化してみた
- ポケモン×データサイエンス(2) - ポケモン剣盾のパーティ構築をネットワーク分析から考える 試行編
- 【今回】ポケモン×データサイエンス(3) - ポケモン剣盾のパーティ構築をネットワーク分析から考える ネットワークの中心はどこ編
こんにちは、今回も前回の記事に引き続きグラフ理論、ネットワーク分析を扱っていきます。
前回の記事ではポケモン剣盾のランクバトルのパーティにおけるネットワークを可視化しました。今回は実際に分析にとりかかろうと思います。
今回使用したコード及びデータはこちらのGithubリポジトリにあります。
コード全文はこちら
今回実現したいこと
タイトルにある通り、ポケモン剣盾のパーティ構築ネットワークの各ノードクラスタリングしたいと思います。また、クラスタリングする前に中心性という概念を導入することで、重要ノードを捕捉したいと思います。
こんなものができていれば目標達成です。
ネットワークにおける中心
ネットワーク理論(グラフ理論)には中心性というものがあります。
中心性は、ネットワークにおける各頂点の重要性を評価したり、比較したりするための指標である。
各ノードがネットワーク内でどれだけ中心的=重要であるかを数学的に導出しようとした試みです。
今回はこの理論を用いて、各ノードのネットワークにおける重要性を算出してみたいと思います。
ですがこの中心性には、実はいろいろ種類があります。
1. 次数中心性
一つ目の中心性は次数中心性です。
次数とはノードのもつエッジの数です。次数の多さがそのまま中心性になります。
繋がっているノードが多いほど重要である!という考えに基づいた基本的な中心性である一方で、たびたび直感とずれた結果になることも多いように感じます。
2. 近接中心性, 離心中心性
続いては他のノードとの距離から中心性を導出する近接中心性、離心中心性です。
ネットワークの中央に近いほど重要である!という考えですね。
近接中心性は自ノードから他ノードまでの総距離の逆数を取り、離心中心性は自ノードから他ノードまでの距離の最大値の逆数を取ります。
距離を用いる両者の結果は非常に似通ったものになるので、今回は近接中心性を用いたいと思います。
3. 媒介中心性
一般に最もよく使われている(と思う)のは媒介中心性でしょう。
簡単に言えば最短経路上に頻繁に位置しているものほど重要であるという考え方(中継性)です。
コミュニティのネットワークにおける媒介中心性が高いノードというのは、そのノードを経由しなければ、別のコミュニティにアクセスすることができないような立ち位置にいるということであり、直感的に重要そうであるということが分かっていただけるのではないでしょうか。
4. 固有ベクトル中心性
固有ベクトル中心性は今まで紹介してきた4つの中心性とは大きく違い、「どのノードと繋がっているか」という考えを導入した中心性になります。
「重要なノードと繋がているノードはより重要である」という考えを取り入れ、自分と繋がる他人の中心性を足し合わせる処理を反復し、収束した値を中心性とします。
5. ページランク
Google創業者ラリー・ペイジとセルゲイ・ブリンが考案した中心性です。
基本的な考え方は固有ベクトル中心性と同じです。どこが違うかを理解するには、固有ベクトル中心性の問題点を知る必要があります。
ネットワーク中に、他のノードからエッジを1つも貼られていないノードがあったとします。このノードの中心性は勿論0です。ここまでは良いのですが、次が少々厄介です。このようなノードのみと繋がったノードiがあったとします。当然繋がっているノードから中心性が遷移してこないのでiの中心性も0となってしまいます。これは直感に反すると思います。
また、途轍もなく大きな中心性を持ったノードjと繋がったノードiがあったとしましょう。固有ベクトル中心性の考え方では、ノードiにはノードjの中心性が遷移してくる訳ですが、ノードiはノードjがエッジを貼る数多くあるノードのうちの1つに過ぎません。ノードiに対してノードjが持つ中心性の全てを遷移すべきでしょうか?
このような諸問題をある程度解決した中心性指標がページランクなのです。
Googleの検索アルゴリズムの基礎となり、今も論文のインパクトファクターの算出などに使用されているそうです。
中心性の導出
中心性の導出にあたって使用するデータは前回から引き続き、ポケモン剣盾のランクバトルの”一緒に採用されるポケモンランキング”データと採用ランキングデータです。
採用ランキング上位の100匹で構成されたネットワークを対象に分析を行います。
df = pd.read_csv(FILEPATH_TEMOTI_POKEMON), encoding='utf-8')
df_rank = pd.read_csv(FILEPATH_ADO_RANK, encoding='utf-8')
df.columns = ['Season', 'Rule', 'Pokemon_From', 'Pokemon_To', 'Weight']
df['Weight'] = 10-df['Weight']
df_season11_double = df[(df['Season']==11)&(df['Rule']=='Double')]
df_season11_double = df_season11_double.drop(['Season', 'Rule'], axis=1)
# 採用率上位100匹に限定
df_season11_double = df_season11_double[df_season11_double['Pokemon_From'].isin(list(df_rank['Pokemon'])[:100])]
df_season11_double = df_season11_double[df_season11_double['Pokemon_To'].isin(list(df_rank['Pokemon'])[:100])]
df_season11_double.to_csv(OUTPUT_FILEPATH', index=False)
df_season11_double
| index | Pokemon_From | Pokemon_To | Weight |
|---|---|---|---|
| 91394 | リザードン | キュウコン | 9 |
| 91395 | リザードン | トリトドン | 8 |
| 91396 | リザードン | ピッピ | 7 |
| 91397 | リザードン | テラキオン | 6 |
| 91398 | リザードン | ヤミラミ | 5 |
| 504 rows × 3 columns |
上記で作成したデータからネットワークをつくります。
import networkx as nx
network_np = df_season11_double.values
G = nx.DiGraph()
G.add_weighted_edges_from(network_np)
1. 次数中心性
degree_centers = nx.degree_centrality(G)
df_dc = pd.DataFrame(sorted(degree_centers.items(), key=lambda x: x[1], reverse=True), columns=['Pokemon', 'Degree centrality'])
df_dc.head(10)
| index | Pokemon | Degree centrality |
|---|---|---|
| 0 | ウーラオス | 0.500000 |
| 1 | ファイアロー | 0.490291 |
| 2 | アシレーヌ | 0.451456 |
| 3 | モロバレル | 0.419903 |
| 4 | ウインディ | 0.359223 |
| 5 | サマヨール | 0.308252 |
| 6 | オーロンゲ | 0.293689 |
| 7 | ラプラス | 0.291262 |
| 8 | リザードン | 0.269417 |
| 9 | ナットレイ | 0.237864 |
2. 近接中心性
close_centers = nx.closeness_centrality(G)
df_cc = pd.DataFrame(sorted(close_centers.items(), key=lambda x: x[1], reverse=True), columns=['Pokemon', 'Closeness centrality'])
df_cc.head(10)
| index | Pokemon | Closeness centrality |
|---|---|---|
| 0 | ウーラオス | 0.648440 |
| 1 | ファイアロー | 0.646345 |
| 2 | アシレーヌ | 0.628081 |
| 3 | モロバレル | 0.612691 |
| 4 | ウインディ | 0.594483 |
| 5 | サマヨール | 0.572371 |
| 6 | ラプラス | 0.562711 |
| 7 | オーロンゲ | 0.551085 |
| 8 | ピッピ | 0.545078 |
| 9 | ナットレイ | 0.545078 |
3. 媒介中心性
between_centers = nx.betweenness_centrality(G)
df_bc = pd.DataFrame(sorted(between_centers.items(), key=lambda x: x[1], reverse=True), columns=['Pokemon', 'Betweenness centrality'])
df_bc.head(10)
| index | Pokemon | Betweenness centrality |
|---|---|---|
| 0 | キュウコン | 0.046012 |
| 1 | ペルシアン | 0.036945 |
| 2 | トリトドン | 0.028901 |
| 3 | リザードン | 0.025690 |
| 4 | テラキオン | 0.021207 |
| 5 | グレイシア | 0.019807 |
| 6 | サンドパン | 0.018529 |
| 7 | アシレーヌ | 0.013435 |
| 8 | ニャイキング | 0.011381 |
| 9 | エレザード | 0.009867 |
4. 固有ベクトル中心性
eigen_centers = nx.eigenvector_centrality_numpy(G)
df_ec = pd.DataFrame(sorted(eigen_centers.items(), key=lambda x: x[1], reverse=True), columns=['Pokemon', 'Eigen centrality'])
df_ec.head(10)
| index | Pokemon | Eigen centrality |
|---|---|---|
| 0 | ウーラオス | 0.374252 |
| 1 | アシレーヌ | 0.362932 |
| 2 | ファイアロー | 0.341690 |
| 3 | モロバレル | 0.332555 |
| 4 | サマヨール | 0.297832 |
| 5 | ウインディ | 0.292263 |
| 6 | パッチラゴン | 0.261000 |
| 7 | ナットレイ | 0.259066 |
| 8 | ピッピ | 0.237895 |
| 9 | ラプラス | 0.218322 |
5. ページランク
pageranks = nx.pagerank(G)
df_pr = pd.DataFrame(sorted(pageranks.items(), key=operator.itemgetter(1),reverse = True), columns=['Pokemon', 'Page Rank'])
df_pr.head(10)
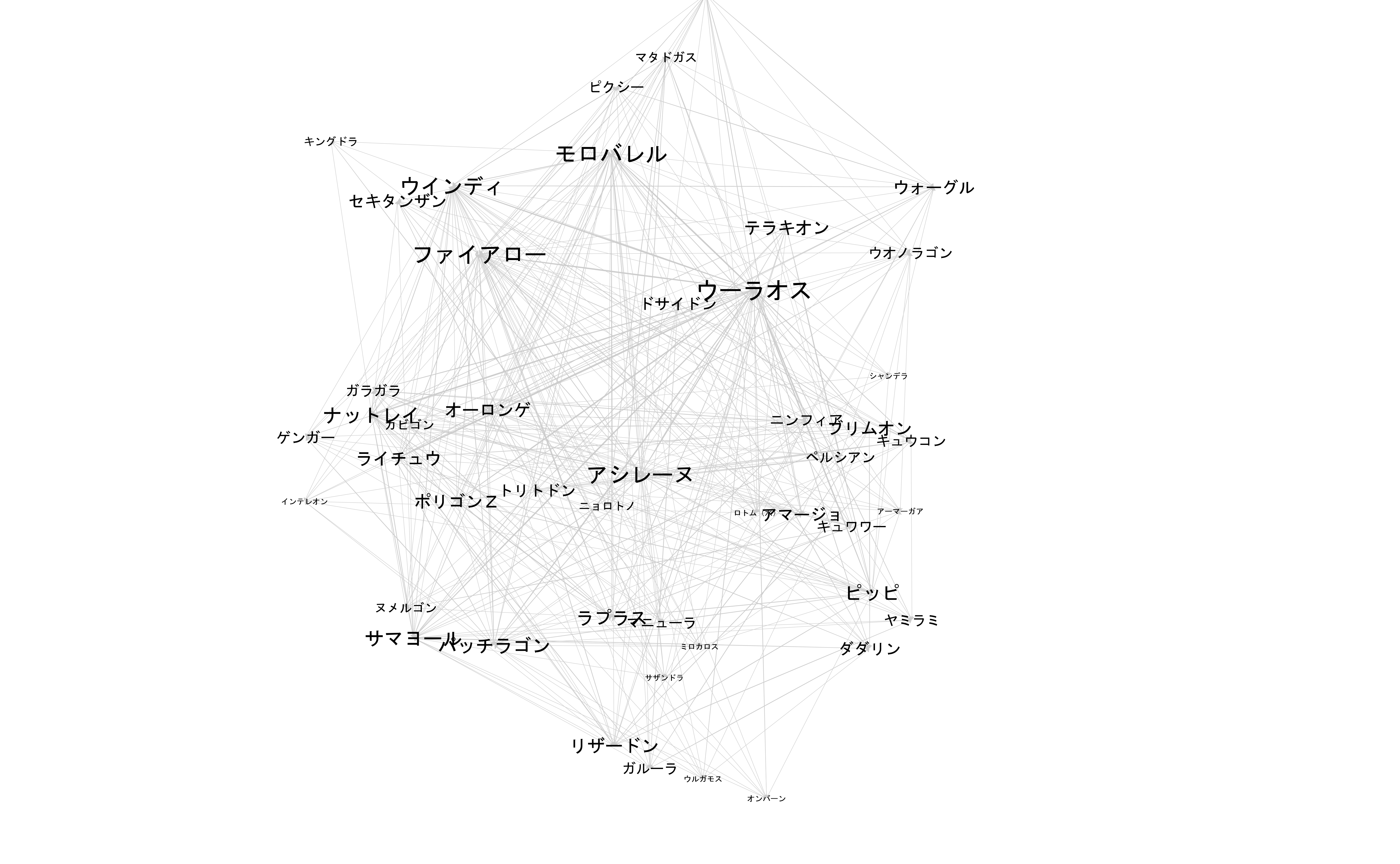
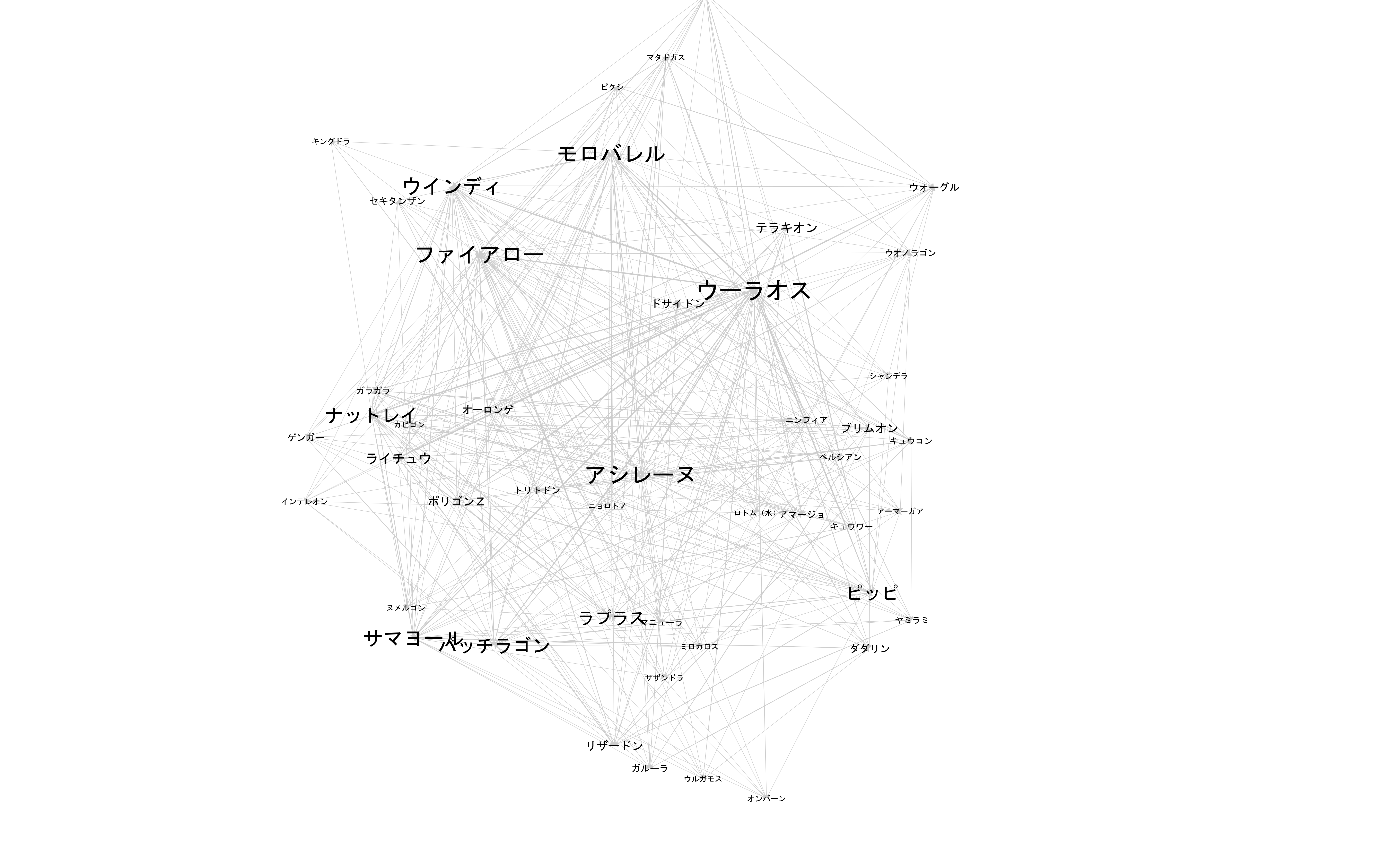
※他の中心性の図とノードの位置が違いますが同一のネットワークです。
中心性が大きいノードのラベルフォントを大きくしてみました。
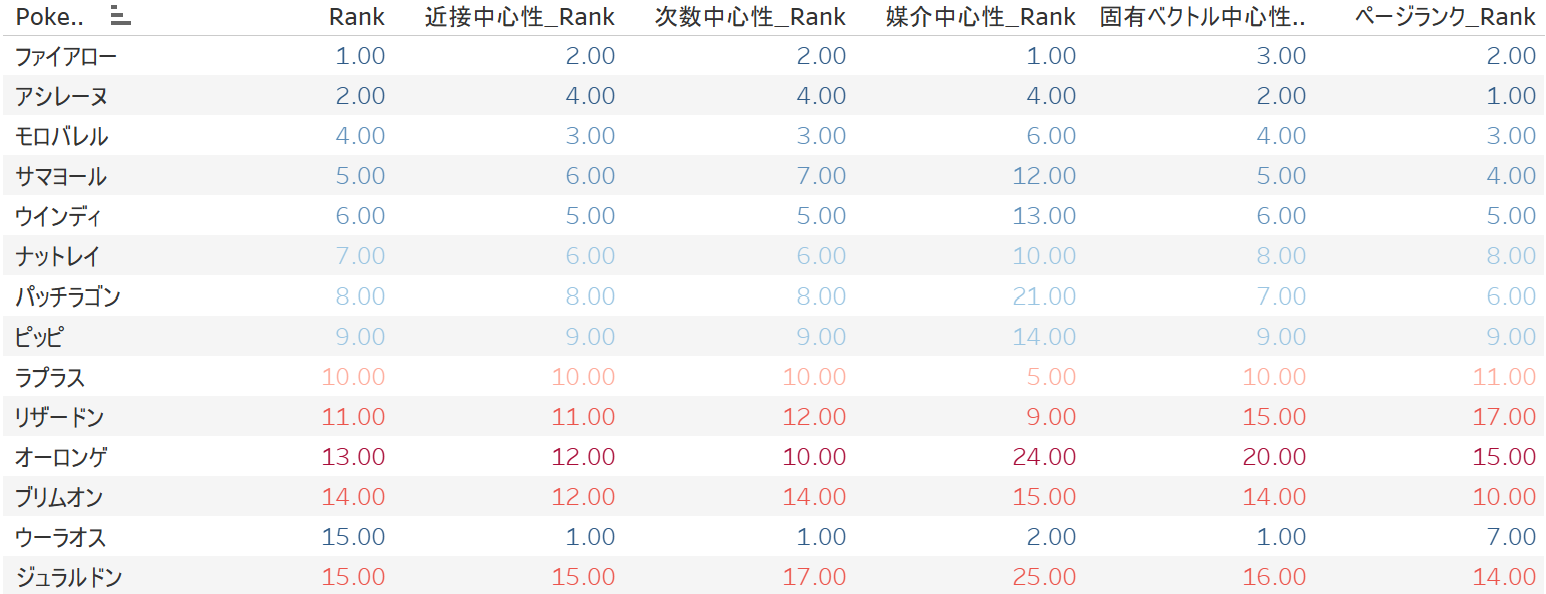
公開されているランキングと各中心性指標を並べてみました。
上位100匹かつ併用ランク上位10匹に絞ったランキングにおいては、どの指標においても、ウーラオスが顕著に公開されているランクよりも高いことが分かります。(過大評価されてしまっている感)
以降では、ページランクを使用します。
ネットワーク構造のクラスタリング
いよいよ大詰めです。今回の主題であるネットワーク構造のクラスタリングに入りたいと思います。
クラスタリング(コミュニティ抽出)手法は、先ほど導出した媒介中心性・固有ベクトル中心性などを使ったものや今回紹介していない情報中心性、スピングラス法、ランダムウォークなど多種多様な手法があります。
今回は中心性の導出にかなりの文量を割いてしまったので、各中心性によるクラスタリングの実行・結果の比較はまた別の機会に譲りたいと思います。
取り急ぎ今回は。こちら(論文, 実装ライブラリ)の手法を用いてクラスタリングしていきます。
この手法はネットワークの密集度の指標(モジュラリティ)が最大になるように分割する手法であり、事前にクラスター数を指定する必要がない点でk-meansと違いがあります。
この実装では有向グラフは使用できないので、無向グラフに変換を行います。
# 有向グラフを無向グラフに変換
G2 = nx.Graph(G)
import community
partition = community.best_partition(G2)
partition2 = {}
for i in partition.keys():
sub_dict = {'community' : partition[i]}
partition2[i] = sub_dict
labels = dict([(i, str(i)) for i in range(nx.number_of_nodes(G2))])
labels2 = {}
for i in range(len(labels)):
sub_dict = {'labels' : labels[i]}
labels2[list(partition.keys())[i]] = sub_dict
nx.set_node_attributes(G2, labels2)
nx.set_node_attributes(G2, partition2)
nx.write_gml(G2, ".//community.gml")
pd.DataFrame.from_dict(labels2).T.to_csv('.//community_labels.csv')
クラスターの解釈
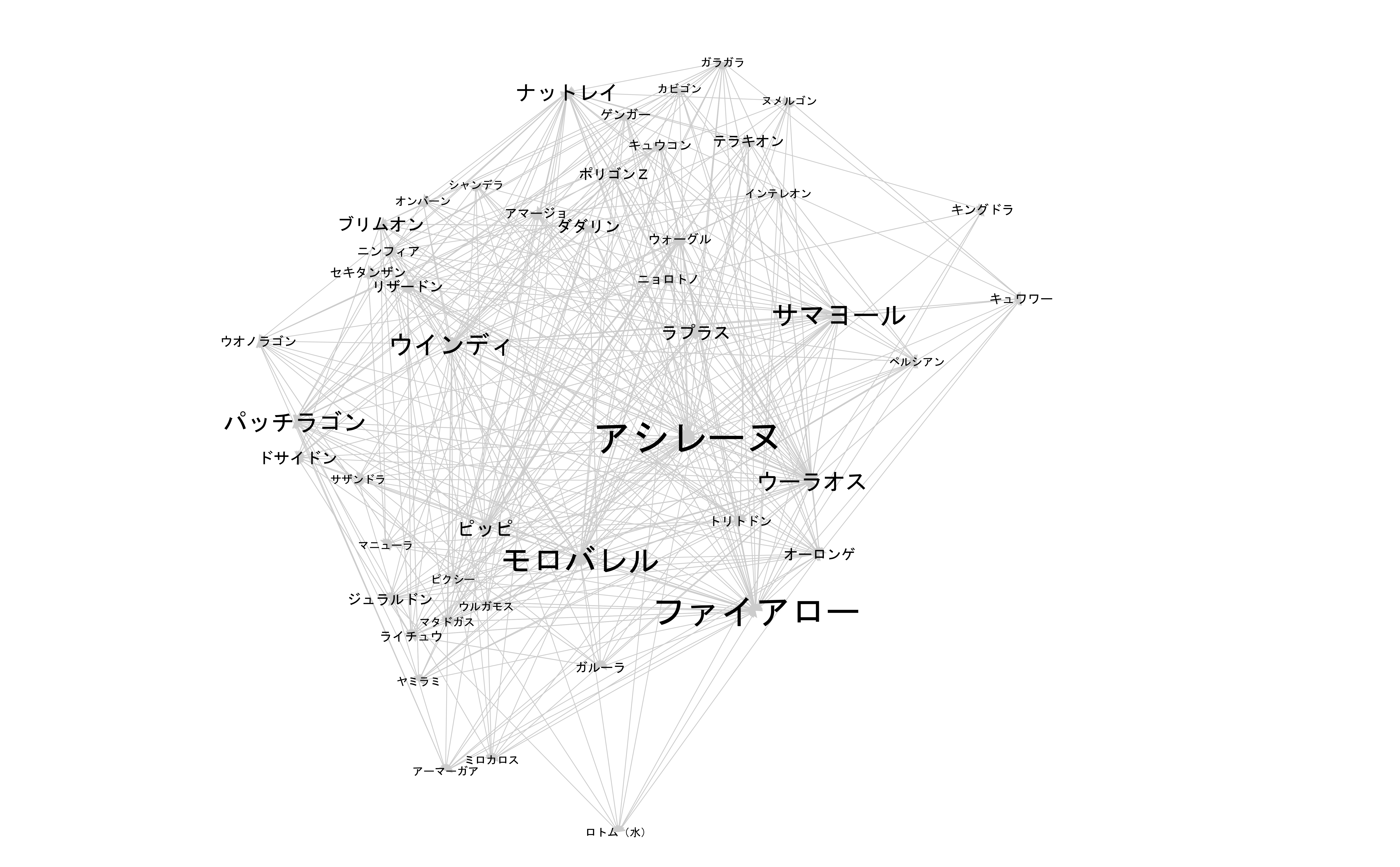
クラスタリングの結果、6クラスターが抽出されました。各クラスターについて見ていきましょう。
df_pagerank = pd.DataFrame(sorted(pageranks.items(), key=operator.itemgetter(1),reverse = True), columns=['Pokemon', 'Page Rank'])
df_community = pd.concat([pd.DataFrame.from_dict(labels2).T, pd.DataFrame.from_dict(partition2).T], axis=1)
df_community = df_community.reset_index()
df_community.columns = ['Pokemon', 'label', 'community']
df_pagerank_community = pd.merge(left=df_pagerank, right=df_community, on = 'Pokemon')
各クラスターに分類されたポケモンの下図を確認します。
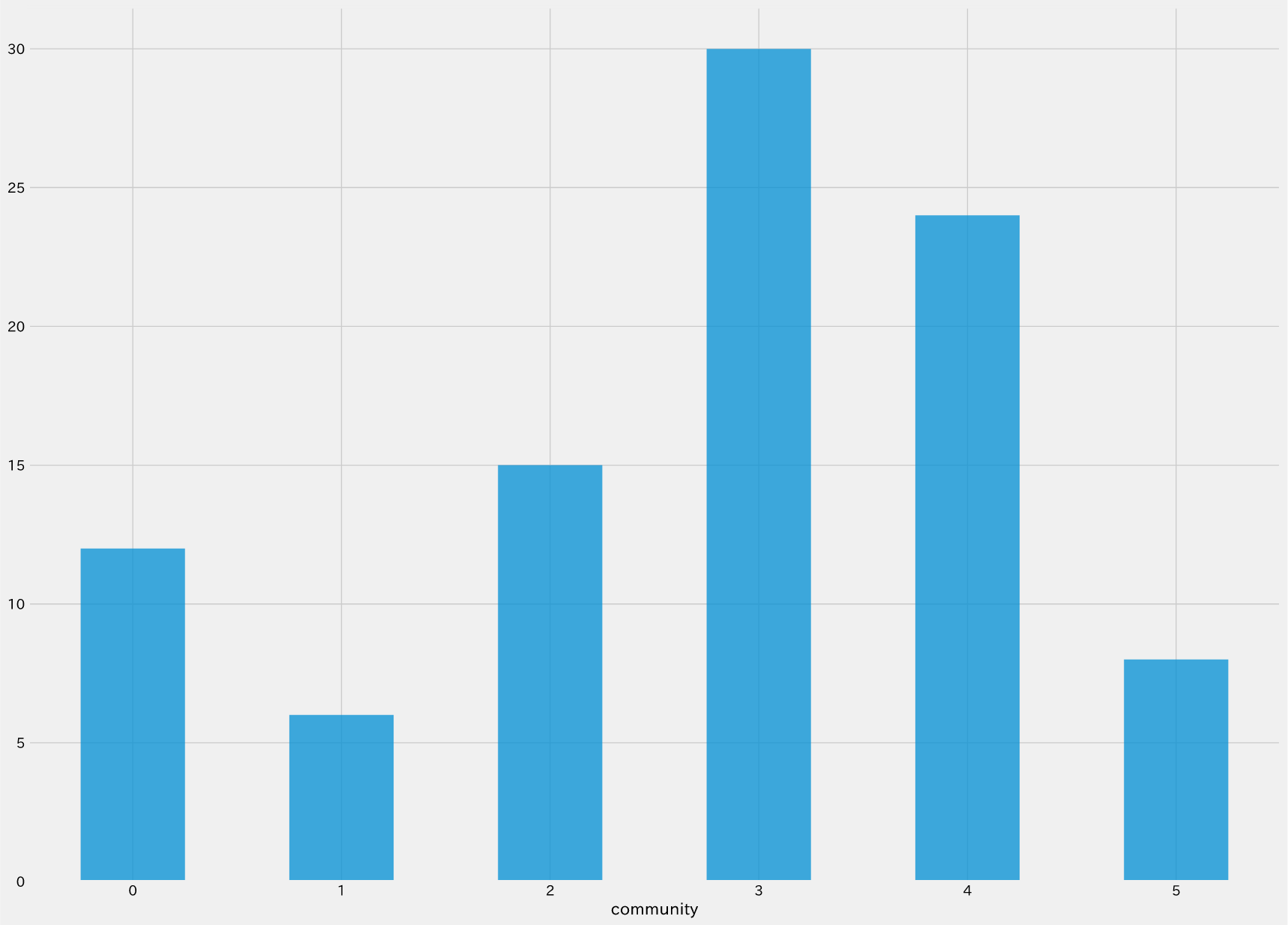
df_pagerank_community.groupby('community').count()['Pokemon'].plot.bar(rot=0, alpha=0.75)
クラスター3が全体の30%近くを占めていることが分かります。
それでは各クラスターの中身を見ていきましょう。
クラスター0
df_pagerank_community[df_pagerank_community['community']==0].head(10)
| index | Pokemon | Page Rank | label | community |
|---|---|---|---|---|
| 13 | リザードン | 0.013742 | 0 | 0 |
| 18 | トリトドン | 0.007309 | 2 | 0 |
| 19 | セキタンザン | 0.006604 | 32 | 0 |
| 20 | キュウコン | 0.006319 | 1 | 0 |
| 30 | ヤミラミ | 0.002842 | 5 | 0 |
| 42 | マニューラ | 0.001501 | 68 | 0 |
| 46 | ニューラ | 0.001235 | 55 | 0 |
| 53 | コバルオン | 0.001133 | 56 | 0 |
| 61 | リーフィア | 0.000935 | 30 | 0 |
| 69 | ビリジオン | 0.000789 | 69 | 0 |
リザードン・キュウコンを中心とした晴れパでしょうか。中心性の1位はリザードン、2位にはリザードンとの相性補完に優れたトリトドンがランクインしています。
クラスター1
df_pagerank_community[df_pagerank_community['community']==1].head(10)
| index | Pokemon | Page Rank | label | community |
|---|---|---|---|---|
| 8 | ピッピ | 0.033903 | 3 | 1 |
| 16 | ポリゴンZ | 0.012646 | 27 | 1 |
| 17 | テラキオン | 0.009129 | 4 | 1 |
| 41 | ペルシアン | 0.001544 | 33 | 1 |
| 80 | レントラー | 0.000630 | 64 | 1 |
| 81 | エンニュート | 0.000629 | 92 | 1 |
続いてクラスター1はこちらの6匹でした。サポート性能が非常に高い輝石ピッピや適応力ダイマックスにより超火力を出せるポリゴンZが分類されました。所感としてはどのようなパーティにも活躍できる汎用性の高いポケモンが名を連ねているイメージです。
クラスター2
df_pagerank_community[df_pagerank_community['community']==2].head(10)
| index | Pokemon | Page Rank | label | community |
|---|---|---|---|---|
| 7 | ナットレイ | 0.038186 | 6 | 2 |
| 24 | ニンフィア | 0.005511 | 20 | 2 |
| 28 | ペリッパー | 0.003061 | 57 | 2 |
| 29 | ウオノラゴン | 0.002859 | 46 | 2 |
| 32 | キングドラ | 0.002468 | 49 | 2 |
| 33 | ニョロトノ | 0.002321 | 47 | 2 |
| 35 | ルンパッパ | 0.002233 | 50 | 2 |
| 37 | ガマゲロゲ | 0.001736 | 58 | 2 |
| 38 | シュバルゴ | 0.001626 | 59 | 2 |
| 39 | マタドガス | 0.001572 | 44 | 2 |
クラスター2は分かりやすいですね、ペリッパー、キングドラ、ルンパッパなどが含まれる雨パです。水タイプとの相性補完に優れるナットレイの中心性が高くなっています。また、シュバルゴなど炎タイプを苦手するポケモンが雨パと構成されていることも直感と一致しています。
クラスター3
df_pagerank_community[df_pagerank_community['community']==3].head(10)
| index | Pokemon | Page Rank | label | community |
|---|---|---|---|---|
| 0 | アシレーヌ | 0.107503 | 7 | 3 |
| 1 | ファイアロー | 0.093996 | 12 | 3 |
| 4 | ウインディ | 0.056541 | 15 | 3 |
| 5 | パッチラゴン | 0.049160 | 16 | 3 |
| 14 | ジュラルドン | 0.013730 | 24 | 3 |
| 15 | オーロンゲ | 0.013617 | 29 | 3 |
| 21 | アマージョ | 0.006167 | 17 | 3 |
| 26 | ウォーグル | 0.003980 | 23 | 3 |
| 27 | ゲンガー | 0.003799 | 43 | 3 |
| 34 | ピクシー | 0.002254 | 28 | 3 |
クラスター3は環境トップメタが集中しているように見えます。ネット上に転がっているパーティ構築考察を参照すると、結果を残した構築としてしばしばアシレーヌ・ファイアロー・パッチラゴンの組み合わせが散見されますので、シーズン11ダブル環境において大きな影響力を有していたポケモン達が多いのではないかと推察します。
クラスター4
df_pagerank_community[df_pagerank_community['community']==4].head(10)
| index | Pokemon | Page Rank | label | community |
|---|---|---|---|---|
| 2 | モロバレル | 0.083762 | 8 | 4 |
| 3 | サマヨール | 0.061276 | 9 | 4 |
| 9 | ブリムオン | 0.026956 | 25 | 4 |
| 11 | ドサイドン | 0.016228 | 21 | 4 |
| 12 | ダダリン | 0.014804 | 26 | 4 |
| 22 | ライチュウ | 0.006124 | 13 | 4 |
| 25 | ガルーラ | 0.005487 | 19 | 4 |
| 31 | ガラガラ | 0.002758 | 39 | 4 |
| 40 | ヤドラン | 0.001563 | 40 | 4 |
| 45 | ストリンダー | 0.001322 | 82 | 4 |
こちらのクラスターも非常に分かりすいですね。トリル起動役のサマヨールやブリムオン、トリルアタッカーとなるドサイドン、ダダリン、ガラガラ、サポート役のモロバレルが分類されています。
中心性を見ると、モロバレルが非常に重要な役割を果たしていることが分かります。
クラスター5
df_pagerank_community[df_pagerank_community['community']==5].head(10)
| index | Pokemon | Page Rank | label | community |
|---|---|---|---|---|
| 6 | ウーラオス | 0.045935 | 10 | 5 |
| 10 | ラプラス | 0.024565 | 22 | 5 |
| 23 | キュワワー | 0.005706 | 14 | 5 |
| 36 | ヌメルゴン | 0.002140 | 88 | 5 |
| 50 | オンバーン | 0.001201 | 83 | 5 |
| 55 | カメックス | 0.001056 | 11 | 5 |
| 63 | マホイップ | 0.000880 | 94 | 5 |
| 90 | トゲデマル | 0.000463 | 93 | 5 |
最後のクラスターはこちらの8匹となりました。このポケモンたちはどういう集まりなのでしょうか。私の知識集合では解釈が難しかったため、コメントにてお待ちしております。
可視化
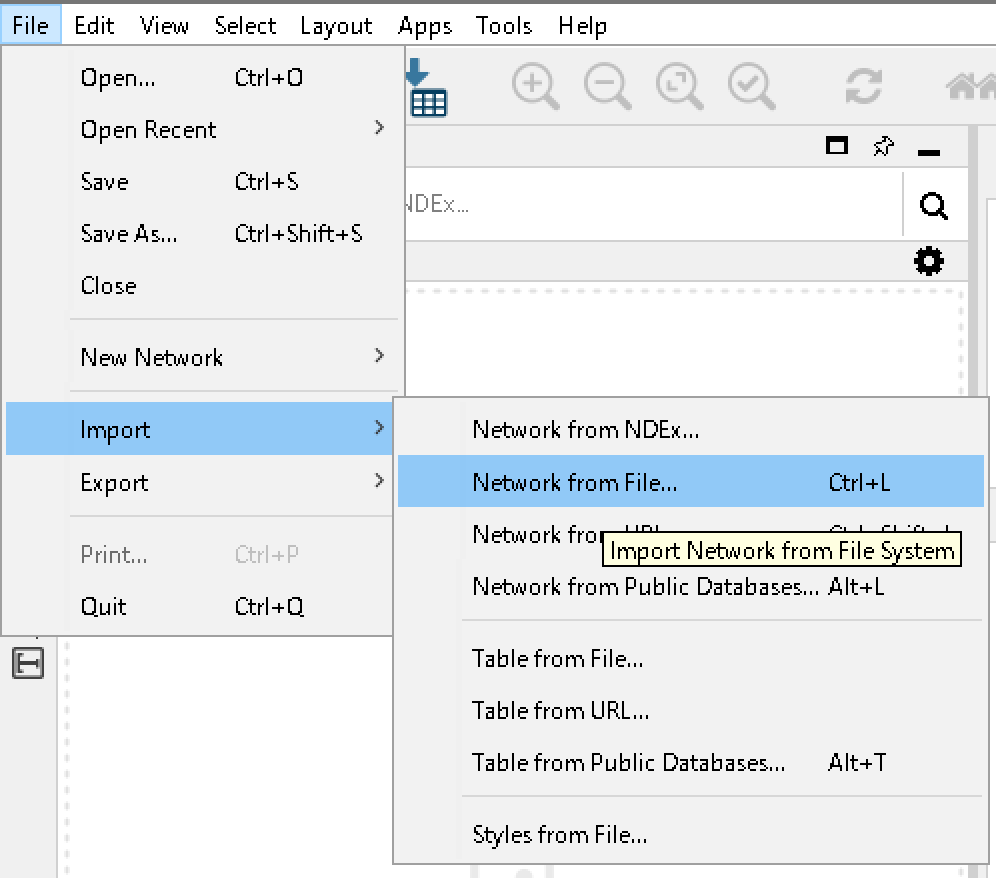
最後に前回使い方を確認したCytoscapeにてネットワークを可視化します。
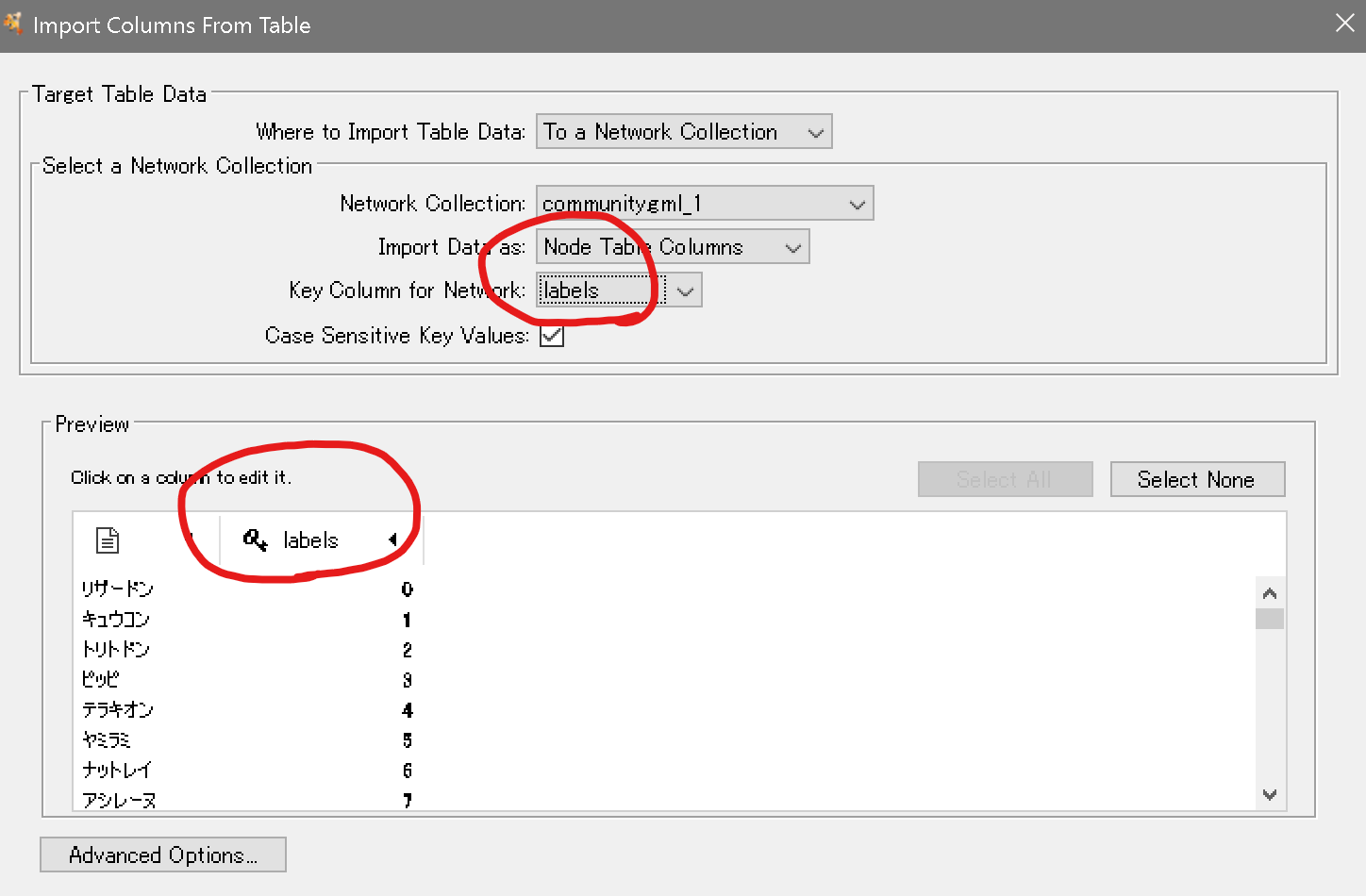
File > Import > Network from File から community.gmlを読み込み、上部のImport Table from File(下図参照)
から、community_labels.csvを読み込み、表示されたダイアログボックスを以下のように設定します。
赤の部分はデフォルトから変更する必要があるので注意です。
あとはStyleタブからContinuous Mappingを駆使してクラスター毎に形状や色を変更していくだけです。
試しにフォント色をクラスター、フォントサイズをページランクとしてネットワークを可視化してみました。
次回はこのデータに最適なクラスタリング手法の探索なんかをやってみたいと思います。
それではまた。
出典等
- ポケモン×データサイエンス(1) - ポケモン剣盾のランクバトルデータを解析してTableau上で可視化してみた
- ポケモン×データサイエンス(2) - ポケモン剣盾のパーティ構築をネットワーク分析から考える 試行編
- Cytoscape.org
- Fast unfolding of communities in large networks
- モジュラリティ
©2020 Pokémon ©1995-2020 Nintendo/Creatures Inc./GAME FREAK inc. ポケットモンスター・ポケモン・Pokémonは任天堂・クリーチャーズ・ゲームフリークの登録商標です。