Pythonで体験するベイズ推論より
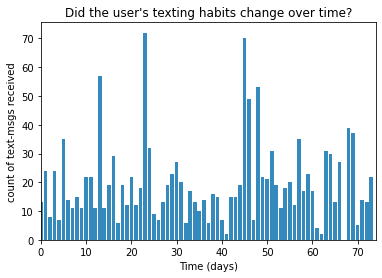
メッセージ数に変化はあったのか?
ここで実際に例題を計算します。
Pythonのスクリプトは、書籍はPyMC2で書いてあるけど、私の理解の範疇で、公式HPのPyMC3のスクリプトをもとに書いています。
あるユーザーが毎日受信するメッセージ数があった時に、この受信メッセージ数に変化点があったかどうか?ということである。
データは、公式githubから入手ください。
# -*- coding: utf-8 -*-
# データの可視化
from matplotlib import pyplot as plt
import numpy as np
count_data = np.loadtxt("data/txtdata.csv")
n_count_data = len(count_data)
plt.bar(np.arange(n_count_data), count_data, color="#348ABD")
plt.xlabel("Time (days)")
plt.ylabel("count of text-msgs received")
plt.title("Did the user's texting habits change over time?")
plt.xlim(0, n_count_data)
plt.show()
これが、どこかに変化があるとわかるだろうか?グラフを見ただけではわかりません。
どう考えるかというと、
ベイズ推論の考え方・・「ベイズ主義と確率分布」
まず、これは毎日の受信数になるので、離散値のデータになります。だからポアソン分布になります。
そこで。$i$日目のメッセージ数を$C_i$とすると、
C_i \sim \text{Poisson}(\lambda)
ここで$λ$をどう考えるかというと、この期間内にどこかで$λ$が変わったかもしれないと考えます。
これを$τ$日目にパラメーター$λ$が変わったと考える。
この急激に変わった点を、変化点(switchpoint)という。
$λ$を次のようにあらわす。
\lambda =
\begin{cases}
\lambda_1 & \text{if } t \lt \tau \cr
\lambda_2 & \text{if } t \ge \tau
\end{cases}
もしメールの受信数が変化がない場合は、$\lambda_1 = \lambda_2$となるはずである。
さてこの$λ$を考えるために、指数分布でモデル化することとする。(だって$λ$は連続値だから)
この時のパラメーターを$α$とすると、次の式で表される。
\begin{align}
&\lambda_1 \sim \text{Exp}( \alpha ) \\\
&\lambda_2 \sim \text{Exp}( \alpha )
\end{align}
指数分布の期待値は、パラメーターの逆数なので、次で表される。
\frac{1}{N}\sum_{i=0}^N \;C_i \approx E[\; \lambda \; |\; \alpha ] = \frac{1}{\alpha}
これで事前分布には主観が入らない。ここで、2つの$\lambda_i$に違う事前分布を使うと、観測期間中にどこかで受信数に変化が表れたと考えているという信念を表している。
後、$τ$をどう考えるかというと、$τ$は一様分布(uniform distribution)を使うことにする。つまりどの日も同等であるという信念である。
\begin{align}
& \tau \sim \text{DiscreteUniform(1,70) }\\\\
& \Rightarrow P( \tau = k ) = \frac{1}{70}
\end{align}
ここまでくると、これをどうpythonでプログラムを書くか迷うが、後はpymc3で書き表すことになる。
hon
import pymc3 as pm
import theano.tensor as tt
with pm.Model() as model:
alpha = 1.0/count_data.mean()
# Recall count_data is the
# variable that holds our txt counts
lambda_1 = pm.Exponential("lambda_1", alpha)
lambda_2 = pm.Exponential("lambda_2", alpha)
tau = pm.DiscreteUniform("tau", lower=0, upper=n_count_data - 1)
lambda_1 = pm.Exponential("lambda_1", alpha)
$\lambda_1$と$\lambda_2$に対応するPyMC変数を作る。
tau = pm.DiscreteUniform("tau", lower=0, upper=n_count_data - 1)
$\tau$を一様分布pm.DiscreteUniformで与える。
with model:
idx = np.arange(n_count_data) # Index
lambda_ = pm.math.switch(tau > idx, lambda_1, lambda_2)
with model:
observation = pm.Poisson("obs", lambda_, observed=count_data)
lambda_ = pm.math.switch(tau > idx, lambda_1, lambda_2)
ここで、新しいlambda_を作ります。
switch()関数は、tauのどちら側にいるかに応じて、lambda_1の値またはlambda_2をlambda_の値として割り当てます。 tauまでのlambda_の値はlambda_1で、それ以降の値はlambda_2になります。
observation = pm.Poisson("obs", lambda_, observed=count_data)
ここは、データcount_dataを、変数lambda_によって提供される変数により計算し、観測されるということになっているということです。
with model:
step = pm.Metropolis()
trace = pm.sample(10000, tune=5000,step=step, cores=1)
lambda_1_samples = trace['lambda_1']
lambda_2_samples = trace['lambda_2']
tau_samples = trace['tau']
このコードの詳細は書籍では第3章になるようです。ここが学習ステップで、マルコフ連鎖モンテカルロ(MCMC)と呼ばれるアルゴリズムで計算しています。これは、トレースと呼ばれる$\lambda_1$$\lambda_2$$\tau$の事後分布から数千の確率変数を戻します。
この確率変数をプロットすることにより、事後分布の形を見ることができます。
ここで計算が始まりますが、マルチコアやCudaが使えない(cores=1)ので、非常に時間がかかりますが答えは出ます。
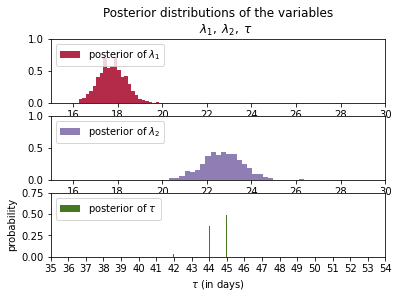
結果を見てわかるように、
$\lambda_1=18$
$\lambda_2=23$
$\tau=45$
$\tau$が45日が多く、その確率が50%になっている。
つまり理由はわからないが、45日目前後に、何かの変化(受信数を変える何かの行動・・でもこれは本人しかわからない)があり、$\lambda$が変わっている。
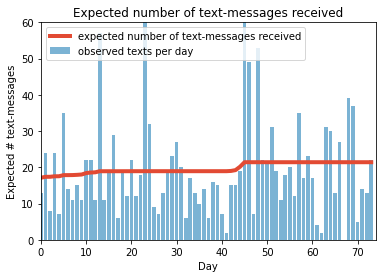
最後に受信数の期待値を書いてみます。
このように、ベイズ推定を使うと、データから、いつ変化点があったかがわかります。
しかし注意する点は、この受信数の期待値も実際には分布になっている点です。また、原因は自分自身で考える必要があります。
最後に全部のスクリプトです。
# -*- coding: utf-8 -*-
# データの可視化
from matplotlib import pyplot as plt
import numpy as np
count_data = np.loadtxt("data/txtdata.csv")
n_count_data = len(count_data)
plt.bar(np.arange(n_count_data), count_data, color="#348ABD")
plt.xlabel("Time (days)")
plt.ylabel("count of text-msgs received")
plt.title("Did the user's texting habits change over time?")
plt.xlim(0, n_count_data);
plt.show()
import pymc3 as pm
import theano.tensor as tt
with pm.Model() as model:
alpha = 1.0/count_data.mean()
# Recall count_data is the
# variable that holds our txt counts
lambda_1 = pm.Exponential("lambda_1", alpha)
lambda_2 = pm.Exponential("lambda_2", alpha)
tau = pm.DiscreteUniform("tau", lower=0, upper=n_count_data - 1)
with model:
idx = np.arange(n_count_data) # Index
lambda_ = pm.math.switch(tau > idx, lambda_1, lambda_2)
with model:
observation = pm.Poisson("obs", lambda_, observed=count_data)
### Mysterious code to be explained in Chapter 3.
with model:
step = pm.Metropolis()
trace = pm.sample(10000, tune=5000,step=step, cores=1)
lambda_1_samples = trace['lambda_1']
lambda_2_samples = trace['lambda_2']
tau_samples = trace['tau']
# histogram of the samples:
ax = plt.subplot(311)
ax.set_autoscaley_on(False)
plt.hist(lambda_1_samples, histtype='stepfilled', bins=30, alpha=0.85,
label="posterior of $\lambda_1$", color="#A60628", density=True)
plt.legend(loc="upper left")
plt.title(r"""Posterior distributions of the variables
$\lambda_1,\;\lambda_2,\;\tau$""")
plt.xlim([15, 30])
plt.xlabel("$\lambda_1$ value")
ax = plt.subplot(312)
ax.set_autoscaley_on(False)
plt.hist(lambda_2_samples, histtype='stepfilled', bins=30, alpha=0.85,
label="posterior of $\lambda_2$", color="#7A68A6", density=True)
plt.legend(loc="upper left")
plt.xlim([15, 30])
plt.xlabel("$\lambda_2$ value")
plt.subplot(313)
w = 1.0 / tau_samples.shape[0] * np.ones_like(tau_samples)
plt.hist(tau_samples, bins=n_count_data, alpha=1,
label=r"posterior of $\tau$",
color="#467821", weights=w, rwidth=2.)
plt.xticks(np.arange(n_count_data))
plt.legend(loc="upper left")
plt.ylim([0, .75])
plt.xlim([35, len(count_data)-20])
plt.xlabel(r"$\tau$ (in days)")
plt.ylabel("probability");
plt.show()
# tau_samples, lambda_1_samples, lambda_2_samples contain
# N samples from the corresponding posterior distribution
N = tau_samples.shape[0]
expected_texts_per_day = np.zeros(n_count_data)
for day in range(0, n_count_data):
# ix is a bool index of all tau samples corresponding to
# the switchpoint occurring prior to value of 'day'
ix = day < tau_samples
# Each posterior sample corresponds to a value for tau.
# for each day, that value of tau indicates whether we're "before"
# (in the lambda1 "regime") or
# "after" (in the lambda2 "regime") the switchpoint.
# by taking the posterior sample of lambda1/2 accordingly, we can average
# over all samples to get an expected value for lambda on that day.
# As explained, the "message count" random variable is Poisson distributed,
# and therefore lambda (the poisson parameter) is the expected value of
# "message count".
expected_texts_per_day[day] = (lambda_1_samples[ix].sum()
+ lambda_2_samples[~ix].sum()) / N
plt.plot(range(n_count_data), expected_texts_per_day, lw=4, color="#E24A33",
label="expected number of text-messages received")
plt.xlim(0, n_count_data)
plt.xlabel("Day")
plt.ylabel("Expected # text-messages")
plt.title("Expected number of text-messages received")
plt.ylim(0, 60)
plt.bar(np.arange(len(count_data)), count_data, color="#348ABD", alpha=0.65,
label="observed texts per day")
plt.legend(loc="upper left")
plt.show()