Pythonで体験するベイズ推論より
一回書いたけど、なんか馴れてないので、この項目消してしまいました。
そういうわけで、もう一回書いてます。。トホホ。
ベイズ主義とは
頻度主義とベイズ主義
頻度主義とは、昔からある古典的な統計学である。
頻度主義では、確率を「長期間における事象の頻度」とみなす.
ベイズ主義では、確率を「ある事象が発生する信念(belief)」あるいは「確信(confidence)」の度合いとみなす。
確率を信念とみなすことは、実は人間にとって自然な考え方である。
「確率とは信念である」
ある事象が生じる信念を$P(A)$と表し、事前確率と呼び、証拠$X$が与えられて更新された信念を$P(A|X)$と表す。これは証拠Xが与えられた時の$A$の確率である。これを事後確率と呼ぶ。
ベイズ推論の考え方
ベイズ主義の推論関数は確率を戻すが、頻度主義の推論関数は推定値を表す数値を戻す。。
これは重要なことなので、覚えておいた方が良い。
例えば、プログラムの例題を考えると、
頻度主義の考え方で「このプラグラムはすべてのテストにパスした。(情報X)このプラグラムに問題はないか?」と考えた場合、「はいプログラムにバグはありません」となるだろう。
これをベイズ主義で考えるとこう答える。
「はい、バグがない確率は0.8です。いいえ、バグがある確率は0.2です。」
ベイズ主義では、プログラムにはいつでもバグがあるという事前知識を引数として追加できる。
証拠(情報X)が多くなり無限個(非常に大きな)の証拠が集まると、結果として頻度主義とベイズ主義は似たような推論結果を出してくることになる。
ビッグデータについて
ビッグデータを利用した分析、予測は比較的単純なアルゴリズムが用いられている。つまりビッグデータの解析の難しさは、アルゴリズムにあるのではない。
もっとも難しい問題は「中くらいのデータ」や「小さなデータ」です。ここでベイズ主義が生きてくる。
ベイズの定理
ベイズの定理(ベイズ則)
P( A | X ) = \displaystyle \frac{ P(X | A) P(A) } {P(X) }
ベイズ推論は事前確率$P(A)$と更新後の事後確率$P(A|X)$を数学的に結び付けているだけである。
確率分布
離散値の場合
$Z$が離散値の場合は、確率分布は確率質量分布となる。これは$Z$は$k$をとる確率である。これを$P(Z=k)$と表す。
確率質量関数にポアソン分布がある。
$Z$の確率質量関数は、ポアソン分布に従い、次の式で表されます。
P(Z = k) =\frac{ \lambda^k e^{-\lambda} }{k!}, \; \; k=0,1,2, \dots
$\lambda$は、分布の形状を決めるパラメーターで、ポアソン分布の場合は$\lambda$は正の実数である。$\lambda$を大きくすると大きな値の確率が高くなり、$\lambda$を小さくすると小さな値の確率が高くなる。つまり$\lambda$はポアソン分布の強度である。
$k$は、非負の整数である。$k$は整数であるところに注意する。
確率変数$Z$がポアソン分布に従うことを次のように書く。
Z\sim \text{Poi}(\lambda)
ポアソン分布の便利な性質は、期待値が分布パラメーターに等しいところである。
E\large[ \;Z\; | \; \lambda \;\large] = \lambda
$\lambda$を変えて確率質量関数をプロットしたものである。
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import scipy.stats as stats
import numpy as np
a = np.arange(25)
# scipy のポアソン分布関数
poi = stats.poisson
lambda_ = [1.5, 4.25,8.50]
colours = ["#348ABD", "#A60628","#5AFF19"]
plt.bar(a, poi.pmf(a, lambda_[0]), color=colours[0],
label="$\lambda = %.1f$" % lambda_[0], alpha=0.60,
edgecolor=colours[0], lw="3")
plt.bar(a, poi.pmf(a, lambda_[1]), color=colours[1],
label="$\lambda = %.1f$" % lambda_[1], alpha=0.60,
edgecolor=colours[1], lw="3")
plt.bar(a, poi.pmf(a, lambda_[2]), color=colours[2],
label="$\lambda = %.1f$" % lambda_[2], alpha=0.60,
edgecolor=colours[1], lw="3")
plt.xticks(a + 0.4, a)
plt.legend()
plt.ylabel("probability of $k$")
plt.xlabel("$k$")
plt.title("Probability mass function of a Poisson random variable;\
differing \$\lambda$ values");
本は、$\lambda=1.5,4.25$の2つだったので、もう一つ8.5を入れて3つを計算してみた。
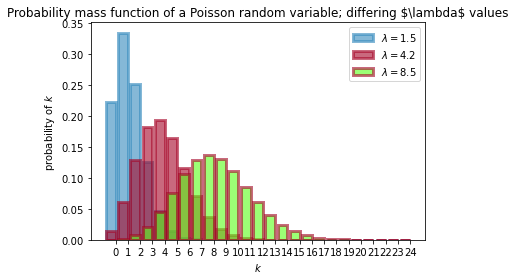
$\lambda$を大きくすると大きな値の確率が高くなり、$\lambda$を小さくすると小さな値の確率が高くなるが結果としてグラフに表れている。
連続値の場合
連続確率変数、確率質量変数ではなく、確率密度分布関数で表される。
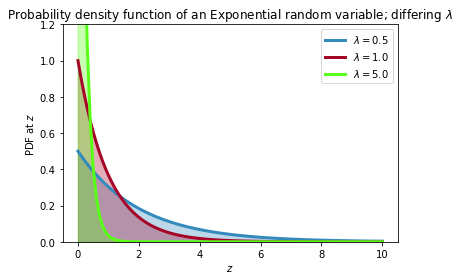
確率密度関数には指数分布がある。
f_Z(z | \lambda) = \lambda e^{-\lambda z }, \;\; z\ge 0
指数分布の確率変数は非負の値をとる。連続値であるので、時間や温度(ケルビン)などの正の実数値をとるデータに向いている。
確率変数$Z$は、密度分布関数が指数分布であれば、$Z$は指数分布に従います。つまり
Z \sim \text{Exp}(\lambda)
で表され、指数分布の期待値は、パラメータ$\lambda$の逆数になります。
E[\; Z \;|\; \lambda \;] = \frac{1}{\lambda}
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import scipy.stats as stats
import numpy as np
a = np.linspace(0, 10, 100)
expo = stats.expon
lambda_ = [0.5, 1, 5]
colours = ["#348ABD", "#A60628","#5AFF19"]
for l, c in zip(lambda_, colours):
plt.plot(a, expo.pdf(a, scale=1./l), lw=3,
color=c, label="$\lambda =!
%.1f$" % l)
plt.fill_between(a, expo.pdf(a, scale=1./l), color=c, alpha=.33)
plt.legend()
plt.ylabel("PDF at $z$")
plt.xlabel("$z$")
plt.ylim(0,1.2)
plt.title("Probability density function of an Exponential random variable;\
differing $\lambda$");
λとはなんだろう?
$\lambda$を得ることはできない。我々にわかるのは、$Z$のみである。また$\lambda$と$Z$にも1体1の関係がない。
ベイズ推論が扱うのは、$\lambda$の値が何なのか?の信念である。つまり重要なのは厳密に$\lambda$の値を求めるのではなく、$\lambda$はこの値になりそうだということにする、$\lambda$についての確率分布を考えることだ。
$\lambda$は定数だから確率変数ではないし、どうみたってランダムではない、確率変数でない定数の値にどうやって確率を与えられるということを思ったら、それはすでにあなたは頻度主義に侵されているということである。
ベイズ主義は、確率を信念だとみなすので、実は、何にでも確率を割り当てることができる。
つまり
「確率とは信念である」
ということである。