1.はじめに
先日、下記のqiita記事を投稿しました。
最も簡単な「一次のローパスフィルタ」を作る方法
この記事、1時間程度でさくっと書いたのですが想定外にいいね!が伸び、結果として私が書いた記事の中で最多いいねになりました。初歩的な内容であるにも関わらず、です。
この反響に対し私が気付いたのは、制御屋(しかもコテコテの古典制御屋)の私にとってはローパスフィルタは当たり前技術なのですが、qiita読者の当たり前ではなかったということです。
じゃあqiita読者の当たり前は何かというと、恐らくですが移動平均フィルタです。ちなみに私の移動平均フィルタに対する印象は下記になります。
n回平均フィルタ、カットオフ周波数がいくつか分からないから好きじゃない。カットオフが分からないと制御系の設計できないじゃん。
— モータ制御マン (@motorcontrolman) September 28, 2019
また上記私のツイートに付随して、下記の興味深いコメントを頂きました。
統計データの処理はダイナミクスの制約ないからしょうがないね
— ウータン (@usagi_utan) September 28, 2019
統計屋さんと制御屋さんは割と溝が深いと勝手に思ってる
このコメントを見て私は初めて、移動平均フィルタ=統計学的アプローチのフィルタと気づき、目から鱗が落ちるような感覚を味わいました。
また同時に、私の記事が伸びたのはその逆の現象が起きたせいではないか?と思いました。すなわち、統計学に興味を持つqiita読者からすると、ローパスフィルタ=制御工学的アプローチのフィルタの記事が目から鱗であったのでは、と。
単純なフィルタで、これほどの文化の違いがあるというのは非常に興味深いです。なので本記事では、2つの分野におけるフィルタの考え方の差異や、使い分けの方法について考察するものとします。
なお私は統計学については門外漢になります。なので統計学の部分の内容について誤りがあれば、積極的に指摘頂けるとありがたいです。
2.統計学におけるフィルタの考え方
フィルタの考え方を示す前に、まずフィルタで対処したいノイズの考え方を示す必要があります。統計学におけるノイズは、例えばガウスノイズのような分布に関するノイズです。
本章ではデータ真値は時間ごとに変化するものとし、実際のデータは分布ノイズを含む場合を考えます。この前提は超大事です。
具体例として温度yが1分で1℃上昇するものとし、データは0.1秒ごと取得可能とします。ノイズはσ=0.1のガウスノイズであるとします。下図において青線が真値、赤丸が実データです。
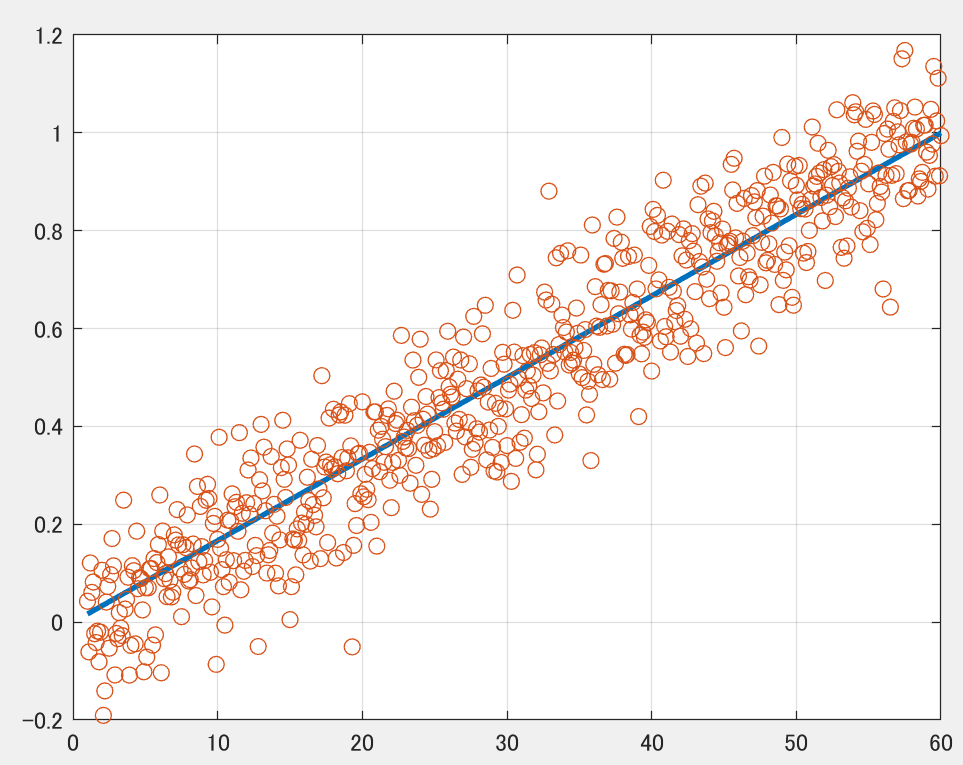
t = [1:0.1:60];
y = t/60; %真値
n = 0.1*randn(size(t)); %σ=0.1のガウスノイズ
yv = y+n; %実データ=真値+ノイズ
plot(t,y,'LineWidth',2);hold on;grid on;
scatter(t,yv);grid on;
ノイズの分布をヒストリグラムで見ると、当然ながら正規分布となっていることが分かります。
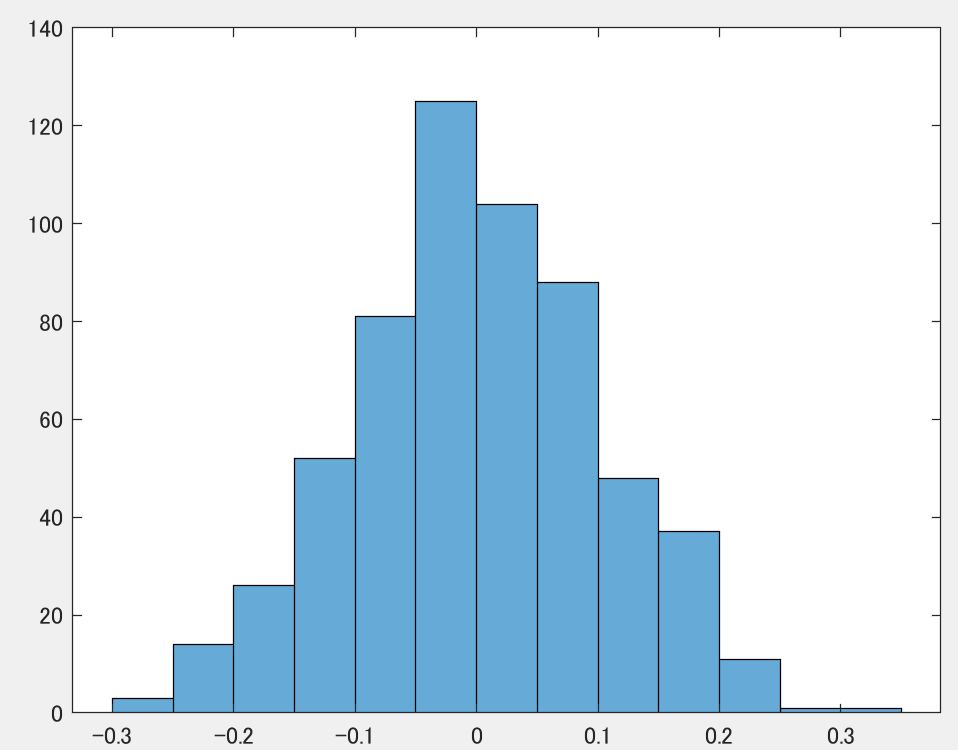
次にフィルタリングです。ここではまずノイズだけに関して考えるものとします。
移動平均フィルタにおいて平均を取るデータの数(以降ではサンプル数と呼ぶものとします)を増加することでσを下げられます。下記は赤がサンプル数=5回、黄色が10回の場合。
n_FIL = zeros(size(n));
samp = 5;
for i = samp:length(n)
n_FIL(i) = mean(n(i+1-samp:i));
end
figure(1);
histogram(n);hold on;
histogram(n_FIL(samp:end));
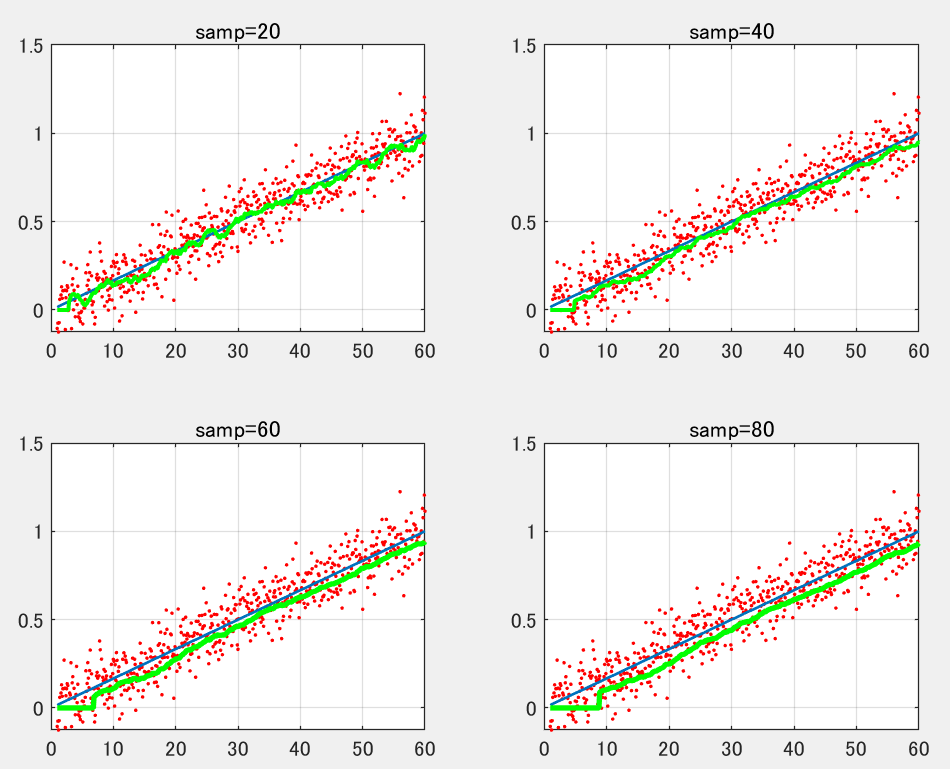
上記はノイズだけに関しての議論でした。真値とノイズが合わさった実データに対し移動平均フィルタを適用すると下記のようになります。下記サンプル数sampを20から80まで変化させた場合を示します。
yv_FIL = zeros(size(n));
samp = 20;
for i = samp:length(n)
yv_FIL(i) = mean(yv(i+1-samp:i));
end
サンプル数を増すほどノイズ起因の誤差が抑えられる一方、フィルタリング起因の誤差が増大するトレードオフ関係が見て取れます。ここで誤差(真値-実データ)の標準偏差・平均値とデータ数の関係を示してみます。赤が標準偏差、青が平均値です。横軸はデータ数。
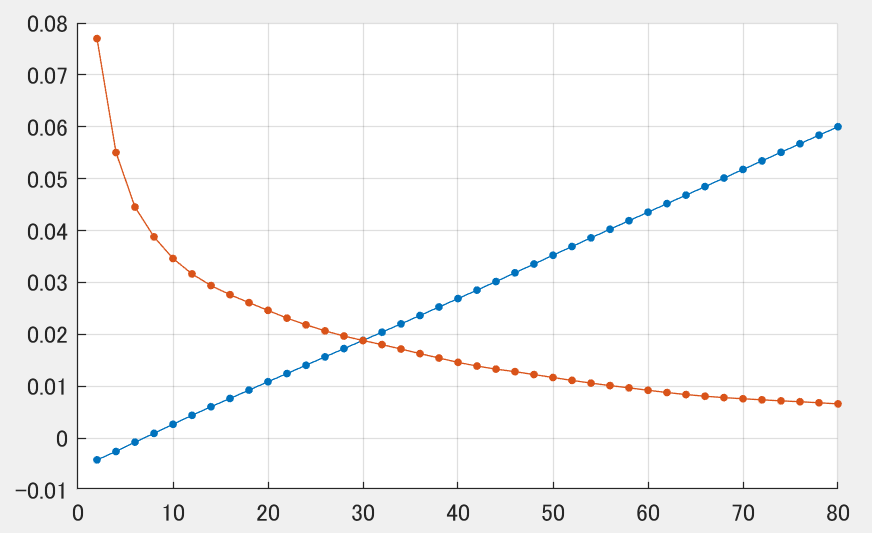
統計学の視点においては、フィルタ設計はこの標準偏差と平均値的誤差のトレードオフ関係(あるいはノイズ起因誤差とフィルタ起因誤差のトレードオフ)を基準に行われているのではないでしょうか。このトレードオフはデータ真値が時間変化することに伴って発生するもので、どこにでも発生しうる問題であると言えます。
なおオフライン処理を前提とするなら、フィルタ結果を時間シフトすることで上記問題は割と容易に解決できるはずです。オンラインの場合はかなりやっかいですね。
3.制御工学(古典制御)におけるフィルタの考え方
制御工学におけるノイズは、周波数に関するノイズです。周波数に関するノイズで一番分かり易いのは機械的なもので、ガタガタ・ブルブルといった望ましくない振動をノイズとして捉えます。同様のノイズは電気的にも存在するため、例えば温度をセンサにて測定する場合なんかは測定対象そのものにノイズが無くても、センサの電気的特性を原因とした周波数ノイズが発生しえます。ただし各種メーカがそうならないよう努力しているので、普通は発生しませんが…(センサを自作する場合なんかは要注意)
本章において、データ真値は統計学の場合と同様に時間ごと変化すると仮定する一方、実際のデータは周波数に関するノイズを含む場合を考えます。
具体例として温度yが1分で1℃上昇するものとし、データは0.1秒ごと(すなわち10Hzで)取得可能とします。ノイズは0.5Hz,1Hz,3Hzのノイズが合わさったものとします。下記青線が真値、赤丸が実データです。
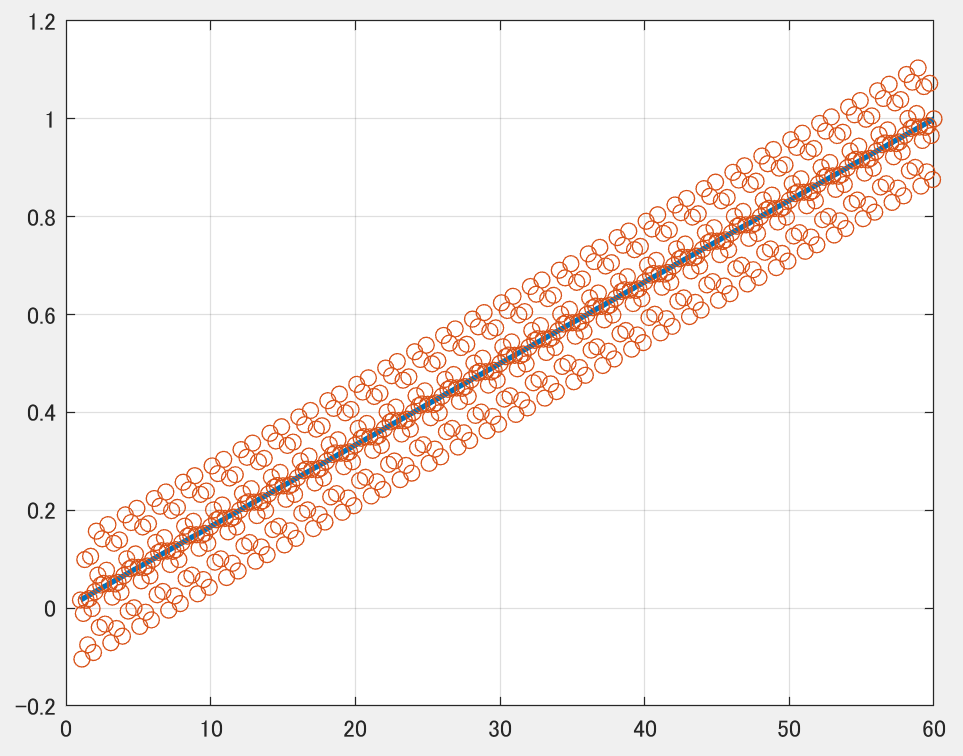
%0.5Hz,1Hz,3Hzのノイズ 振幅は適当
nw = 0.02*sin(0.5*2*pi*t)+ 0.02*sin(1*2*pi*t) + 0.1*sin(3*2*pi*t);
yw = y + nw;
plot(t,y,'LineWidth',2);hold on;grid on;
scatter(t,yw);grid on;
ガウスノイズと比べると何かしらの周期性は見て取れます。ただ実際は、分布ノイズと周波数ノイズの両方が(程度問題こそあれ)同時に発生するので、上記ほど綺麗な波形にはならない場合が多いです。
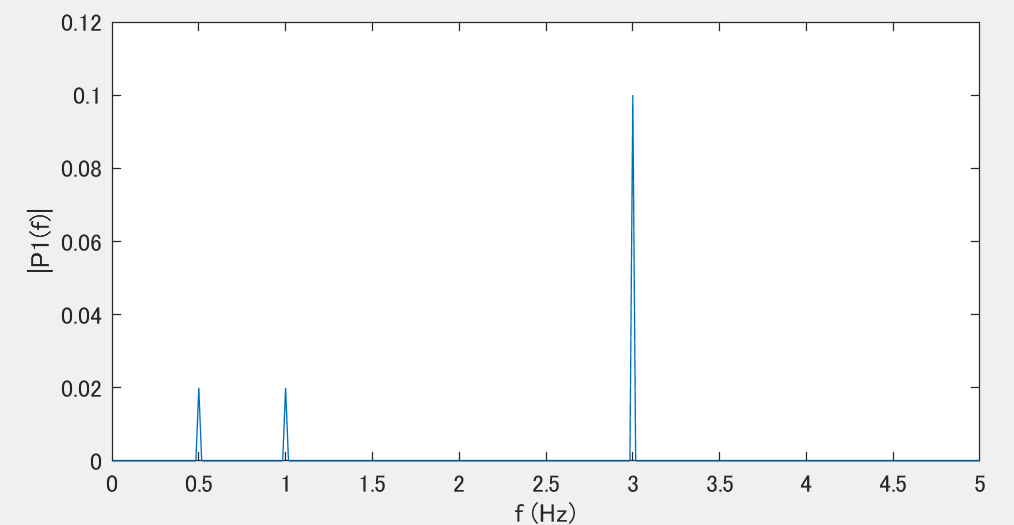
周波数ノイズの分布を見るための道具がフーリエ変換で、結果は下記です。当然ながら与えた通りの周波数で与えた通りの強さを示すスペクトルが得られます。
Y = fft(nw);
L = length(nw);
P2 = abs(Y/L);P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
f = F*(0:(L/2))/L;
plot(f,P1)
んじゃヒストグラムは?と思って見てみると、なんか正規分布っぽく見えてしまいます。ただこれはあくまでたまたまです。周波数ノイズも場合によっては分布ノイズに見える場合があります。ただ周波数ノイズを分布ノイズと勘違いして処理すると後で痛い目を見ます、多分。
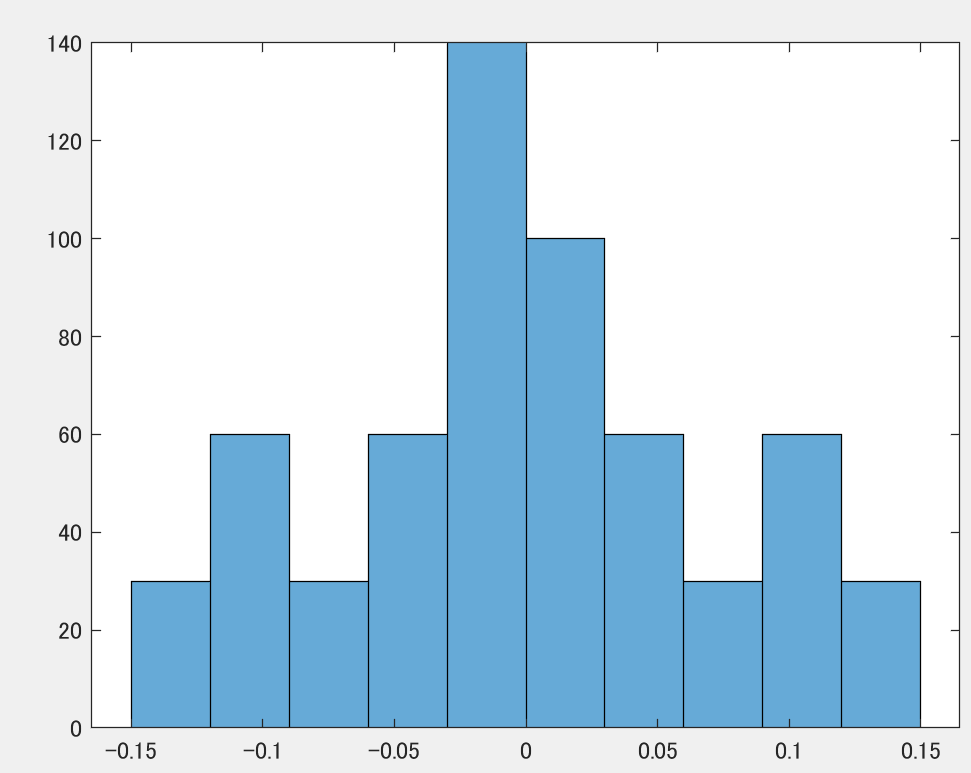
次にフィルタリングです。ここではまずノイズだけに関して考えるものとします。
制御工学的フィルタであるローパスフィルタの設計パラメータはカットオフ周波数Fcであり、Fc以上の周波数ノイズを抑制する効果があります。
ちなみにカットオフ周波数Fcのローパスフィルタは、周波数Fcのノイズを30%カットする効果があります。これはローパスフィルタの伝達方程式から求められます。
G(s)=\frac{1}{1+\tau s}\\
\tau = \frac{1}{2\pi F_c} \,より\\
G(s)=\frac{2\pi F_c}{2\pi F_c+ s}\\
s=j2\pi F_c \,のとき\\
G(j2\pi F_c)=\frac{2\pi F_c}{2\pi F_c+ j2\pi F_c}=\frac{1}{1+j}\\
|G(j2\pi F_c)|=\frac{1}{\sqrt{ 2}} \approx 0.7
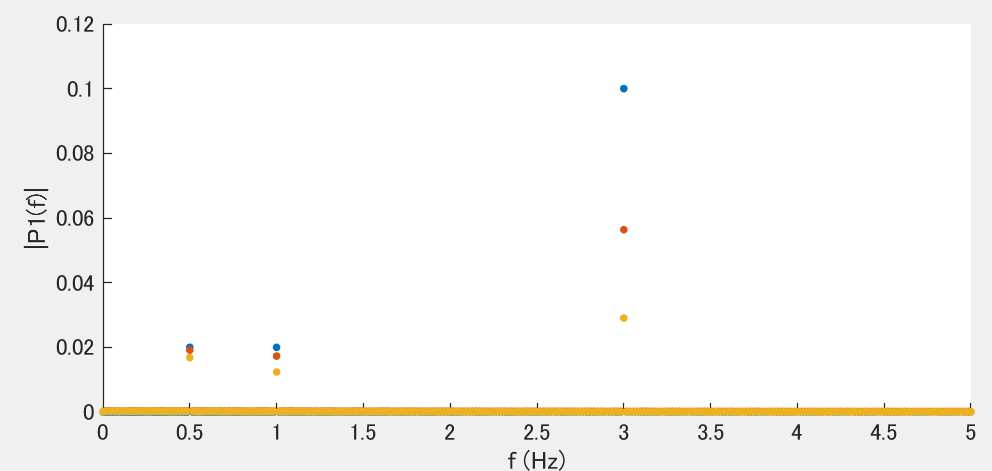
下記Fc=3Hzの結果を赤で、Fc=1Hzの結果を黄色で示します。線だと見にくかったので点で示しています。
概ね想定通りの結果が得られています。3Hzの赤点が0.07にならないのは離散化誤差の影響で、サンプル周期10Hzに対し3Hzのローパスという苦しい設定に起因しています。仕方ないね。
上記はノイズだけに関しての議論でした。以下では真値とノイズが合わさった実データに対しローパスフィルタを適用します。下記カットオフ周波数Fcを1Hzから0.033Hzまで(対数的に等間隔に)変化させた場合を示します。
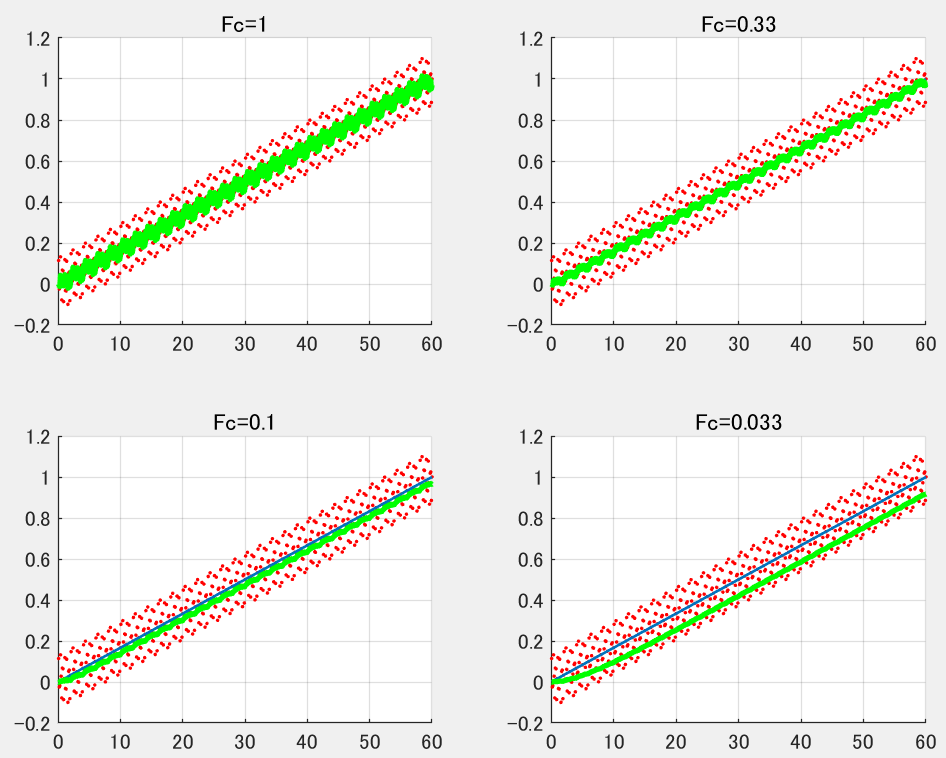
移動平均フィルタの場合と同様、Fcを減少させるほどノイズ起因の誤差が抑えられる一方、フィルタリング起因の誤差が増大するトレードオフ関係が見て取れます。
ただし、制御屋視点からするとこのトレードオフ関係はさして重要ではありません。重要なのは、制御システムの即応性と精度(または安定性)のトレードオフ関係です。上記得られたデータはあくまで制御システムを構成する一部分に過ぎないのです。
上記は温度を想定しているので、制御システムの具体例としてエアコンの温度制御を考えます。
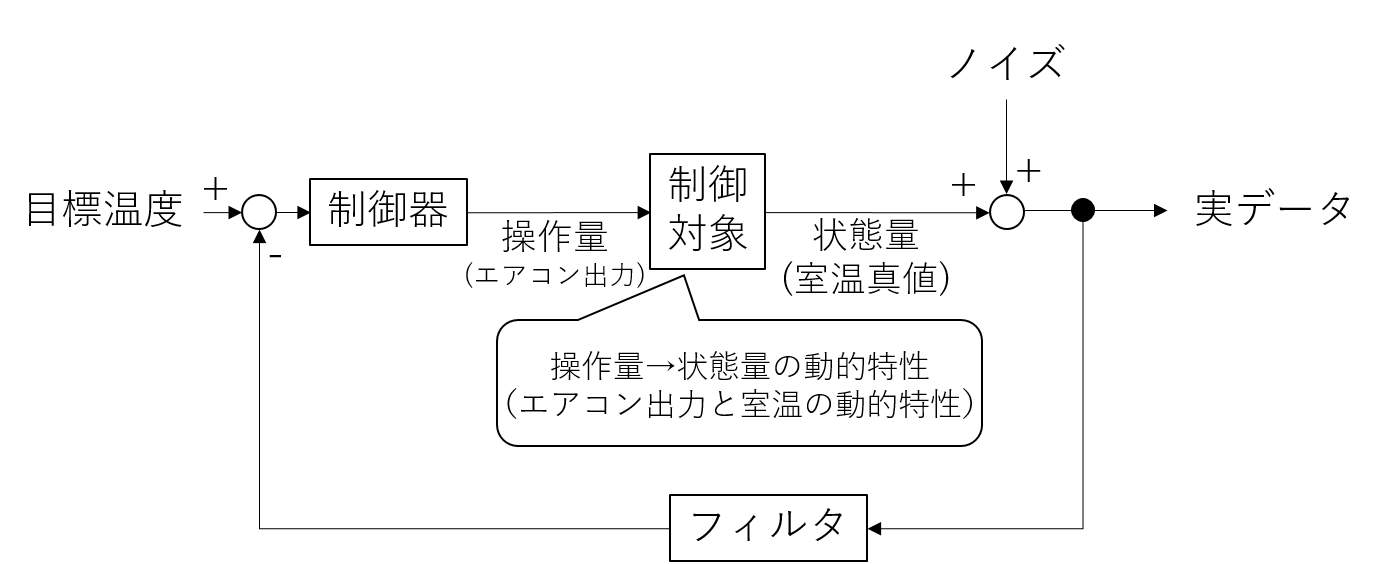
制御屋にとってのミッションは、室温を高速かつ高精度・高安定に目標温度に制御することです。このため設計の対象は制御器とフィルタの両方であるため、フィルタ単体のトレードオフ関係はそれほど重要ではなく、システム全体のトレードオフが重要になるのです。
では何を基準としてフィルタを設計するかというと、ノイズの周波数特性に基づいてまず決めるのが基本です。すなわち、フーリエ変換の結果が分かればフィルタの設計はほとんど決まってしまうのです。
そんなんでいいのかと思われるかも知れませんが、これには前提があります。それはシステムにおける即応性の目標(システムの目標応答周波数と言う)と、フィルタのカットオフ周波数が十分に離れていることです。システムに対しフィルタの周波数が概ね5倍以上離れてる場合、フィルタはそのままであとは制御器を目標通りになるよう設計すれば制御屋の仕事は終わりです。
十分に離れていない場合、この場合こそが制御屋としての出番です。2帯域がちょっと近いな、という場合はフィルタのカットオフ周波数を上げてみます。そうすると、ノイズを完全に消去できないため制御の精度は下がります。精度を重視する場合はシステムの目標応答周波数を下げることでシステムは成立しますが、要求性能未満にしてはいけません。このトレードオフ関係のもとでシステム要求を成立させることこそが制御屋にとっての仕事であり、醍醐味でもあります。
なお、余りにも2帯域が近い場合やシステム周波数>フィルタ周波数の場合、システムを成立させるのは無理ゲーなのでシステム要求性能を妥協して頂くか、もっとまともなセンサがないのかを検討する必要があります。こういのも広い意味では制御屋の仕事の1つと思います。
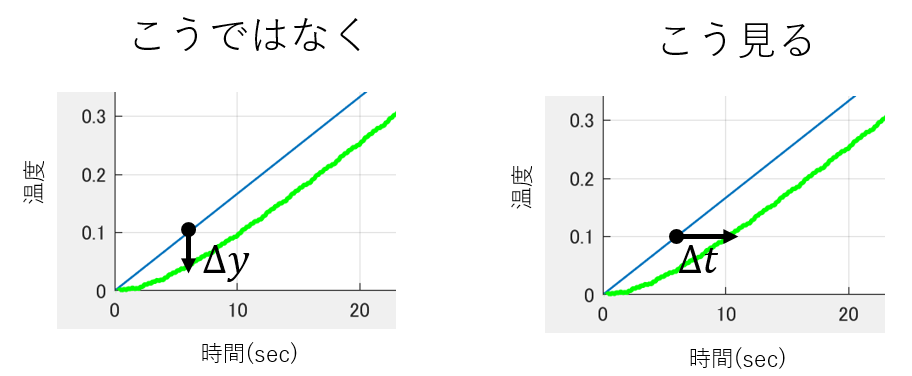
ちなみにですが、ローパスフィルタのカットオフ周波数が低いことはフィルタ出力が入力に対し遅延が大きいことと言い換えられます。遅延は制御システム設計にとって大敵なので、多分ですが制御屋がフィルタ入出力差異を見るときは時間軸で見たりします。統計学はその対象によってマチマチと思いますが、制御屋ほど遅延を目の敵にはしていないと思われます。
4.どっちのフィルタが正解か
私見ですが、「そんなん、ノイズの種類によって変わるわ」が私の考えです。すなわち、ノイズの主成分が分布ノイズであるなら統計学的=移動平均フィルタを使えばいいし、周波数ノイズであるなら制御工学的=ローパスフィルタを使えばよいのです。
遅延が問題にならない状況下であるなら、周波数ノイズに対し移動平均フィルタを使っても表面上は問題はありません。が、これはあくまでも現状のシステムがそうだからというだけで、要求性能が変われば問題となりえます。なので周波数ノイズとあらかじめ分かっているならローパスフィルタを選択して下さい、お願いします。(移動平均フィルタのレガシーコードに制御屋が悩まされるという事例があったりするので…)
また逆に、分布ノイズに対してローパスフィルタを使うのは不適切というケースも当然あります。統計学の視点からするとローパスフィルタは「重み付き移動平均フィルタ、重みは現在ほど大きく過去ほど小さい」なので意図せずして時間の概念が入り込みます。時間の概念を統計結果に織り込んでもよいかどうか、考えた上で適用する必要があります。
設計者が意図して使う限りでは、移動平均とローパスを併用したり、これらを直列結合させるのもありだと思います。なぜなら実際には分布ノイズと周波数ノイズは同時に起こるものなので。この切り分けは非常に難しいですが、ノイズの発生原因が何であるかを明らかにするしかありません。専門が統計学であっても制御工学であっても、適切なフィルタ設計にはシステム全体に目をやることが重要なことと思います。
冒頭のツイートにもあったように、統計学の専門家と制御屋との溝は案外深く、これは文化的な違いによるものと思います。お互いが歩み寄れればもっとよい製品、もっとよいサービスの実現に繋がると思いますので、この記事が相互理解の助けになれば幸いです(今更)
5.おまけ カルマンフィルタは制御・統計どっち寄り?
カルマンフィルタは制御工学に由来を持ちますが、対象とするノイズはガウスノイズ=分布ノイズ=統計学におけるノイズであるためちょっと扱いが難しいと思います。
古典制御に軸足を置く私からすれば、カルマンフィルタは「統計学と制御工学のいいとこ取り」と考えるとしっくりきます。これ、現代制御に軸足を置く人が聞いたら怒るかも知れません、笑。
明確に制御工学に分類される技術としてシミュレータとオブザーバがあります。
オブザーバによる状態推定
シミュレータは制御対象のモデルと制御対象の入力信号を使うことで制御対象の出力を推定する方法で、上記リンクにおいて、オブザーバゲイン=0の場合がシミュレータと言えます。シミュレータでは一度発生した推定誤差は消えずに残り続け、このため推定が正しくできない問題があります。
オブザーバは上記問題を解決したもので、推定した出力のうちで可観測なものについて推定値と観測値の誤差を計測、誤差をもとに推定値の修正を行うものです。
オブザーバが面白いのは、この推定値の修正機構によって不可観測出力の推定が高信頼化されることで、これはすなわち本来観測できない値を推定できることを意味します。オブザーバはノイズ対策のための技術ではなく、未知数推定のための技術であるためフィルタとは言えません。
シミュレータおよびオブザーバで大事なのはモデルを用いているという点です。モデル、特に動的な振る舞いを記述したモデル(伝達関数または状態方程式)の利用は制御工学における最大の発明の一つと言えます。
一方でカルマンフィルタはというと、形はオブザーバとほぼ同じですが出来ることが違います。
カルマンフィルタとは ←オブザーバのリンクと見比べて下さい。
カルマンフィルタで可能なことの1つに、本来観測できない値を推定するのではなく、観測値に含まれる分布ノイズの除去が挙げられます。この点においてはカルマンフィルタはオブザーバの延長ではなく、いずれもシミュレータの派生技術であって親戚のような関係と言えます。
(なお、カルマンフィルタで「観測できない値の推定」を行うことも可能です。本稿では話の単純化のため、カルマンフィルタ=「観測値ノイズの除去器」として以降の議論を行います。)
カルマンフィルタのうち、シミュレータの部分(すなわちモデルの利用)は間違いなく制御工学由来です。これに対し、カルマンゲインの計算は統計学由来です。このため、著者としてはカルマンフィルタは「統計学と制御工学のいいとこ取り」と考えます。
6.おまけ2 カルマンフィルタの使いどころ
カルマンフィルタは分布ノイズへの対策としては非常に強力です。特に2章で述べたような、リアルタイム性の求められるシーンでは猛威を発揮します。なぜって、カルマンフィルタはその特性上、遅れが発生しないからです。←認識違いがあったので削除します。
ただしカルマンフィルタには確からしいモデルが必要とされるので、モデルが不明確な状態で使うことは推奨されません。移動平均フィルタはその点、モデルフリーなのでモデルが不確かであればこれはこれで有効な手段と言えます。
カルマンフィルタの出力は、分布ノイズ起因の数値誤差とモデル誤差起因の数値誤差が合わさる形になるので、かえって考察を難しくする弊害があります。なので、なんでもかんでもカルマンフィルタ使えばいいということはありません。その点、移動平均フィルタは話をややこしくしない点が優れます。
一方、周波数ノイズに対しては、カルマンフィルタを使うのは、遅れが発生しない観点からするとよさそうですがそうでもありません。なぜなら、カルマンゲインの計算はガウス分布を前提とするので周波数ノイズに対し適用するとおかしなことになります。じゃあ他に対策はないのかというと、個人的な見解ですがオブザーバの併用が有効です。
実データとオブザーバの偏差からノイズだけを取り出しフーリエ級数展開、ノイズを相殺する信号を生成して実データからしょっぴく、という周波数ノイズ対策は単純ながらかなり強力です。
ただしこれも、確からしいモデルが必要になるのでなんでもかんでもこれ使えばいいという事ではありません。移動平均フィルタ同様、ローパスフィルタもモデルフリーである点が優れます。
「どのフィルタを使うべきか」はエンジニアの腕の見せ所と思います。移動平均フィルタやローパスフィルタを冷遇することなく、場面に合わせて使い分けられるこなせる事こそがチョットデキルエンジニアとしての理想ではないでしょうか。