はじめに
MATLABのツールボックスの1つにGlobal Optimization Toolbox(以下GOTと表記)があります。
Optimization Toolbox(OTと表記)と名前は似てますが別のツールボックスです。「Global」は何なのかというと、**大域的最適解(Global minimum/maximum)**のGlobalです。
大域的最適解については下記のページが参考になります。
最適化アルゴリズムを評価するベンチマーク関数まとめ
OTに準備された解法は基本的に、局所最適解にしか対応していません。局所最適解と大域的最適解が一致しているのであればこれで問題ありませんが、不一致の場合はGOTを用いる必要があります。
こう書くと「んじゃとりあえずGOT使っとけばいいんじゃね?」と思われるかも知れませんがそうはなりません。なぜかというと、Globalな解法は大域的最適解の存在を前提とすることで計算量が増し増しになりますので(要出展)。また、そもそも論としてGlobalな解法とそうでない解法は大幅にアプローチが違うので、問題によって使い分ける必要があります。
さておき、最適化と言ったらまずはGlobalじゃない方法を使うのが一般的と思います。MATLABのツールボックスも同様で、広く用いられているのはOTのほうだと思われます。
このためかGlobal Optimization Toolboxは日本語ドキュメントがなく、とっつきにくい状況でした。が、@k_hashiko さんが日本語の解説記事書いてくれました。ありがてぇありがてぇ。
MATLABのGlobal Optimization Toolboxの使い方(GA実践編)
そうなるとGOTおよびGA=遺伝的アルゴリズムで遊びたくなるのがMATLAB芸人のサガです。
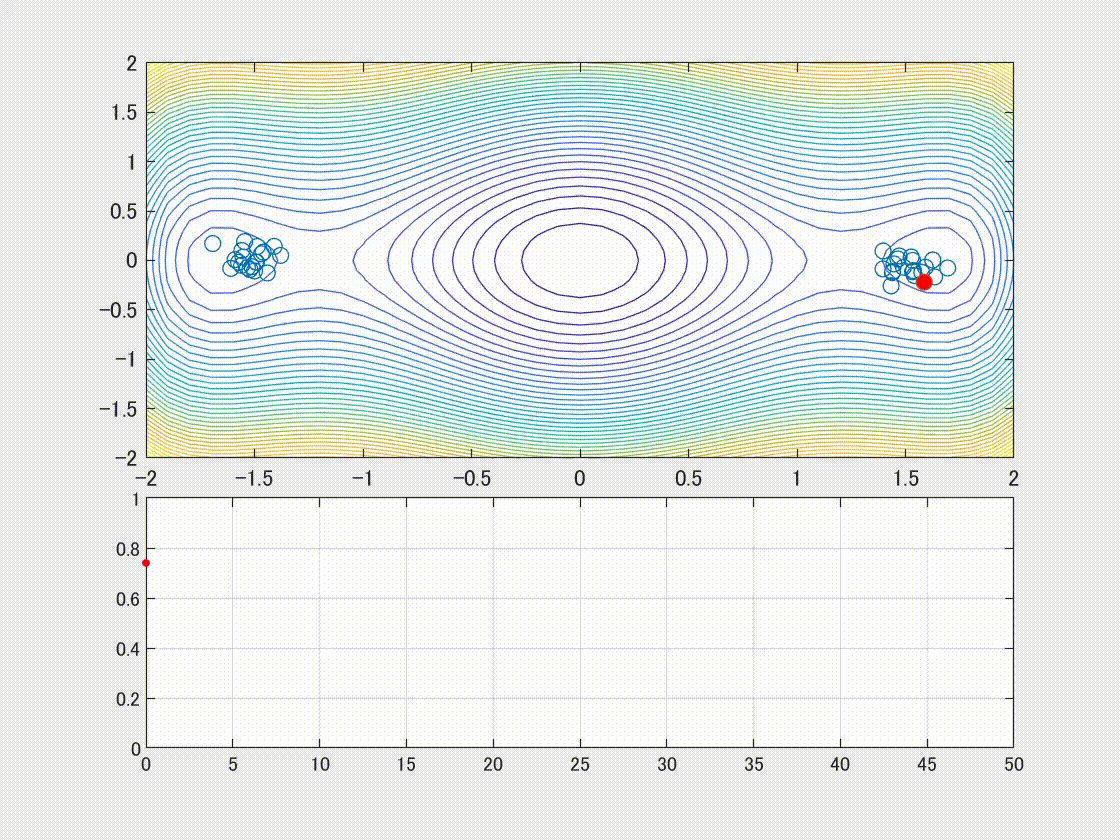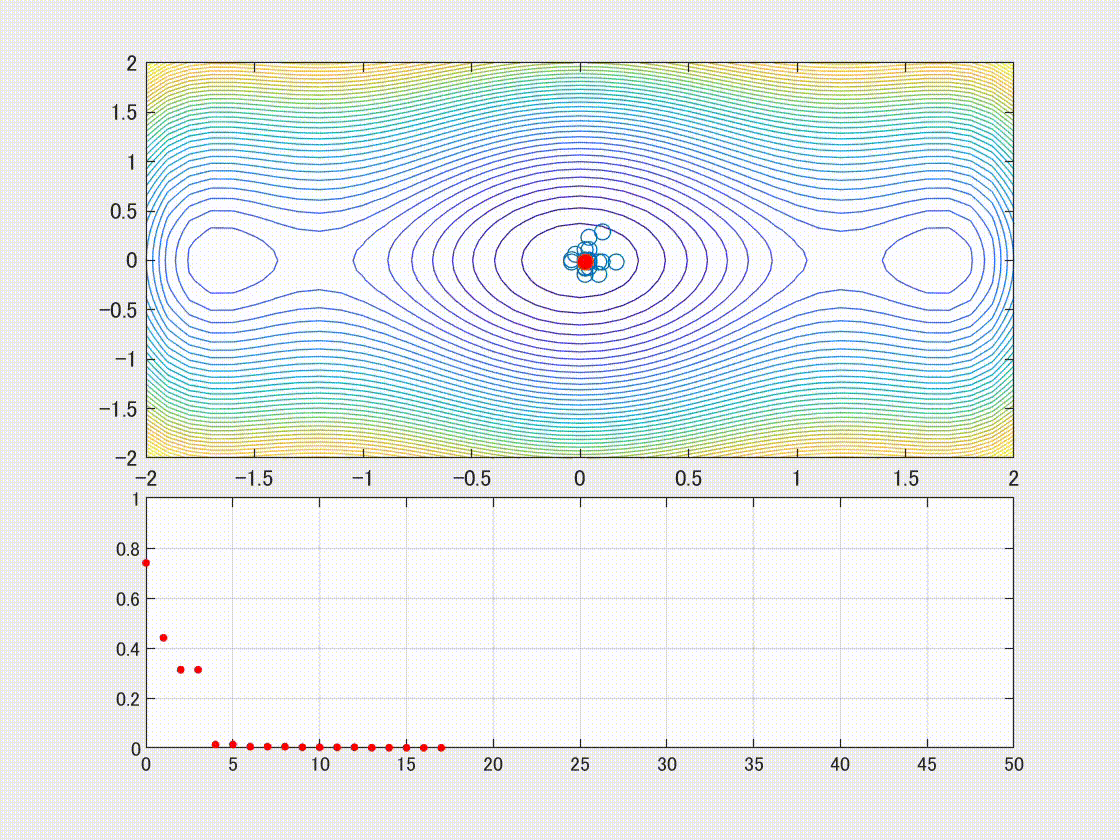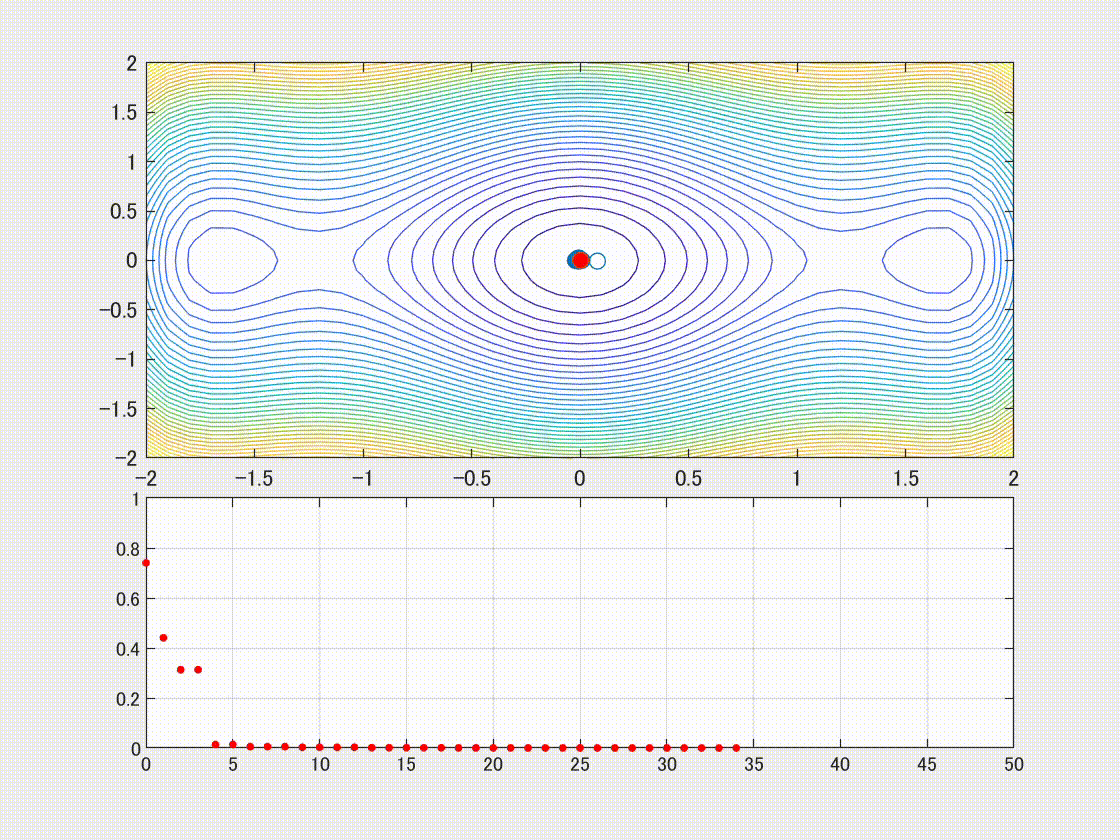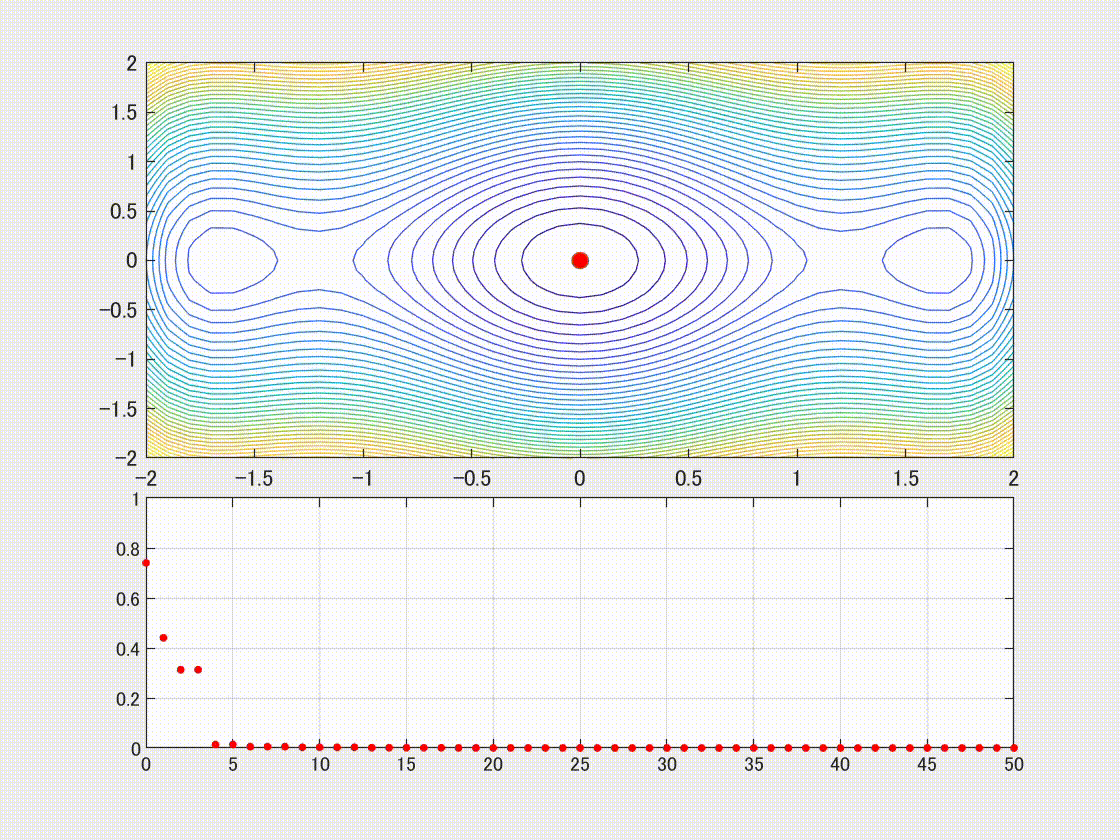
遺伝的アルゴリズムのイケてるポイントといえばやはり「集団」「世代」です。これを可視化せずにおられるか! ということで、頑張って可視化しました。今回はそのレシピを公開、説明を加えていきます。
アドベントカレンダーを参考にして早速遺伝的アルゴリズムで遊んでいる、@wsq_stew さんに感謝。解(0,0)から遠くに初期集団を置いてもちゃんと辿り着く、すごい。
— モータ制御マン (@motorcontrolman) December 15, 2019
そして2年ほど前の妄想「万能だけども利用にコツが要るMATLABをみんなで解説しあうことでみんな最強になる」が実現してるのを感じる。 pic.twitter.com/ExctRzvn6r
ちなみにGAの可視化はそれなりに面倒なので、普通に使う分にはやらないに越したことはないです。でもでも、やっぱり可視化したくなっちゃうんだな~、これが。
以下ではMATLABのバージョンは2019bを利用,ツールボックスはGlobal Optimization Toolbox と Optimization Toolboxが必要です。コードが欲しい方は下記にてどうぞ。
https://github.com/motorcontrolman/Ga_Visualize
1.動画作成のためのおまじない
最適化の途中経過を可視化&動画化する と同じ処理ではありますが振り返りも含めて。vidObjをグローバル宣言することで出力関数内で動画作成できるようよう準備しておきます。
clear all;
close all;
global vidObj;
vidObj = VideoWriter('result.mp4','MPEG-4');
vidObj.FrameRate = 1/0.2;
open(vidObj); %動画の書き込み開始
2.画面レイアウトを設定、背景までを描画
今回はちょっとレイアウトにも凝ってみましょう。遺伝的アルゴリズムの「集団」「世代」という考え方が際立つような画面レイアウトにしたいですね。
「世代」は通常の最適化のiterationみたいなものなので画面に占める面積は控えめにして、「集団」の面積を広めに取りましょう。@eigs さんのこのプロットどうやって描いたの? を参考に、「集団」と「世代」の画面レイアウトを3:2にします。
また「集団」が大域的最適解に対してどう動いたかを可視化したいので、「集団」の画面の背景として等高線を描画します。
f = figure; % figureのハンドルを作成
subplot(5,1,[1:3]); % 「集団」用の画面を確保
x = [-2:0.1:2]; % 等高線作成用のx軸データ
y = x; % 同じくy軸データ 今回はx軸と同値とする
[xx, yy]=meshgrid(x,y); % 2次元グリッドの作成
Levels = 40; % 等高線の数
最適化の目的関数は多峰性のある three-hump-camel関数 とします。関数は別ファイルThreeHump.mとして保存してあります。
z = ThreeHump(xx,yy); % x,yを入力とした出力値をzに格納
% ThreeHump.mの中身は下記。
% function fval=ThreeHump(x1,x2)
% fval = 2 * x1.^2 - 1.05 * x1.^4 + x1.^6/6 + x1*x2 + x2.^2;
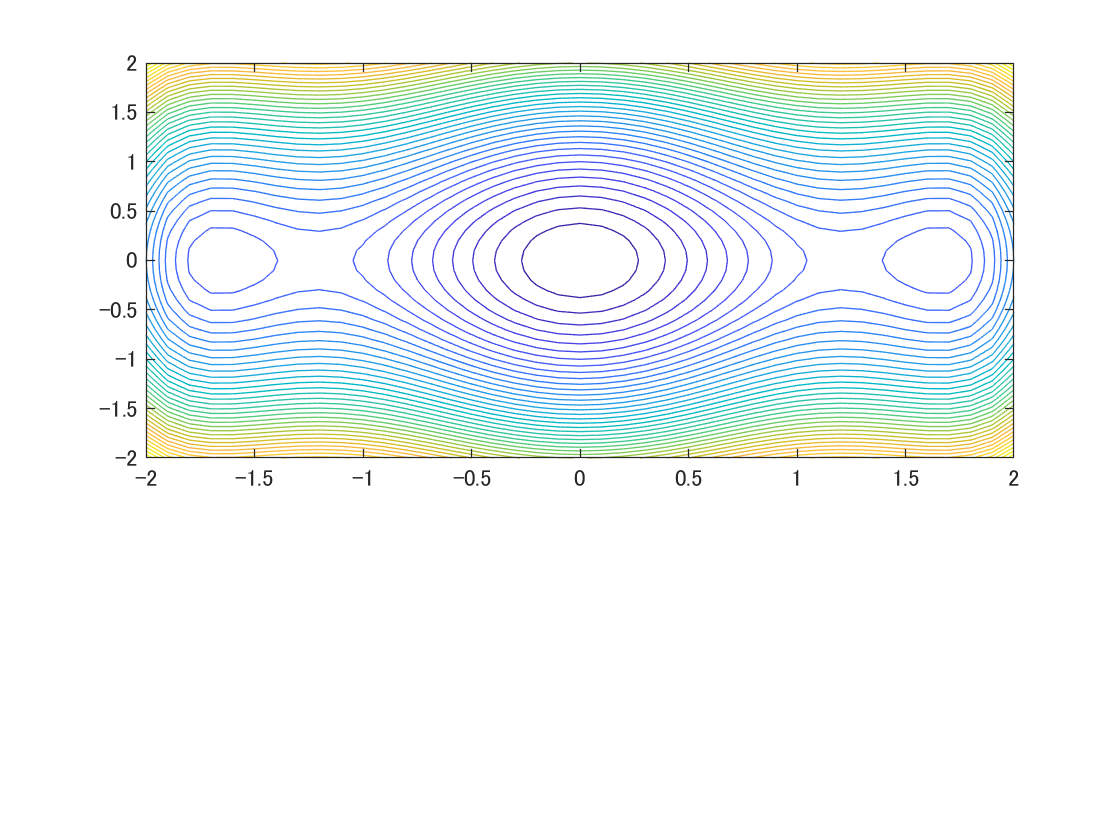
contour(x,y,z,Levels);hold on; % 等高線を描画
下記が動画の背景になります。なお大域的最適解は [0,0] 点にあります。
局所最適解は[-1.5,0] と[1.5,0]にあることが確認できます。
3.最適化関数に突っ込むため目的関数を変形
GAも他の最適化関数と同様、目的関数の引数は1つのベクトルしか許容しません。ThreeHump.mは2入力の関数として作成したので、1ベクトル入力の関数として再定義します。
fun=@(x) ThreeHump(x(1),x(2));
4.GAの初期集団を設定
Globalな解法であるGA特有の挙動を確認するために、初期集団を2つの局所的最適解 [1.5, 0] および[-1.5, 0]近傍からスタートさせます。
StartPoint1 = [1.5, 0]; % 初期集団その1の中心点
StartPoint2 = [-1.5, 0]; % 初期集団その2の中心点
% 分散0.1で正規分布する初期集団を2つ(人口20ずつ)を作成
initpop1 = 0.1*randn(20,2) + StartPoint1;
initpop2 = 0.1*randn(20,2) + StartPoint2;
% 2つの初期集団を結合、人口40
initpop = [initpop1;initpop2];
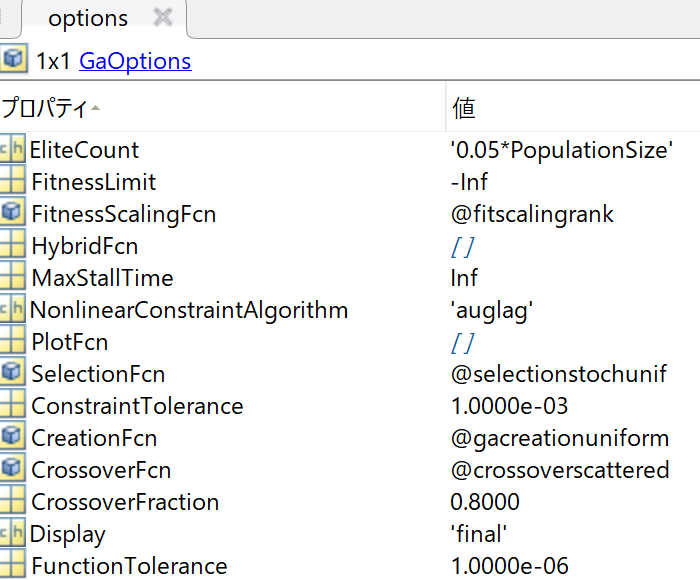
5.GA用の最適化オプションを設定
まずは最適化オプションを作成、その後で設定をしていく流れにします。もちろん作成時に設定を入れ込んでしまっても構いません。出力関数であるmyfunについては次章にて解説を行います。
options = optimoptions('ga','OutputFcn',@myfun);
設定はめっちゃいっぱいありますが、デフォルト値が設定されているのでこのまま最適化を実行することも出来ます。
今回は初期集団を決め打ちしたいので、それに関わる部分の設定を行います。また最適化にかける時間を抑えたいので、世代の最大値を控えめな値に設定します。
options.InitialPopulationMatrix = initpop; % 初期集団を設定
options.PopulationSize = length(initpop); % 人口数、初期集団以上を推奨。今回は初期集団と一致させる
options.MaxGenerations = 50; % 世代の最大値
上下限値の設定をした上で、最適化を走らせます。最適化の最中には出力関数myfunが毎度実行されます。
nvars = 2; % 最適化変数の数
lb = [-2; -2]; % x,yの下限
ub = [2; 2]; % x,yの上限
[x,fval]=ga(fun,nvars,[],[],[],[],lb,ub,[],options);
close(vidObj); % 動画の書き込み終了
6.出力関数myfunの内容解説
出力関数myfunはメインの関数とは別のファイルmyfun.mに記述してあります。実のところ、今回の動画化においてもっとも重要な部分はここだったりします。 面倒なので紙面の都合上、細かい解説は省きますが試される方はまずコピペしてみて、その上でデバッグ中に色々なプロパティを触ってみるとよいと思います。
function [state,options,optchanged] = myfun(options,state,flag)
%% 変数の設定
% 動画用オブジェクトをグローバル宣言
global vidObj;
% 永続変数の定義
persistent BestScoreHistry; % ベストスコアの履歴を格納
persistent ScatterHandle; % scatterコマンドのハンドル
persistent ScatterHandleBest; % scatterコマンドのハンドル、ベストスコア用
%% 世代におけるベストスコアの取得、およびインデックスの取得
BestScore = min(state.Score);
BestScoreIndex = find(state.Score == BestScore);
optchanged = false;
%% ベストスコア履歴の格納、およびfigureの上半分に「集団」をプロット
subplot(5,1,[1:3]);
switch flag
case 'init' % 探索初回における処理内容
BestScoreHistry(1) = BestScore;
ScatterHandle = scatter(state.Population(:,1),state.Population(:,2));
% ベストスコアだけ赤丸でプロット
ScatterHandleBest = scatter(state.Population(BestScoreIndex,1),state.Population(BestScoreIndex,2),'MarkerFaceColor','r');
case 'iter' % 探索初回以降における処理内容
BestScoreHistry = [BestScoreHistry, BestScore];
% ハンドルを使って各プロットのx,yを更新
ScatterHandle.XData = state.Population(:,1);
ScatterHandle.YData = state.Population(:,2);
ScatterHandleBest.XData = state.Population(BestScoreIndex,1);
ScatterHandleBest.YData = state.Population(BestScoreIndex,2);
drawnow
case 'done' % 探索完了時における処理内容
% ベストスコア履歴をベースワークスペースに渡す。省略可能
assignin('base','BestScoreHistry',BestScoreHistry)
end
%% figureの下半分に「世代」のベストスコアをプロット
subplot(5,1,[4:5]);
plot(state.Generation,BestScore,'.r','MarkerSize',10);hold on; grid on;
axis([0 50 0 1]);
おわりに
最適化計算の途中経過、本来やらなくてもいい事なのですがこうして可視化すると「どんなアルゴリズムなのか」がものすごく納得できてよいと思います。
そういうのが簡単に試せるのがMATLABのいいところなので、気になるアルゴリムがあれば可視化に挑戦してみてはいかがでしょうか。