はじめに
近年、教育系Youtuberを筆頭として「勉強」を楽しく学べる動画がYoutubeに数多く投稿されている。著者の専門分野である制御工学についても良質な動画が(他分野と比べると控えめではあるが)投稿されており、嬉しい限りである。
著者のお気に入りの動画を挙げ始めるとキリがないが、本記事では下記1つを挙げる。
上記の動画は、一見するとおふざけが過ぎるコミカルなだけのものであるが、制御初学者にとって躓きがちなボード線図を体操として捉え、全身を動かすことによって表現することで文字通り「体得」可能とした非常に素敵な動画であると著者は考えている。
あまりに素敵すぎて、実際に自分の体を使ってボード線図が書けたらいいなぁってつい思っちゃいますよね。私hは正直なところ2年ぐらい前からそう思っていました。しかしながら、当時はMATLABに姿勢推定のモデルがうまくインポートできずに挫折…という悲しい過去があります。
本記事は2年越しのMATLAB芸を、最新のMATLABを用いることで(割と)容易に実現できたことを祝して記載した内容になります。
なお、使用したMATLABのバージョンとしては2021aとなります。
また本MATLAB芸につきましては、年末年始に相応しく下記豪華絢爛なツールボックス群を用いておりますのでその点ご注意下さい。
・Computer Vision Toolbox
・Deep Learning Toolbox
・Image Processing Toolbox
・Control System Toolbox
・Optimizetion Toolbox
1. 姿勢推定(OpenPose使用)
ほぼほぼMathworksの公式ページ深層学習を使用した体の姿勢の推定からのコピペですが、著者の勉強の意味も込めて少し丁寧に解説していきます。
1.1 OpenPoseモデルの読み込み
ここは特に解説不要と思います。
(ただし、著者環境ではdownloadTrainedOpenPoseNetのパスが通っていないとのエラーが出たため該当する関数が格納されたフォルダをaddpathしています)
% 訓練済みOpenPoseモデルをDLし解凍
dataDir = fullfile(tempdir,'OpenPose');
trainedOpenPoseNet_url = 'https://ssd.mathworks.com/supportfiles/vision/data/human-pose-estimation.zip';
addpath('C:\Users\kuroda38\Documents\MATLAB\Examples\R2021a\deeplearning_shared\EstimateBodyPoseUsingDeepLearningExample');
downloadTrainedOpenPoseNet(trainedOpenPoseNet_url,dataDir);
unzip(fullfile(dataDir,'human-pose-estimation.zip'),dataDir);
% 不要な層を削除した上でネットワークとして指定
modelfile = fullfile(dataDir,'human-pose-estimation.onnx');
layers = importONNXLayers(modelfile,"ImportWeights",true);
layers = removeLayers(layers,["Output_node_95" "Output_node_98" "Output_node_147" "Output_node_150"]);
net = dlnetwork(layers);
上記にてnetにOpenPoseが読み込まれました。
1.2 画像を読み込み、ヒートマップを取得する
読み込む画像としては下記を用います。
画像ファイル名については、制御愛好家の皆様であれば言わなくても分かるかと思いますが「LPF.jpg」です。

(実際には顔を隠してはいません & 全身像を取り込んでいます)
close all;
figure(1);hold on;
im = imread("LPF.jpg");
imshow(im);
netInput = im2single(im)-0.5;% -0.5~0.5に変換
netInput = netInput(:,:,[3 2 1]);%RGB入れ替え
netInput = dlarray(netInput,"SSC");%Deep learning arrayオブジェクトに変換
heatmaps = predict(net,netInput,"Outputs","node_147");%147層目を取り出し
allHeatmaps = extractdata(heatmaps);%dlarray からのデータの抽出
最終行allHeatmapsには体の各部位のヒートマップが格納されています。
次節ではヒートマップに加工を施し、ラベリングをしていきます。
1.3 体の各部位の座標取得
今回の場合、ボード線図を書く上では頭~腰までの姿勢情報を用いるものとします。
OpenPoseでは体の各部位に対し0~17までの番号が割り振られています。
画像引用元:OpenPoseを使って、かめはめ波を撃ってみた
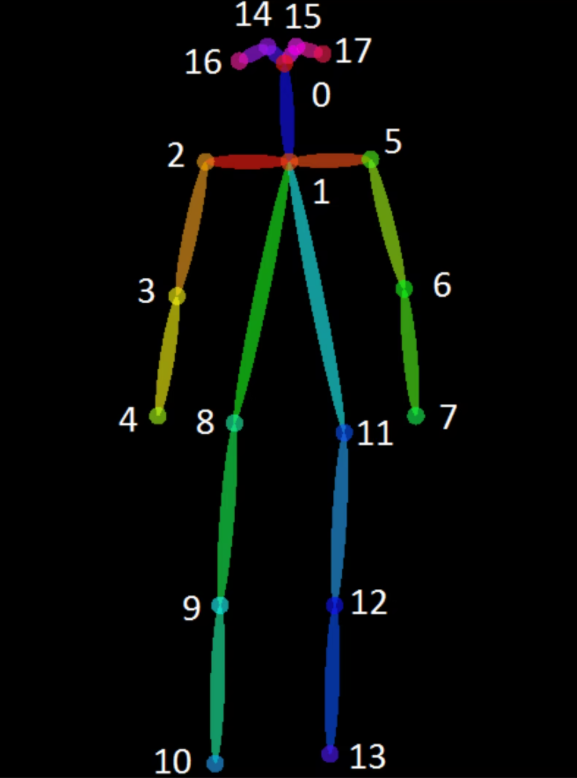
我らが誇るMATLABですが、インデックスは1から始まるのが俺のルール!という信念を曲げないため番号が1つずつずれます。
頭から腰までのヒートマップが欲しい場合、1~9,12が必要となります。
これらヒートマップを1つの画像に重ねて表示してみましょう。
imshow(sum(allHeatmaps(:,:,[1:9 12]),3));
それっぽく出来てますね。
次はラベリングしてみましょう。Image Processing Toolboxの関数regionpropsを使って各ヒートマップの重心および半径を求めます。ヒートマップはあくまで「画像の中で、体の各部位と思われる個所を抽出した結果」なので重心が複数得られる場合があります。この場合に対処すべく、半径が最大となる要素の重心を体の各部位の座標として処理を行っています。
コードやや長いので折りたたみます
imWidth = size(im,1); %元画像の横幅取得
imHeight = size(im,2); %元画像の高さ取得
heatmapWidth = size(allHeatmaps,1); %ヒートマップの横幅取得
heatmapHeight = size(allHeatmaps,2); %ヒートマップの縦幅取得
X = [];
Y = [];
figure(1);
imshow(im); hold on;
for i = [1:9 12] %抽出したいポイントの座標取得
heatmap = allHeatmaps(:,:,i);
heatmapBW = heatmap > 0.1;
heatmapStats = regionprops('table',heatmapBW,'Centroid',...
'MajorAxisLength','MinorAxisLength');
heatmapCenters = heatmapStats.Centroid;
heatmapDiameters = mean([heatmapStats.MajorAxisLength heatmapStats.MinorAxisLength],2);
heatmapRadius = heatmapDiameters/2;
[~, idx] = max(heatmapRadius);%直径の最大を持ってくる
xp = heatmapCenters(idx,1);
yp = heatmapCenters(idx,2);
X = [X; xp];
Y = [Y; yp];
xp_im = xp * imWidth / heatmapWidth;
yp_im = yp * imWidth / heatmapWidth;
text(xp_im, yp_im, num2str(i),'Color','red','FontSize',14);
end
 (Simulinkアイコンの下に「1」が表示されています)
ちゃんと体の各部位の座標が取れてますね。
(Simulinkアイコンの下に「1」が表示されています)
ちゃんと体の各部位の座標が取れてますね。
1.4 ボード線図っぽく表示する
上記体の部位のうち、右腕~胴~左腕、すなわち番号2から8までをボード線図と見立て、縦軸dB、横軸Hzのグラフ上に表示させます。
こちらもコードやや長いので折りたたみます
Xmin = min(X);
Xmax = max(X);
Ymin = min(Y);
Ymax = max(Y);
%2(胸)と9(腰)の距離を10倍および20Hzとして定義
V = [X(9) Y(9)] - [X(2) Y(2)];
baseDist = norm(V)/2;
XX = X(2:8).';
YY = Y(2:8).';
XXq = (Xmin:baseDist/20:Xmax).';
YYq = interp1(XX,YY,XXq);
plot(XXq,YYq,'b*')
Freq = 10 .^ (( XXq - Xmin ) / baseDist);
AngFreq = 2*pi*Freq;
Gain = -1 * ( YYq - Y(2) ) * 20 /baseDist;
figure();
semilogx(Freq,Gain);
grid on;hold on;
ボード線図っぽい感じに表示させる上で下記2つのポイントがあります。
ポイント①どのような姿勢が来ても縦横軸の大きさが安定するよう、2(胸)と9(腰)の距離を縦軸、横軸共通の基準距離として定義する
ポイント②ボード線図は横軸対数なので、画像における位置xをもとに 周波数=10^x として定義してsemilogxに突っ込む
ちょっとしたネタバレですが、ポイント①はこの後の伏線になっているので覚えておいて下さい。
2. 最適化を用いて伝達関数を求める
上記でとりあえずボード線図っぽいものは書けましたが、せっかく制御工学を学ぶのであれば得られた姿勢データをもとに伝達関数を求めるところまでやりたくなりますよね。
ということで、せっかくなのでやってみます。今回の場合、本人がLFPだと思ってポーズを取ったので伝達関数としてLPFが導出されれば完成となります。
2.1 最適化の準備
2.1.1 フィッティング対象関数
将来的にバンドストップフィルタないしバンドパスフィルタぐらいは体で表現ができるようにしておきたいので伝達関数は2次として定義します。
P(s)=\frac{b_2s^2+b_1s+b_0}{a_2s^2+a_1s+a_0}
上記式に含まれる6つのパラメータ(a0、a1、a2、b0、b1、b2)に対しフィッティングをかけます。
2.1.2 関数のmファイル化
伝達関数の各係数、および周波数ωを入力としてゲイン(dB)を返す関数をTFgen.mとしてmファイルで作成します。
function Gain = TFgen2(a0,a1,a2,b0,b1,b2,w)
Ps = tf([b0,b1,b2],[a0,a1,a2]);
%w = logspace(0,1000,100);
[mag,~] = bode(Ps,w);
Gain = 20 * log(squeeze(mag));
end
tfはControl System Toolboxの関数で、伝達関数の定義に用いています。
(こんなことでわざわざ使わなくても良いのだが、つい使ってしまうのが制御屋のサガ)
2.2 最適化の実施(fmincon使用)
誤差の二乗が最小になるよう最適化をかけます。
最適化の手法としては「とりあえずこいつ使っておけばええやろ」的な存在であるfminconを使いますが、思ったより良好な結果が得られなかったためパラメータの初期値は2通り準備しています。
efun = @(x) sum( ( TFgen(x(1),x(2),x(3),x(4),x(5),x(6),AngFreq) - Gain ).^2 );
% 最適化オプションの設定 出力関数outfunは後述する
options = optimset('Display','iter');%,'OutputFcn',@outfun);
x0_1 = [1, 1, 0, 1, 1, 0]; %最適化するa,bの初期値
x0_2 = [1, 1, 0, 1, 0, 0]; %最適化するa,bの初期値
lb = [1, -Inf, -Inf, -Inf, -Inf, -Inf];
ub = [Inf, Inf, Inf, Inf, Inf, Inf];
bestx1 = fmincon(efun,x0_1,[],[],[],[],lb,ub);
bestx2 = fmincon(efun,x0_2,[],[],[],[],lb,ub);
figure();
semilogx(Freq,Gain);
hold on;grid on;
GainOpt1 = TFgen(bestx1(1),bestx1(2),bestx1(3),bestx1(4),bestx1(5),bestx1(6),AngFreq);
semilogx(Freq,GainOpt1,'g*');
GainOpt2 = TFgen(bestx2(1),bestx2(2),bestx2(3),bestx2(4),bestx2(5),bestx2(6),AngFreq);
semilogx(Freq,GainOpt2,'r*');
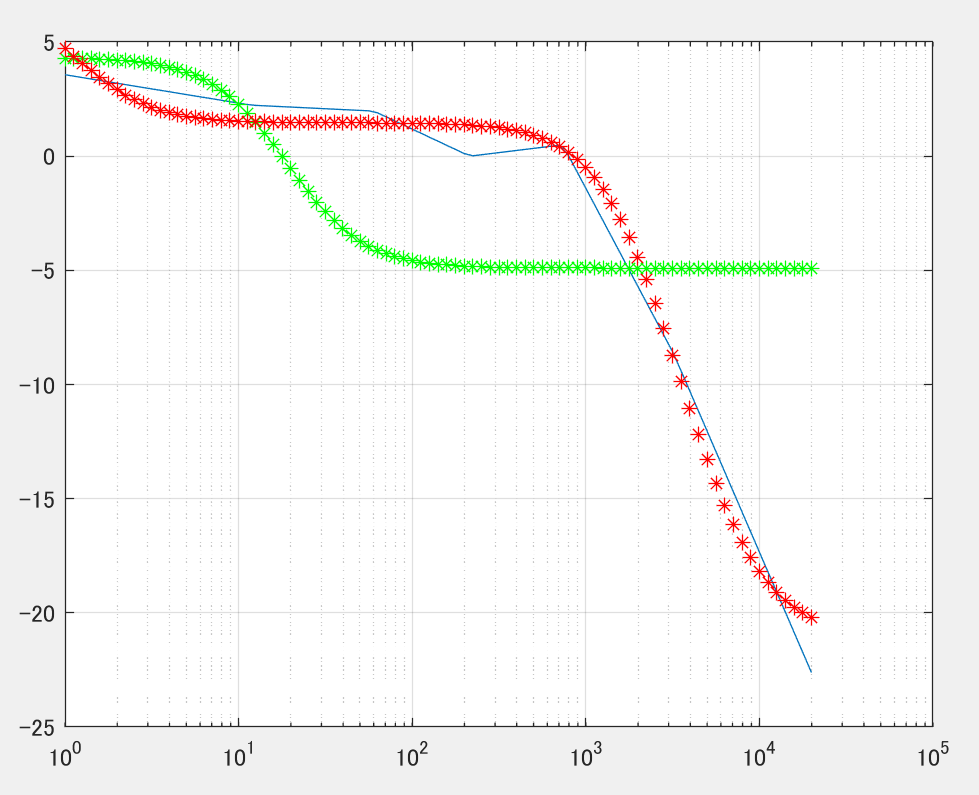
あれあれ…fminconさん…!?
緑は初期値をx0_1 = [1, 1, 0, 1, 1, 0]; とした場合、すなわち分子・分母ともに1次の伝達関数を起点として最適化をかけた結果ですが、あまり良好な結果になりませんでした。
赤は初期値をx0_2 = [1, 1, 0, 1, 0, 0];とした場合、すなわち分母のみ1次の伝達関数を起点とした場合ですが、結果的に分子も1次となる結果となりました。
いずれにせよ、得られたボード線図としては
P(s)=\frac{b_1s+b_0}{a_1s+a_0}
の形となってしまっており、LPFすなわち
P(s)=\frac{b_0}{a_1s+a_0}
を得ることが出来ませんでした。どうしてこうなった。
3. 所望の結果が得られなかった原因考察
fminconの設定を作りこむことでLPFに近づけていくことは可能ですが、今回の場合はそもそもの入力画像が良くなかったことが原因と考えられます。下記の画像をご覧ください。
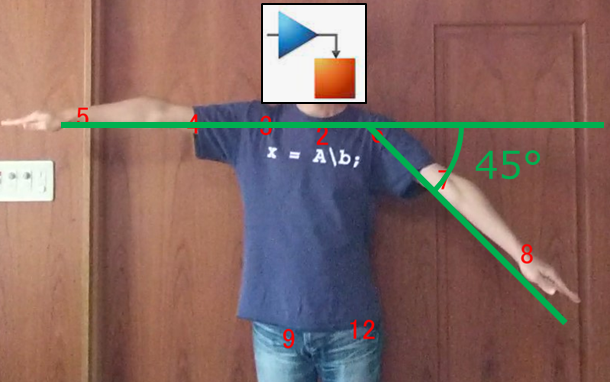
まず、左腕の角度が45度のつもりで45度になっていません。
これの何が問題かと言うと。
ポイント①どのような姿勢が来ても縦横軸の大きさが安定するよう、2(胸)と9(腰)の距離を縦軸、横軸共通の基準距離として定義する
上記定義を行ったため、写真における45°=20dB/decとなります。20dB/decって何?と思われたそこのアナタ、今こそボード線図の勉強をする時です。
LPFは1次遅れなので、カットオフ周波数以降のボード線図の傾きは必ず-20dB/decとなります。このため写真撮影時にきっちり45°にしておかないとLPFとして認識されなくなります。
加えて右手(5)の位置も、肩・腕のラインに対し水平になっていません。さらに言うと、右手(5)が水平より少し上の位置に来てしまったことによって伝達関数が
P(s)=\frac{b_1s+b_0}{a_1s+a_0}
の形に寄ってしまい、LPFとならなかったものと考察できます。
正直、この記事を書き始めたタイミングでは「LPFぐらいだったら簡単に出来るだろう」とタカを括っていたのですが、これら考察を通して改めて私自身がボード線図をカラダで分からせられる結果となりました。
4. 結論
MATLABでの姿勢推定は簡単なので、ぜひ皆さん試してみて下さい。
思い通りのボード線図をカラダで書きたければ、最適化の勉強よりもボード線図をしっかり勉強すると良さそうです。
お後がよろしいようで。