前回からChainerの基本オブジェクトについて,私が勉強したことを書いています.
今回はChainオブジェクトについて書いていきます.
#Chain
前々回はfunctionsオブジェクト,前回はlinksオブジェクトを紹介しましたが,今回のChainオブジェクトはそれらで提供される関数を合成してパラメータの推定を行います.その合成関数こそがモデルを表現しています.
まず,以下の図のような3層からなるニューラルネットワークを考えます.
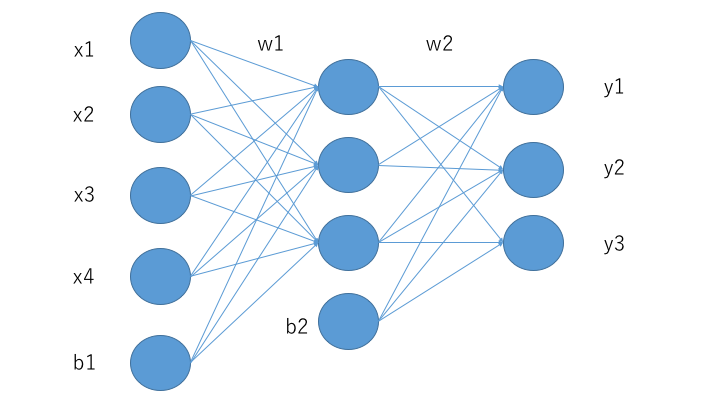
第1層から第2層への変換はlinksオブジェクトの際に紹介したように
v = w_1x + b_1 ...(1)
で表現することができます.(vは第2層時点での変数の状態)
次に,第2層から第3層への変換は
y = w_2v + b_2 ...(2)
で表現することができます.
(1)(2)より,第1層から第3層への変換は
y = w_2(w_1x + b_1) + b_2 ...(3)
で表すことができます.
しかし,第2層には活性化関数をそれぞれのノードで適応する必要があります.
よって,(3)は
y = w_2δ(w_1x + b_1) + b_2
と表現されます.(δは活性化関数)
この関数はfunctionsとlinksの関数で表現することができます.
そのためにChainクラスを用います.
ここではChainクラスを継承したMyChainを使います.
まず,コンストラクタにて層から層への写像をlinksの関数によって列挙します.
class MyChain(Chain):
def __init__(self):
super(MyClass, self).__init__(
l1 = L.linear(4, 3),
l2 = L.linear(3, 3)
)
そして,順方向の計算,すなわち活性化関数の処理をメソッドとして定義します.
def forward(self, x):
return F.sigmoid(self.l1(x)):
そして,損失関数(誤差関数)を__call__に書きます.mean_squqred_errorは二乗誤差関数です.
def __call__(self, x, y):
result = self.forward(x)
loss = F.mean_squared_error(result, y)
return loss
これで誤差の計算まで行うことができます.
今回はここまで.
次回はoptimizersについて書きます.
#参考
新納浩幸
Chainerによる実践深層学習~複雑なNNの実装方法~ オーム社