はじめに
混合ガウスモデルを、須山さんの本「ベイズ推論による機械学習入門」や確率モデル同士を結合し大規模なモデルを可能にするフレームワークであるSerketのコードを見ながら実行してみて、ようやくベイズ推論の意図するものが分かったので持論を展開したいと思います。
一般的なベイズ推定、ベイズ推論の理解
ベイズ推定は、Wikipediaに以下のように説明されています。
ベイズ推定(ベイズすいてい、英: Bayesian inference)とは、ベイズ確率の考え方に基づき、観測事象(観測された事実)から、推定したい事柄(それの起因である原因事象)を、確率的な意味で推論することを指す。
ベイズ推定それ自体については、この記事が分かりやすいです(上の文章はここから拝借しました)。また、ベイズ推論については、前述の本のほか、自由エネルギー原理についての非常に分かりやすい記事が参考になります。
ベイズ推論とは何か
私は下記のように解釈しています。
ベイズ推論とは、観測事象に対し、信念に基づく確率モデルを当てはめて、数学的に厳密にまたは近似的に、当該確率モデルの尤もらしいパラメータを求めること
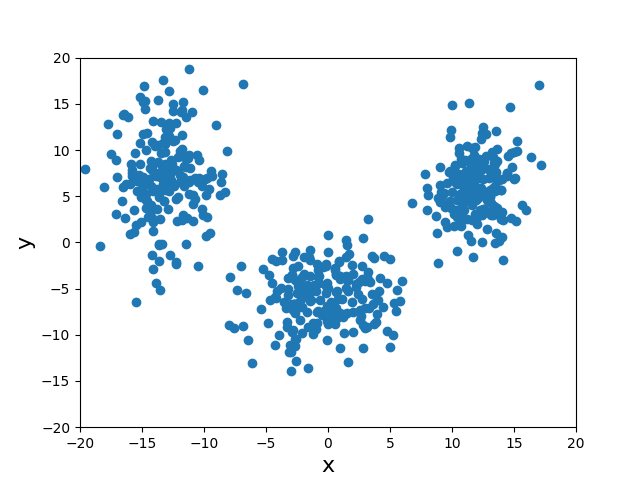
例えば、下記のような2次元データがあったとします(画像はここから拝借しました)。
いかにも2次元正規分布によって近似できそうです。実際、混合ガウスモデルによりクラスタをきれいに分けることができます。しかし、混合ガウスモデルでは、当然、事前分布としてガウス分布を想定しますが、これはただの信念でしかないのです。混合ガウスモデルではなくベイズ推論として広く考えれば、別にポアソン分布でもいいし、他の分布でも良いのです。
数式やコードや見栄えの良い図やグラフに惑わされがちですが、本質的には自らが考えた確率モデルに対して、無理やり観測データを当てはめて、最も都合の良いパラメータを計算させているのが、ベイズ推論の行っていることだと考えられます。
だからこそ、近似推論である変分推論を行ったり、いろんな近似を行ったり、解析的に解くことができない分布からサンプリングして値を求めて良いのです。
とはいえ、ベイズ推論は有用であることには変わりありません。なにせ、自分の考えたモデルに都合の良いパラメータを求めることにより、観測データの予測や分類が可能となるからです。近年では、脳内における計算においてもベイズ推論が行われていると言われており、計算論的神経科学や計算論的精神医学などといった分野も盛り上がりを見せています。
人間の思考の本質もベイズ推論なのかもしれません。
まとめ
ベイズ推論とは、観測事象に対し、信念に基づく確率モデルを当てはめて、数学的に厳密にまたは近似的に、当該確率モデルの尤もらしいパラメータを求めること
以上です。