須山敦志著の『ベイズ推論による機械学習入門』の第4章を読みました。4.4章 ガウス混合モデルにおける推論 をpythonで実装してみました。全コードは私のgitにあります。
記号の使い方
小文字の太字は縦ベクトル、大文字の太字は行列は表します。
多次元ガウス分布
$D$次元ガウス分布を、平均パラメータベクトル$\boldsymbol{\mu}\in \mathbb{R}^D$, 共分散行列${\bf \Sigma}\in \mathbb{R}^{D \times D}$を用いて
$$
{\mathcal N}({\bf x}|\boldsymbol{\mu},{\bf \Sigma})=\frac{1}{\sqrt{(2\pi)^D|{\bf \Sigma}|}} {\rm exp} \left\{ -\frac{1}{2}({\bf x}-\boldsymbol{\mu})^{\rm T}{\bf \Sigma^{-1}({\bf x}- \boldsymbol \mu)} \right\}
$$
で定義します。簡略のために精度行列${\bf \Lambda}={\bf \Sigma}^{-1}$を用います。
ウィシャード分布
$D\times D$の正定値行列${\bf \Lambda}$を生成するウィシャード分布を$D\times D$の正定値行列${\bf W}$を用いて次で表す。
$$
{\mathcal W}({\bf \Lambda}|\nu,{\bf W})= N |{\bf \Lambda}|^{\frac{\nu-D-1}{2}}{\rm exp}\left( -\frac{1}{2}{\rm Tr}({\bf W}^{-1}{\bf \Lambda}) \right)
$$
$N$は規格化定数で、パラメータ$\nu$は$\nu>D-1$を満たす。
カテゴリ分布
1 of K ベクトル${\bf s}$を生成するカテゴリ分布を次で表す。
$$
\rm{Cat}({\bf s}|\boldsymbol \pi) = \prod_{k=1}^K \pi_k^{s_k}
$$
ここで$\boldsymbol \pi= (\pi_1,\cdots , \pi_K)^{\rm T}$は分布を決めるパラメータで、$\pi_k \in (0,1)$かつ$\sum_{k=1}^K \pi_k = 1$を満たす。
ディレクレ分布
ベータ分布を多次元に拡張したディレクレ分布を次で表す。
$$
\rm{Dir}({\boldsymbol \pi}|\boldsymbol \alpha ) = N \prod_{k=1}^K \pi_k^{\alpha_k-1}
$$
ここで$N$は規格化定数で$K$次元のパラメータ$\boldsymbol \alpha$のそれぞれの要素は正の実数値です。ディレクレ分布は$\pi_k \in (0,1)$かつ$\sum_{k=1}^K \pi_k = 1$を満たす$\boldsymbol \pi$を生成する。
理論
詳細は『ベイズ推論による機械学習入門』の4.4章を読んでください。ここでは、前提と結論のみを書くに留めます。
前提
$K$個のガウス分布
\begin{align}
p({\bf x_n}|{\bf \mu}_k,{\bf \Lambda}_k) = {\mathcal N}({\bf x_n}|{\bf \mu}_k,{\bf \Lambda}_k^{-1})\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,k=1,2,\cdots,K
\end{align}
から$N$個のデータ${\bf X}=\{{\bf x_1},\cdots,{\bf x}_N\}$を得る。${\bf x}_n(n=1,2,\cdots,N)$は$D$次元のベクトル。$\boldsymbol{\mu}_k$,${\bf \Lambda}_k$は$k$番目のガウス分布の平均パラメータベクトルと精度行列であり、$\boldsymbol{\mu}_k\in \mathbb{R}^D$, ${\bf \Lambda}_k\in \mathbb{R}^{D \times D}$である。
ここで、各${\bf x}_n$がどのガウス分布によって生成されたのかを表現する$K$次元のベクトル${\bf s}_n$を導入する。${\bf x}_n$が$k$番目のガウス分布由来であるとき、${\bf s}_n$の第$k$成分$s_{n,k}$が$1$で、他の成分は$0$になる。ここで、$\boldsymbol{\mu}=\{\boldsymbol{\mu}_1,\cdots,\boldsymbol{\mu}_K\}$,$\boldsymbol{\Lambda}=\{\boldsymbol{\Lambda}_1,\cdots,\boldsymbol{\Lambda}_K\}$とすれば、さらに
\begin{align}
p({\bf x_n}|{\bf s}_n,{\bf \mu}_k,{\bf \Lambda}_k) = \prod_{k=1}^K {\mathcal N}({\bf x_n}|{\bf \mu}_k,{\bf \Lambda}_k^{-1})^{s_{n,k}}
\end{align}
以下のアルゴリズムの目的は、${\bf X}$から$\boldsymbol{\mu}$,${\bf \Lambda}$,${\bf S}$を求めることである。ただし${\bf S}=\{{\bf s}_1,\cdots,{\bf s}_N\}$である。
この観測モデルに対応する事前分布として、ガウス分布の共役事前分布であるガウス・ウィシャード分布を採用する。すなわち、ハイパーパラメータ${\bf m} \in \mathbb{R}^D,\beta \in \mathbb{R}^+,{\bf W} \in \mathbb{R}^{D\times D},\nu > D-1$を用いて
\begin{align}
p(\boldsymbol{\mu}_k,\boldsymbol{\Lambda}_k) = {\mathcal N}(\boldsymbol{\mu}_k|\boldsymbol{m},(\beta\boldsymbol{\Lambda}_k)^{-1}){\mathcal W}({\bf \Lambda}_k|\mu,{\bf W})
\end{align}
と書ける。なお、それぞれのクラスタの混合比率$\boldsymbol{\pi}=(\pi_1,\cdots,\pi_K)^{\rm T}$より${\bf s}_n$が決定する。
\begin{align}
p({\bf s}_n|\boldsymbol \pi) = {\rm Cat}({\bf s}_n|\boldsymbol \pi)
\end{align}
$p(\boldsymbol \pi)$はカテゴリ分布の共役事前分布であるディレクレ分布を用いて
\begin{align}
p(\boldsymbol \pi) = {\rm Dir}(\boldsymbol \pi|\boldsymbol \alpha)
\end{align}
と表現される。$\boldsymbol \alpha$はディレクレ分布のハイパーパラメータである。以上の議論をまとめて、モデル全体の設計図は以下の通りである。
\begin{align}
p({\bf X},{\bf S},\boldsymbol \mu,{\bf \Lambda},\boldsymbol \pi) &= p({\bf X}|{\bf S},\boldsymbol \mu,{\bf \Lambda})p({\bf S}|\boldsymbol \pi)p(\boldsymbol{\mu},\boldsymbol{\Lambda})p(\boldsymbol \pi) \\
&= \left\{ \prod_{n=1}^N p({\bf x_n}|{\bf s}_n,{\bf \mu}_k,{\bf \Lambda}_k)p({\bf s}_n|\boldsymbol \pi)\right\} \left\{\prod_{k=1}^K p(\boldsymbol{\mu}_k,\boldsymbol{\Lambda}_k)\right\} p(\boldsymbol \pi)
\end{align}
結論
以下のようなギブスサンプリングアルゴリズムが導出される。
\begin{align}
{\bf s}_n &\sim {\rm Cat}({\bf s}_n|\boldsymbol \eta_n) \\
{\bf \Lambda}_k &\sim {\mathcal W}({\bf \Lambda}_k | \hat{\nu}_k,\hat{{\bf W}}_k) \\
\boldsymbol \mu_k &\sim {\mathcal N}(\boldsymbol \mu_k | \hat{\bf m}_k,(\beta{\bf \Lambda}_k)^{-1}) \\
\boldsymbol \pi &\sim {\rm Dir}(\boldsymbol \pi | \hat{\boldsymbol \alpha})
\end{align}
ここで
\begin{align}
\eta_{n,k} &\propto {\rm exp}\left(-\frac{1}{2} ({\bf x}_n-\boldsymbol{\mu}_k)^{\rm T} {\bf \Lambda} ({\bf x}_n-\boldsymbol{\mu}_k) +\frac{1}{2} {\rm log}|{\bf \Lambda}_k| + {\rm log} \pi_k \right) \\
\hat{\alpha_k} &= \sum_{n=1}^N s_{n,k} +\alpha_k \\
\hat{\beta}_k &= \sum_{n=1}^N s_{n,k} + \beta \\
\hat{\nu}_k &= \sum_{n=1}^N s_{n,k} + \nu \\
\hat{{\bf m}}_k &= \frac{\sum_{n=1}^Ns_{n,k}{\bf x}_n+\beta{\bf m}}{\hat{\beta}_k} \\
\hat{{\bf W}}^{-1}_k &= \sum_{n=1}^N s_{n,k} {\bf x}_n{\bf x}_n^{\rm T} + \beta {\bf m} {\bf m}^{\rm T}-\beta_k {\bf m}_k {\bf m}^{\rm T}_k + {\bf W}^{-1}
\end{align}
である。
実装
まずは2次元ガウス混合モデルのギブスサンプリングを実装する。
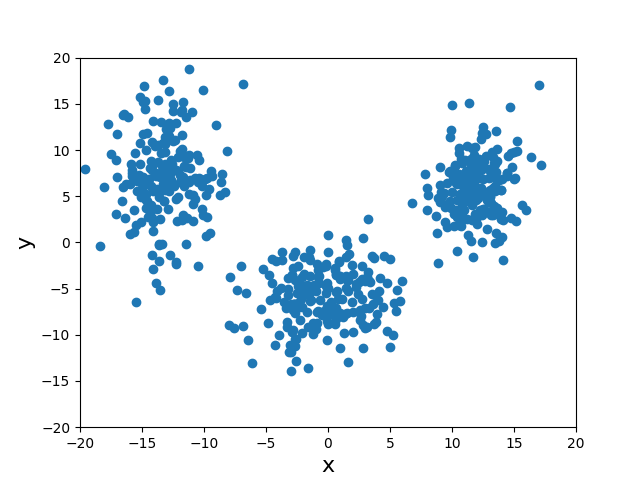
number_of_cluster$(=K)$種類の2次元ガウス分布からnumber_of_data$(=N)$個のデータを得る関数datasetを用意する。show_initialはTrueでnumber_of_data個のデータを2dplotする。正解となる平均ベクトルexpectation_vectors$(=\{\boldsymbol \mu_1,\cdots,\boldsymbol \mu_K\})$と共分散行列convariance_matrixs$(=\{{\bf \Lambda}^{-1}_1,\cdots,{\bf \Lambda}^{-1}_K\})$を設定する。デフォルトでnumber_of_cluster=3としているが、number_of_clusterを変化させる場合は、適宜、設定する。
def dataset(number_of_data,number_of_cluster,show_initial):
expectation_vectors = [[] for i in range(number_of_cluster)]
expectation_vectors[0] = [+12,+6]
expectation_vectors[1] = [0,-6]
expectation_vectors[2] = [-13,+7]
convariance_matrixs = [[[]] for i in range(number_of_cluster)]
convariance_matrixs[0] = [[3,1],[1,12]]
convariance_matrixs[1] = [[11,2],[2,9]]
convariance_matrixs[2] = [[5,0],[0,18]]
values = [[] for i in range(number_of_cluster)]
for k in range(number_of_cluster):
values[k] = np.random.multivariate_normal(expectation_vectors[k],convariance_matrixs[k],int(number_of_data/number_of_cluster))
data = np.vstack(values)
if show_initial:
plt.scatter(data[:,0],data[:,1])
plt.xlim([-20,20])
plt.ylim([-20,20])
plt.xlabel("x",fontsize=16)
plt.ylabel("y",fontsize=16)
plt.show()
return data
s_vector(=${\bf s}_n$)をカテゴリ分布からサンプリングする。eta[n][k]は$\eta_{n,k}$を意味する。
pi_vectorは${\boldsymbol\pi}$、predict_precision_matrixsとpredict_expectation_vectorsは予測された正解${\bf \Lambda},{\boldsymbol \mu}$を意味する。
def sampling_svectors(number_of_data, number_of_cluster, pi_vector, predict_precision_matrixs, predict_expectation_vectors):
eta = np.zeros((number_of_data,number_of_cluster))
for n in range(0,number_of_data):
for k in range(0,number_of_cluster):
eta[n][k] = math.exp(-0.5*(x[n] - predict_expectation_vectors[k] ) @ predict_precision_matrixs[k] @ (x[n] - predict_expectation_vectors[k] ) + 0.5*math.log(np.linalg.det(predict_precision_matrixs[k])) + math.log(pi_vector[k]))
for n in range(0,number_of_data):
normalized_const = 0
for k in range(0,number_of_cluster):
normalized_const = normalized_const + eta[n][k]
s_vectors[n] = np.random.multinomial(1,eta[n]/normalized_const)
return s_vectors
次にpi_vector($={\boldsymbol \pi}$)をディレクレ分布からサンプリングする。ここでsum2は$\sum_{n=1}^Ns_{n,k}$を意味する。
def sampling_pi_vector(number_of_data,number_of_cluster,s_vectors):
alpha_vector = np.ones(number_of_cluster)
new_alpha_vector = np.zeros(number_of_cluster)
for k in range(0,number_of_cluster):
sum2 = 0
for n in range(0,number_of_data):
sum2 = sum2 + s_vectors[n][k]
new_alpha_vector[k] = sum2 + alpha_vector[k]
pi_vector = np.random.dirichlet(new_alpha_vector)
return pi_vector
次に、predict_precision_matrixsとpredict_expectation_vectorsをウィシャード分布とガウス分布からサンプリングする。ただし、実際にウィシャード分布からサンプリングするのは大変そうだったので、ウィシャード分布の期待値$<{\bf \Lambda}>=\nu {\bf W}$を採用した。
def sampling_predict_precision_matrixs_and_predict_expectation_vectors(number_of_data,number_of_cluster,s_vectors,):
#ガウスウィシャード分布の超パラメータ
beta = 1.0
v = 2 # > D-1
m_vector = np.ones(2)
W_matrix = np.identity(2)
new_beta = np.zeros(number_of_cluster)
new_m_vector = np.zeros((number_of_cluster,2))
for k in range(0,number_of_cluster):
sum1 = 0
sum2 = 0
for n in range(0,number_of_data):
sum1 = sum1 + s_vectors[n][k]*x[n]
sum2 = sum2 + s_vectors[n][k]
new_beta[k] = sum2 + beta
new_m_vector[k] = (sum1 + beta*m_vector)/new_beta[k]
for k in range(0,number_of_cluster):
sum1 = 0
sum2 = 0
for n in range(0,number_of_data):
sum1 = sum1 + s_vectors[n][k]*(x[n].reshape(2,1) @ x[n].reshape(1,2))
sum2 = sum2 + s_vectors[n][k]
new_W_inverse = sum1 + beta*(m_vector.reshape(2,1) @ m_vector.reshape(1,2)) - new_beta[k]*(new_m_vector[k].reshape(2,1) @ new_m_vector[k].reshape(1,2)) + np.linalg.inv(W_matrix)
new_v = sum2 + v
predict_precision_matrixs[k] = new_v * np.linalg.inv(new_W_inverse)
predict_expectation_vectors[k] = np.random.multivariate_normal(new_m_vector[k],np.linalg.inv(new_beta[k]*predict_precision_matrixs[k]))
return predict_precision_matrixs,predict_expectation_vectors
二次元ガウス分布を返す変数を用意しておく。
def multivariate_Gaussian_distribution(x,y,precision_matrix,expectation_vector):
cordinate = np.array([x,y])
convariance_matrix = np.linalg.inv(precision_matrix)
return 1.0/((2.0*math.pi)**2*np.linalg.det(convariance_matrix))*math.exp(-0.5*(cordinate-expectation_vector)@np.linalg.inv(convariance_matrix)@(cordinate-expectation_vector))
求めた$\bf s$を用いてクラスタリングし、散布図をカラーリングして、等高線をひく関数を用意する。
def show_answer(number_of_data,number_of_cluster,x,s_vectors,predict_precision_matrixs,predict_expectation_vectors,show_contour):
groups = [[] for i in range(number_of_cluster)] #空の配列をnumber_of_cluster個用意する。
for n in range(0,number_of_data):
for k in range(0,number_of_cluster):
if s_vectors[n][k] == 1:
groups[k].append(x[n].tolist())
for k in range(0,number_of_cluster):
groups[k] = np.array(groups[k])
plt.scatter(groups[k][:,0],groups[k][:,1])
if show_contour:
N = 60
cordinate_x = np.linspace(-20,20,N)
cordinate_y = np.linspace(-20,20,N)
cordinate_X,cordinate_Y = meshgrid(cordinate_x,cordinate_y)
value_of_z = np.zeros((N,N))
for k in range(0,number_of_cluster):
for i in range(0,N):
for j in range(0,N):
value_of_z[j][i] = multivariate_Gaussian_distribution(cordinate_x[i],cordinate_y[j],predict_precision_matrixs[k],predict_expectation_vectors[k])
plt.contour(cordinate_X,cordinate_Y,value_of_z)
plt.ylim([-20,20])
plt.ylim([-20,20])
plt.xlabel("x",fontsize=16)
plt.ylabel("y",fontsize=16)
plt.show()
最後にmain関数を用意する。
if __name__ == "__main__":
number_of_cluster = 3 #クラスタの数
trial_times = 80 #サンプリングを行う回数
number_of_data = 600 #入力データ数
assert number_of_data % number_of_cluster == 0, "入力データ数をクラス数の倍数にしてください。"
show_initial = True #分類前の2次元データ分布を見るか否か。
show_contour = True #分類後に正解等高線を表示するか否か。
#初期化
predict_expectation_vectors = np.zeros((number_of_cluster,2))
predict_precision_matrixs = np.zeros((number_of_cluster,2,2))
for i in range(0,number_of_cluster):
predict_precision_matrixs[i] = np.identity(2)
pi_vector = np.ones(number_of_cluster)
s_vectors = np.zeros((number_of_data,number_of_cluster))
#データを渡す
x = dataset(number_of_data,number_of_cluster,show_initial)
#ギブスサンプリングを実行
for i in range(0,trial_times):
#sをサンプリングする。
s_vectors = sampling_svectors(number_of_data, number_of_cluster, pi_vector, predict_precision_matrixs, predict_expectation_vectors)
#predict_precision_matrixsとpredict_expectation_vectorsをサンプリングする。
predict_precision_matrixs, predict_expectation_vectors = sampling_predict_precision_matrixs_and_predict_expectation_vectors(number_of_data, number_of_cluster, s_vectors)
#pi_vectorをサンプリングする。
pi_vector = sampling_pi_vector(number_of_data, number_of_cluster, s_vectors)
#答えをプロット
show_answer(number_of_data,number_of_cluster,x,s_vectors,predict_precision_matrixs,predict_expectation_vectors,show_contour)
#最終結果を表示
print("Trial回数:",trial_times,"\n")
for k in range(0,number_of_cluster):
print("グループ"+str(k)+"の平均\n",predict_expectation_vectors[k])
print("グループ"+str(k)+"の共分散行列\n",np.linalg.inv(predict_precision_matrixs[k]),"\n")
結果
2次元ガウス混合モデル
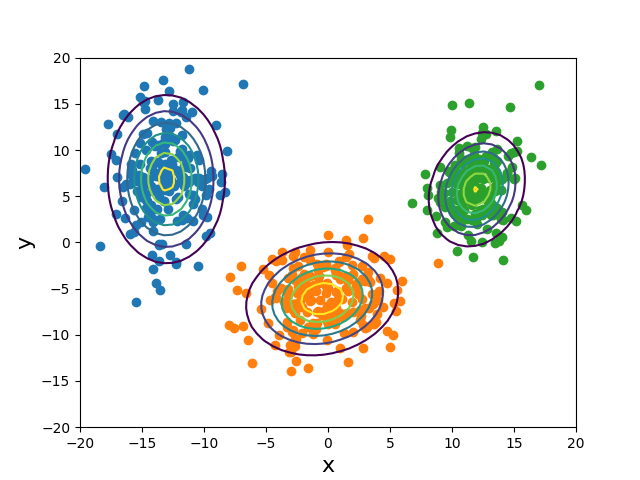
1枚目の画像の600点を3つのクラスタに分類した後の様子が2枚目である。80回で正しくクラスタリングされている様子が分かる。
グループ0の平均
[-13.03527306 6.85378566]
グループ0の共分散行列
[[ 5.55089831 -0.06026977]
[-0.06026977 20.82277496]]
グループ1の平均
[-0.46999732 -6.09191948]
グループ1の共分散行列
[[9.62733973 1.28850163]
[1.28850163 9.60439715]]
グループ2の平均
[12.0153539 5.74785767]
グループ2の共分散行列
[[3.78214067 1.07161246]
[1.07161246 9.74919818]]
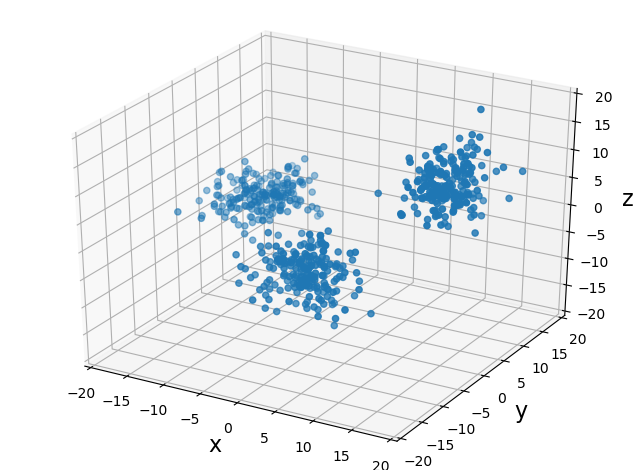
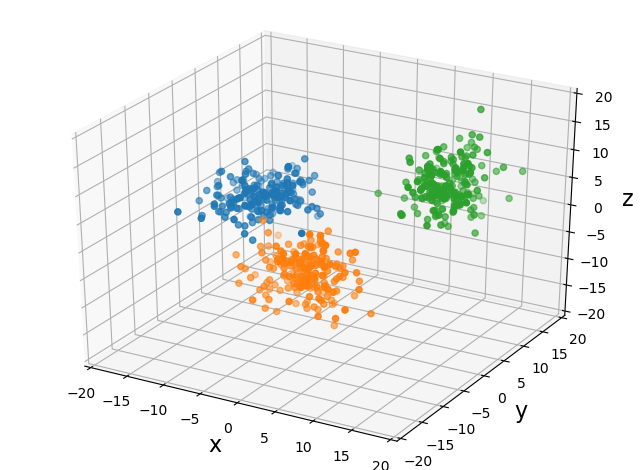
3次元ガウス混合モデル
3次元版でもやってみた!(ソースコードはこちら)