Quarto Pubに今回はスライド形式でpublishしてみました!!
markdownの原稿を以下に記載していますが、基本的にはスライドの方が読みやすい気がします...!! まあどちらでも:)
最近、MNARデータの扱いに興味があるので、次週もMNARデータに対処する論文を読みます...!(違うアプローチ)
上のハイパーリンクからでも良いですし、以下のlinkからでもスライドに飛べます.
論文の基本情報
- title: Recommendations as Treatments: Debiasing Learning and Evaluation
- published date: 17 Feb 2016,
- authors: Wondo Rhee, Sung Min Cho, Bongwon Suh
- url(paper): https://arxiv.org/abs/1602.05352
ざっくり論文概要
- 本論文は、推薦システムにおけるMNAR(Missing Not at Random)データを使った**学習 & 評価(検証)**において、因果推論の傾向スコアを用いて誤差関数を調整する事でbiasに対処しよう!という話だった.
- MNARデータに対する"学習のみ"や、"評価のみ"に焦点を当てた論文も多いが、本論文は両方に焦点を当てて汎用的なアプローチの提案を試みている印象.
- MNARデータを使ってそのままモデル性能(誤差関数)を推定しようとすると、真のモデル性能の値に対してbiasが発生してしまう. (不偏推定量でなくなってしまう.)
- そこで因果推論分野の**propensity score(傾向スコア)**を用いて、モデル性能の推定量を調整して、真のモデル性能の不偏推定量を作ろう...!!という話.
- ↑で作ったモデル性能の不偏推定量をモデル性能の評価(検証)や学習時の目的関数に使う事で、MNARデータにおいても良い感じの推薦モデルを作れる・選べるようになるぞ...!という話.
Introduction
推薦システムにおける選択バイアスとMNARデータ
- 推薦システムの学習用データ・検証用データは、実環境において多くの場合、選択バイアスがかかっている.
- ex.1) 映画推薦システムにおいて、ユーザは自分の好きな映画を観て評価し、自分の嫌いな映画を評価する事はほぼない. ->ユーザ自身の選択行動による選択バイアス
- ex.2) 広告配信システムにおいて、ユーザが興味を持ちそうな広告を表示するが、それ以外の広告を表示する頻度は低くなる. -> 推薦システムの動作による選択バイアス
- 様々な選択バイアスに伴い開発者が得られるのは、観測/未観測の傾向が偏ったデータ = **MNAR(Missing Not At Random)**と呼ばれるデータになる.(Little & Rubin, 2002)
本論文の目的 & アプローチの概要
- 本論文の目的は、選択バイアスによるMNARデータの元で、原理的、実用的かつ効果的に推薦システムを評価(検証)・学習できるアプローチを開発する事.
- 推薦を因果推論の観点から見ると、推薦システムでユーザにアイテムを見せることは、医学研究において患者に治療法を見せるのと同じような介入(intervention)である.
- 推薦と実験・観測データに対する因果推論を結びつけることで、選択バイアス下での推薦システムの公平な評価と学習のための原則的なフレームワークを導き出す.
MNARデータが従来の学習・検証に与える影響
映画の例の説明1
映画の例で、選択バイアスが従来の評価に与える悲惨な影響について考えてみる.
$u \in {1,...,U}$をユーザidx、$i \in {1,...,I}$ を映画idxとする.
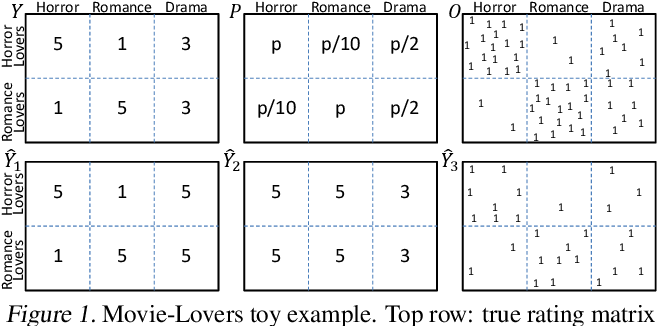
- 図1 左上の$Y$は、"ホラー好き"ユーザ集合は全てのホラー映画を5点、全てのロマンス映画を1点と評価する様な真の評価行列 $Y \in \mathbf{R}^{U \times I}$ ("ロマンス好き"ユーザ集合は逆)
映画の例の説明2
- 図1 右上のbinary行列 $O \in {0, 1}^{U \times I}$ は実際に評価が観測された{u,i}ペア. $[O_{u,i} = 1] ⇔ [Y_{u,i} \text{observed}]$ を意味する. ($O$はobservationの意味)
映画の例の説明3
- 図1 中央上の行列 $P$は、各{u,i}の評価が実際に観測される確率 $P_{u,i} = P(O_{u,i} = 1)$ を意味する. この映画の例では、映画ジャンルの好き嫌いと評価値の観測されやすさに強い相関がある。
映画の例の説明4
このデータについて、以下の二つのタスクの評価を考えてみる.
- タスク1: 評価値の予測精度の推定
- タスク2: 推薦の精度の推定
タスク1: 評価値の予測精度の推定
- 図1の左下 $\hat{Y}_1$ と中央下 $\hat{Y}_2$は、ある推薦モデル1と2によって予測された評価行列を表す。
タスク1では,これらの予測された評価行列 $\hat{Y}$が,真の評価行列$Y$をどれだけ反映(予測)できたかを推定(評価)したい...!
タスク1: 評価値の予測精度の推定
標準的なaccuracy metricの場合、次のように書くことができる.
$$
R(\hat{Y}) = \frac{1}{U \cdot I} \sum_{u=1}^{U} \sum_{i=1}^{I} \delta_{u,i}(Y, \hat{Y})
\tag{1}
$$
ここで、$\delta_{u,i}(Y, \hat{Y})$ は真の値と予測値の差を表し、具体的な $\delta()$ 関数は採用するmetricによって異なる.
しかし実環境では真の評価行列$Y$は一部の要素しか観測されない為、従来は以下の様に、観測済みエントリ{u,i}のみを用いて$R(\hat{Y})$を推定する.
$$
\hat{R}{naive}(\hat{Y})
= \frac{1}{|{(u,i):O{u,i} = 1}|} \sum_{(u,i):O_{u,i}=1} \delta_{u,i}(Y,\hat{Y})
\tag{5}
$$
これを、誤差関数 $R(\hat{Y})$ のnaive推定量と呼ぶ. このnaiveさが、図1の$\hat{Y}_1$、$\hat{Y}_2$に対する重大な誤判定を招いてしまう.
タスク1: 評価値の予測精度の推定
図1の例を見ると、$\hat{Y}_1$ の方が $\hat{Y}2$ よりも予測精度が優れているはず.
しかしnaive推定量$\hat{R}{naive}(\hat{Y})$は、$\hat{Y}_2$の方が予測誤差が小さいと判断してしまう...
これは選択バイアスによるものであり、1点の評価は観測されにくい為、誤差関数のnaive推定量では過小評価される。
より一般的に言えば、選択バイアス(MNARデータ)下では、naive推定量は真の誤差関数の不偏推定量ではない(Steck, 2013). すなわち:
$$
E_{O}[\hat{R}_{naive}(\hat{Y})] \neq R(\hat{Y})
\tag{6}
$$
タスク2: 推薦の精度の推定
タスク2では、予測評価値の精度ではなく、より直感的に推薦するか否かの意思決定の精度を評価する.
この為に$\hat{Y}$を再定義し、図1 右下の $\hat{Y}3$ では、$O$ に類似したbinary行列として推薦結果を符号化している. ここで、$[\hat{Y}{u,i} = 1]$ ⇔ [i が u に推薦される]とし、1ユーザあたりk件のみ推薦する.
タスク2: 推薦の精度の推定
推薦の精度を評価するmetricsとして一般的なのは、ユーザが推薦された映画から得るCumulative Gain(累積利益, CG). 図1の例では、推薦映画リストの平均評価として定義する.
以下の $delta()$ を用いて、再び式(1)の誤差関数を定義する事ができる.
$$
CG: \delta_{u,i}(Y, \hat{Y}) = (I/k) \hat{Y} \cdot Y_{u,i}
\tag{7}
$$
- しかし、ユーザが$\hat{Y}$の全ての映画を視聴していない限り、式(1)を用いて直接CGを計算することはできない. (真の目的関数は計算できない。観測データから近似する他ない...)
- 従って、実際に観測された映画を見ていた(消費した)代わりに、推薦$\hat{Y}$に従って映画を消費した場合、ユーザは(CGの面で)どの程度楽しめただろうか、という反実仮想的な問いに直面する.
- CGの様に推薦結果を集合を見なすmetricだけでなく、割引累積利益(DCG)、DCG@k、Precision at k(PREC@k)などのranking metricsも同様の設定が当てはまる.
タスク1と同様に式(5)のnaive推定量を用いる方法もあるが、タスク2においてもnaive推定量は$R(\hat{Y})$の不偏推定量ではない.
推薦システムの誤差関数の推定量をどのように不偏にする??
因果推論のアプローチを使ってみようという話
$Y$の観測値が欠損している状況で推薦システムの性能の不偏推定値を得る為に、本論文では、因果推論のaverage treatment effectsの推定方法を活用するアプローチを採用する.
推薦タスクを、ある薬で患者を治療するような介入(intervention)と同様に考えると、新しい治療方針(ex. 女性には薬Aを、男性には薬Bを与える = 新しい推薦結果$\hat{Y}$) の効果を推定したい.
どちらの場合も、ある患者(i.e. ユーザ)がある治療(i.e. 映画)からどれだけ恩恵を受けたかについては部分的な知識しかなく(すなわち、$O_{u,i} = 1$の $Y_{u,i}$のみ...!)、$Y$における潜在的な結果の大部分は未観測である、という課題がある.
選択バイアスを処理する鍵
選択バイアスを処理する鍵は、Observed Matrix $O$の観察パターンを生成するプロセスを理解することにある.
このプロセスは、一般的に因果推論におけるAssignment Mechanism、欠損データ分析におけるMissing Data Mechanismと呼ばれる.
2種類の観察パターン生成プロセス
論文では"観察パターン生成プロセス"を理解する為に、以下の2つの設定を区別して考える.
- Experimental Setting: "観察パターン生成プロセス"が推薦システムの制御下にある設定. ex. 広告配信システムは、どの広告をどのユーザに見せるかを完全に制御する.
- Observational Setting: "観察パターン生成プロセス"の一部にユーザの意志が含まれる設定. ex. 映画のオンライン配信では、ユーザが視聴する映画を自分で選ぶ.
Propensity Score(傾向スコア)を使って推定量を調整する
- 本論文では、"観察パターン生成プロセス"が確率的であると仮定する.
(i.e. 任意のユーザ-アイテムペアの評価値 $Y_{u,i}$ を観察する周辺確率 $P_{u,i} = P(O_{u,i} = 1)$ は非ゼロである.)- -> 真の評価行列 $Y$ の全ての要素が観察され得る、という仮定...!
- $P_{u,i}$を「$Y_{u,i}$ を観察する傾向(propensity)」と呼ぶ.
- Experimental Settingの場合、"観察パターン生成プロセス"は推薦システムの制御下にあるので、開発者はpropensity matrix $P$の全ての要素を把握できる.
- Observational Settingの場合、$P$ を observed matrix $O$ から推定する必要がある.
(observational settingに必要な) propensity $P$の推定の議論は後回しとし、まずはexperimental setting($P$が明らかになっているケース)に焦点を当てる.
Experimental Settingにおいて、どうMNARデータのbiasに対応する?
IPS(Inverse-Propensity-Scoring) 推定量
推薦タスクや予測タスクにも適用されるInverse-Propensity-Scoring (IPS)推定量 (Thompson, 2012; Little & Rubin, 2002; Imbens & Rubin, 2015) は、次のように定義される(名前通り、propensityの逆数を乗じてscoringしてる...!):
$$
\hat{R}{IPS}(\hat{Y}|P) = \frac{1}{U \cdot I} \sum{(u,i):O_{u,i} = 1} \frac{\delta_{u,i}(Y, \hat{Y})}{P_{u,i}}
\
= \frac{1}{U \cdot I} \sum_{u} \sum_{i} \frac{\delta_{u,i}(Y, \hat{Y})}{P_{u,i}} \cdot O_{u,i}
\
\because O_{u,i} \text{は観察されたか否かのbinary変数なので...!}
\tag{10}
$$
naive推定量 $\hat{R(\hat{Y})}_{naive}$ とは異なり、IPS推定量はあらゆる確率的な"観察パターン生成プロセス"において不偏推定量である. (正しい $P$さえ分かっていれば...!)
experimental settingの場合は真の$P$が分かるので、IPS推定量を活用できる.
(補足)IPS推定量の不偏性が実際の観測行列$O$に影響されない話
IPS推定量は周辺確率$P_{u,i}$のみを必要とし、その不偏性は 実際の観測結果 $O$ には影響されない.
(証明)$O$に対するIPS推定量の期待値を算出してみる.
$$
E_{O}[\hat{R}{IPS}(\hat{Y}|P)]
= \frac{1}{U\cdot I} \sum{u} \sum_{i}
E_{O_{u,i}}[\frac{\delta_{u,i}(Y,\hat{Y})}{P_{u,i}} O_{u,i}]
\
= \frac{1}{U\cdot I} \sum_{u} \sum_{i}
\delta_{u,i}(Y,\hat{Y})
\
\because \text{propensityの定義より...} P_{u,i} = E_{O_{u,i}}[O_{u,i}]
\
= R(\hat{Y})
\tag{10.5}
$$
IPS推定量のばらつきを抑える為に...SNIPS推定量の活用
IPS推定量のばらつきを抑える手法として、制御変量(control variates)の利用がある(Owen, 2013).
IPS推定量に適用すると、$E_{O}[\sum_{(u,i):O_{u,i}=1} \frac{1}{P_{u,i}}]= U \cdot I$ となることがわかる.(これを使うと、IPS推定量の分散を低減できる...??)
これにより、以下のSNIPS(Self Normalized Inverse Propensity Scoring)推定量が得られる:
$$
\hat{R}{SNIPS}(\hat{Y}|P) = \frac{
\sum{(u,i):O_{u,i} = 1} \frac{\delta_{u,i}(Y, \hat{Y})}{P_{u,i}} % 分子=元のIPS推定量の式.
}{
\sum_{(u,i):O_{u,i}=1} \frac{1}{P_{u,i}} % 制御変量?
}
\tag{11}
$$
分子は元のIPS推定量の式. 分母は制御変量?
SNIPS推定量はIPS推定量よりも分散が小さいことが多いが、小さいバイアスを持っている.
Observational Settingにおいて、どうMNARデータのbiasに対応する?
Observational Settingの場合、前述した通り、propensity $P$ の推定から始める必要がある. ($P$を推定した後は、experimental settingと同様にIPS推定量やSNIPS推定量を使える.)
ここで重要なのは、我々は $P$ を完璧に推定する必要はない、という事である.
なぜなら我々は、$P$が一様であるという仮説に基づくnaive推定量よりも"良い(マシな)"$P$を推定できれば良いのである...!
(補足) $P$の推定が、誤差関数のIPS推定量に与えるバイアス
真の評価行列$Y$の各要素を観測する周辺確率を$P$とし、すべてのu, iに対して$\hat{P}_{u,i} > 0$となるようなpropensity推定量を$\hat{P}$とする.
$\hat{P}$ を用いたIPS推定量(10)のバイアスは、以下:
$$
bias(\hat{R}{IPS}(\hat{Y}|\hat{P})) = \sum{u,i} \frac{\delta_{u,i}(Y, \hat{Y})}{UI} [1 - \frac{P_{u,i}}{\hat{P}_{u,i}}]
\tag{15}
$$
propensity 推定モデルの活用
復習だが、ここでの我々の目的は、ユーザ$u$とアイテム$i$の評価値が観測される確率$P_{u,i}$を推定する事.
一般にpropensityは以下に依存している可能性がある.
- 観測可能な特徴量 $X$: ex. アイテムのUIへの表示頻度, etc.
- 観測不可能な特徴量 $X^{hid}$: ex. アイテムが友人によって推薦された,etc.
- 真の評価$Y$ : ユーザがアイテムを好きか嫌いか.
式にするとこう:
$$
P_{u,i} = P(O_{u,i} = 1| X, X^{hid}, Y)
\tag{17}
$$
続いて、2つのシンプルなpropensity推定モデルをざっと紹介するが、ドメイン固有のニーズに対応できる技法も幅広く存在する(例:McCaffrey et al, 2004)
propensity 推定モデル1: ナイーブベイズによる推定
この方法では、$P_{u,i}$ と $X$、$X^{hid}$ との間の依存関係が無視できると仮定することで、$P(O_{u,i}|X, Xhid, Y)$ を推定する.(かなりラフな推定...!)
この仮定により、以下のnaive bayes推定量が得られる:
$$
P(O_{u,i} = 1|Y_{u,i} = r) = \frac{P(Y=r|O=1)P(O=1)}{P(Y=r)}
\tag{18}
$$
- なおIPSとSNIPSの計算には、観測されたエントリ{u,i}のpropensityのみが必要なので、上式における$Y_{u,i}$は観測されたものとして扱うことができる.
- $P(Y=r|O=1)$とP(O=1)の最尤推定値は、MNARデータで観測された評価を数えることで得ることができる.(シンプルに割り算で推定できる?)
- しかし、$P(Y=r)$を推定するためには、MCARデータの少量サンプルが必要.(ここは更にひと工夫する必要がありそう...!)
propensity 推定モデル2: ロジスティック回帰による推定
- この方法はロジスティック回帰に基づくもので、因果推論分野でよく使われる(Rosenbaum, 2002).
- この方法の目的は、$O$ が $X^{hid}$ と $Y$ に独立となる様なモデルパラメータ$\phi$を見つける事. (i.e. $P(O_{u,i}|X, X_{hid}, Y) = P(O_{u,i}|X, \phi)$ を満たす様な$\phi$)
- 以下のモデル式を満たす様な$\phi = (w, \beta, \gamma)$が存在する、と仮定する.
$$
P_{u,i} = \sigma(w^T X_{u,i} + \beta_{i} + \gamma_{u})
$$
- ここで、$X_{u,i}$は、{u,i}ペアに関する全ての観測可能な特徴量をベクトル化したもの. $\sigma()$はsigmoid関数.
- $\beta_{i}$、$\gamma_{u}$は、それぞれアイテム毎、ユーザ毎にユニークなoffset項.
実験方法・結果
合成データを用いて、experimental setting と observational setting の両方で提案手法の経験的性能とロバスト性を探る.
また、実世界のデータセットにおいて、MNAR(Missing Not At Random)データに対する最先端の共同尤度法(Hernandez- ´ Lobato et al, 2014)と比較した.
実験方法
- 全ての実験において、行列因子分解モデル(MFモデル)を使用.(ハイパーパラメータは、正則化の強さを決める$\lambda$とベクトル次元数$d$)
- モデル性能の評価方法に関しては、実世界データセットの場合はMCARテストセット、合成データの場合は式(1)を用いた評価をする.
- 合成データにおいて、{u,i}ペアをサンプリングする事でMNARデータによる選択バイアスを再現する.
- $\alpha \in (0,1)$ を変化させる事で、選択バイアスの厳しさをコントロールする. ($\alpha = 1$ はMCARデータ. $\alpha =0$ は 4~5点の評価のみが観測される厳しめのMNARデータ)
実験1: 選択バイアスの厳しさは推薦モデルの検証にどう影響するか?
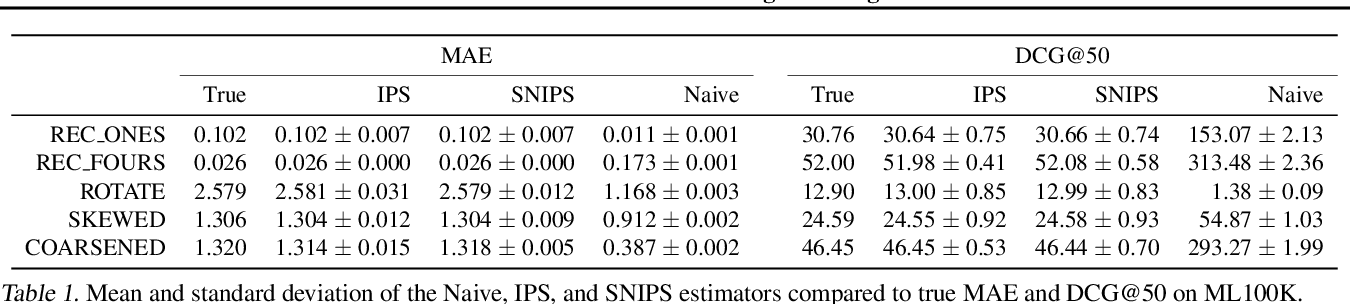
表1は、$\alpha = 0.25$ (=結構MNARなデータ)の場合のMAEとDCG@50の推定値の結果.
- IPS推定量の平均値は、MAEとDCGの両方で真の性能に完全に一致する.
- naive推定量は著しく偏り、推薦モデルの良し悪しの誤ったランク付けを導く.(ex. REC ONESの性能をREC FOURSよりも高くランク付けしてしまう.)
実験1: 選択バイアスの厳しさは推薦モデルの検証にどう影響するか?
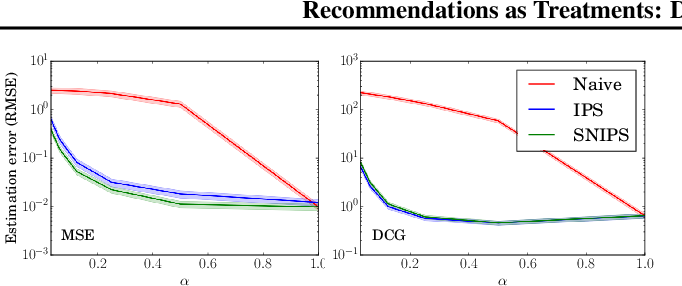
図2は、各推定量が"真のMSEとDCGをそれぞれどの程度正確に推定できたか"をRMSEを用いて表したもの.
- αのほとんどの範囲において、特に現実的な値であるα=0.25では、IPSとSNIPSの推定値はNaive推定値よりも桁違いに高い精度を示している.(真の誤差関数の値に対する精度...!)
実験2: 選択バイアスの厳しさは推薦モデルの学習にどう影響するか?
次に、このような誤差関数(=モデルの性能)の推定精度の向上が、ERMによる学習効果の向上につながるかどうかを、再びExperimental Setting で検証してみた.
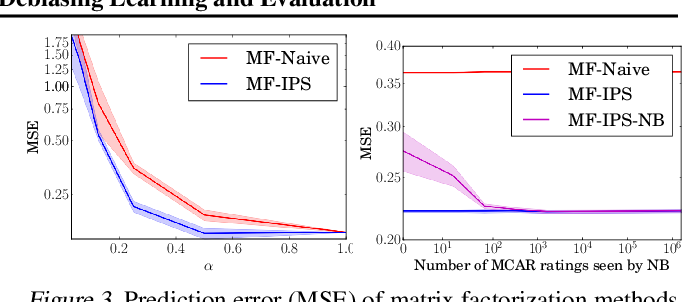
図3 左図は、MF-IPSとMF-naiveの真の予測性能(真の評価行列$Y$に対する誤差関数)をMSEで算出した結果. MF-IPSは従来のMF-naiveを常に上回る.
実験3: 不正確に学習されたpropensityに対して、評価や学習はどの程度ロバストなのか?
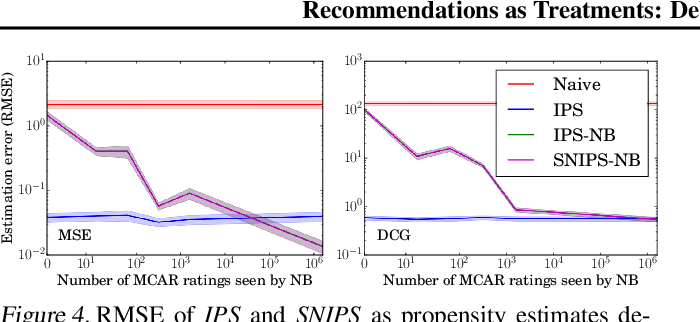
図4は、propensity推定が必要なObservational Settingにおいて、propensity 推定の不正確さが推薦モデルの検証にどのような影響を与えるかを示したもの. (propensity推定にはナイーブベイズを採用)
- 興味深いことに、propensities 推定したIPS-NBは、propensityが既知のIPS-KNOWNよりもさらに優れた性能を発揮した.
- 推定された propensities が層別化のような効果をもたらすこともあり、知られている効果らしい.(Hirano et al, 2003; Wooldridge, 2007)
実験3: 不正確に学習されたpropensityに対して、評価や学習はどの程度ロバストなのか?
また図3 右図は、propensity が不正確な場合に推薦モデルの学習にどのような影響があるかを示している.
propensitiyを推定したMF-IPS-NBのMSE予測誤差を、propensityが既知のMF-NaiveとMF-IPSと比較したもの.
ここでも、MF-IPS-NBは、著しく劣化した(MCARの観測データ数が少ない為...!)propensity推定値においてもMF-Naiveを上回り、本アプローチのロバスト性を実証している. (そもそもMF-naiveが超絶劣化したpropensity推定と見なせるから...!)
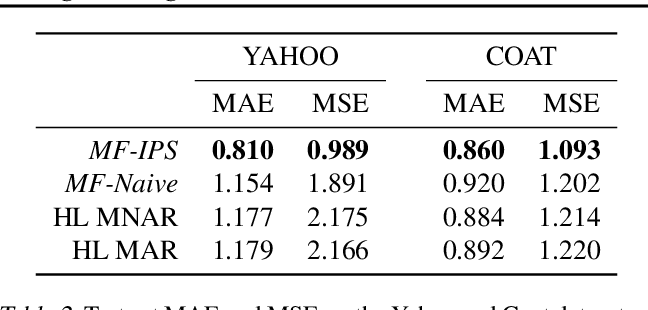
実験4: 実世界データにおける性能はどう?
MCARデータとMNARデータの両方を含んだベンチマークデータセットを用いて性能を評価(オンライン実験をした訳では無い).
MF-IPSにおいてpropensity推定はロジスティック回帰を用いた.
表2は、各推薦モデルのMCARテストセットに対する評価値の予測精度を評価したもの.
MF-IPSは、MF-naiveやHL-MNARやHL-MARを大幅に上回った.
更にMF-IPSの性能は、YahooデータセットのSOTAに近い結果だったとの事.
議論
- 提案したMF-IPSは、更に拡張が可能っぽい:
- propensity推定のための改良された手法を適用できる.
- propensity推定モデルと推薦モデル(rating予測モデル)を分離している為、実用的.
- -> 既存の推薦システムの運用において、propensity推定モデルを差し込むのみで良いので導入しやすい...??