はじめに, 本記事は論文読み会で発表した内容になります.
Managing Popularity Bias in Recommender Systems with Personalized Re-ranking
published date: 12 August 2019,
authors: Himan Abdollahpouri, Robin Burke, Bamshad Mobasher
url: https://arxiv.org/pdf/1901.07555.pdf
(勉強会発表者: morinota)
どんなもの?
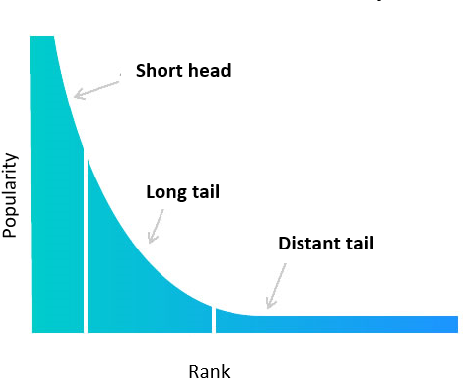
- 多くの推薦システムでは、人気のアイテム(="short-head"なアイテム)は頻繁に推薦され、人気のないニッチなアイテム("long-tail"なアイテム)はほとんどor全く推薦されないという、Popularity Bias(人気度バイアス)に悩まされている.
- もちろん人気アイテムを推薦する事が良いユーザ体験をもたらすケースもあるが、新しいアイテムの発見を促進せず、ニッチな嗜好を持つユーザーの興味を無視する事になる.
- 本論文では、推薦システムの出力(各ユーザへの推薦アイテムリスト)に後処理を追加する事で、推薦精度を維持しながらも推薦結果にshort-head & long-tailの多様性を持たせるアプローチを提案しています.
先行研究と比べて何がすごい?
- 他の多様性を向上させる手法 LT-Reg(regularized long-tail diversification algorithm)と比較して:
- 後処理的なアプローチの為、任意の推薦アプローチに対して適用可能.
- long-tail item promotionの度合いのパーソナライズ.
どうやって有効だと検証した?
以下の2種類の公開データセット(ベンチマーク)を用いている.
- Movielens 1Mデータセット:
- MovieLensユーザによる映画アイテムに対する評価(rating, feedback, reaction)値データ
- personalized recommendation分野では恐らく最も有名なデータセットですね...!
- Epinionsデータセット:
- ユーザがアイテムをレビューできる消費者意見サイトから収集されたもの.
- Movielens 1Mよりも疎なデータセット (i.e. ユーザ×アイテムの評価行列において、ゼロ要素の割合が多い.)
全ユーザに対して、以下の4種類の手法を用いてそれぞれ推薦アイテムリストを作成する. なお後者2つに関しては、ベースライン(RankALS)の推薦結果に対して後処理を行い、推薦リストを再構築している.
- RankALS: ベースラインとなる推薦アルゴリズム.
- LT-Reg(regularized long-tail diversification algorithm):
- Popularity Biasを考慮した推薦に関する既存研究の手法.
- Binary xQuAD: 本論文で提案されたアプローチの1つ.
- Smooth xQuAD: 本論文で提案されたアプローチの1つ.
精度の評価指標としてnDCG、推薦の多様性の評価指標として以下の3つを採用.
- Average Recommendation Popularity (ARP):
- 各推薦リスト内のアイテムの平均人気度.
- $ARP = \frac{1}{|U_t|} \sum_{u \in U_t} \frac{\sum_{i \in L_u} \phi(i)}{|L_u|}$
- 推薦リスト内の任意のアイテムについて、人気度の代理指標として、それらのアイテムの平均評価数を測定.
- Average Percentage of Long Tail Items (APLT):
- 推薦リストにおけるlong-tailアイテムの割合の平均値.
- $APLT = \frac{1}{|U_t|}\sum_{u \in U_t} \frac{|{i,i \in (L_u \cap \Gamma)}|}{|L_u|}$
- Average Coverage of Long Tail items (ACLT):
- 推薦システムがlong-tailアイテム達の何割をカバーしたかを測定する.
- $ACLT = \frac{1}{|U_t|} \sum_{u \in U_t} \sum_{i \in L_u} \mathbb{1}(i \in \Gamma)$
- APLTとの違い: (ex. 1種類のlong-tailアイテムを全ユーザに推薦しても、複数のlong-tailアイテムを1ユーザ一つずつ推薦したとしてもAPLTは値が等しくなってしまう.)
技術や手法の肝は?
情報検索の結果に多様性を持たせる手法である**xQuAD(EXplicit Query Aspect Diversification)**を応用し、推薦アルゴリズムにおけるPopularity Biasの制御(i.e 推薦結果がshort-tailアイテムのみにならないようにする.)を試みている.
本研究におけるxQuADモデルは、あるユーザー$u$への推薦リスト$R$を受け取り、以下の式による再スコアリングを行う事で、精度の損失を最小限に抑えつつ推薦アイテムの多様性が高まるような、最順位付けされた推薦リスト$S$ ($|S| < |R|$)を生成する.
$$
score = (1 - \lambda)P(v|u)+\lambda \sum_{c \in {\Gamma, \Gamma'}} P(c|u) P(v|c) \Pi_{i \in S} (1 - P(i|c, S)) \
\tag{4}
$$
ここで、
-
u, v: ユーザu, アイテムv
-
第一項 $P(v|u)$:
- ベース推薦アルゴリズムによって予測された値.
- ユーザ$u \in U$が、$V$内のアイテム$v $に興味を持つ尤度.
- (尤もらしさの尺度. スコアの大きさのスケールは各推薦手法に依存するだろうが、同じ推薦手法によるスコア間では、大きい程、uのvに対する嗜好度は高い.)
- 尤度: P(v)の確率分布のパラメータがuの時の、確率P(v)の値??
- 一般に、この値が高い順の上位n件が推薦リスト$R$に追加されている.
-
第二項 : long-tail多様性の為のボーナススコア:
- $\Gamma$, $\Gamma'$: long-tailのアイテム集合, short-headのアイテム集合.
- $P(c|u)$:
- ユーザuの過去のreactionのうち、アイテム集合cの占める割合.
- ユーザuの行動が、short-headアイテムばかりにreactionするタイプか, long-tailアイテムにも興味を示すタイプかを表現する.
- この項が、long-tail item promotionの度合いをパーソナライズする役割を果たす.
- $P(v|c)$:
- アイテムvがアイテム集合cに含まれる場合は1, そうでない場合は0を返すindicator function.
- $\Pi_{i \in S} (1 - P(i|c, S)) = P(S'|c)$:
- 「再順位づけ推薦リスト$S$にどの程度 アイテム集合cのitem達が不足しているか」の度合いを表す値.
- 本論文では、$(P(i|c, S))$の計算方法として、binary xQuADとsmooth xQuADの2つを提案している.
- binary xQuAD:
- smooth xQuAD:
-
直感的には、第1項はランキング精度を、第2項は2つの異なるカテゴリのアイテム(すなわち、short-tailとlong-tail)間の多様性を促進する.
-
$\lambda$:
- Popularity Biasをどの程度強く制御するかをコントロールするパラメータ.
- 大きく指定する程、long-tail多様性を考慮した推薦結果になる.
結果
議論はある?
先行研究の推薦多様性を向上させる手法 LT-Reg(regularized long-tail diversification algorithm)と比較して:
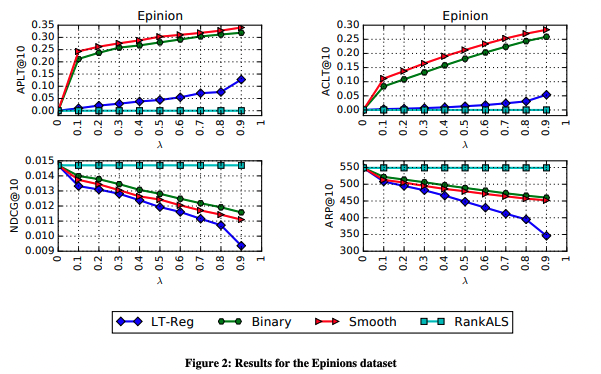
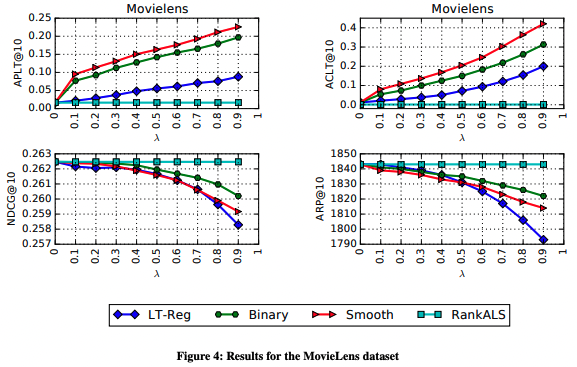
- ACLT指標の観点からは、xQuAD(特にsmooth xQuAD)は、正則化手法LT-Regよりもlong-tail多様性を向上させている.
- また、精度指標(nDCG)の低下もxQuADの方が抑えている.
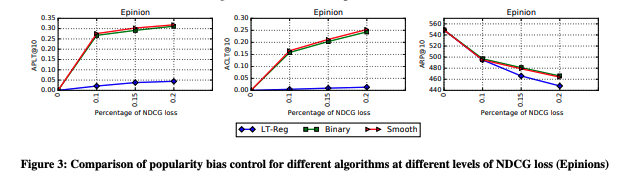
- xQuADの場合はハイパーパラメータの調整により、多様性と精度がトレードオフになる. 一方でLT-Regの場合は、精度を下げた時の多様性の向上度合いが小さい.
Binary xQuADとSmooth xQuADの違いに関して:
- 精度指標の低下は、binary xQuADの方が小さい. -> これは、一つ以上long-tailアイテムが含まれた時点で、再ランキングを辞めるから. つまり、元の推薦結果との差が小さい.
- smooth xQuADの方が、よりlong-tail多様性を高める事ができる.
推薦アイテム多様性の評価指標に関して:
- long-tailの多様性を測る評価指標として、ARPを単独で使用するのは不順分.
- 非常に似たARPパフォーマンスを持ちながら、long-tailアイテム達をカバーする能力と、long-tailアイテムをユーザに紹介する能力において、全く異なる場合がある.
- これらの指標をすべて一緒に見ることが重要.
次に読むべき論文は?
- 情報検索における検索結果多様化の先行研究Exploiting Query Reformulations for Web Search Result Diversification
- regularized long-tail diversification algorithmに関する論文 [Controlling Popularity Bias in Learning to Rank Recommendation](https://dl.acm.org/doi/10.1145/3109859.310991
実装するとしたら、なんとなくこんな感じ...?
import abc
from typing import List, Tuple
import numpy as np
import pandas as pd
class xQuADReranker(abc.ABC):
def __init__(
self,
base_user_item_scores: np.ndarray,
reaction_logs: pd.DataFrame,
lambda_param: float,
xquad_type: str = "binary",
) -> None:
"""コンストラクタ
Parameters
----------
base_user_item_scores : np.ndarray
元の推薦アルゴリズムから得られた、user*item対のスコア.
行indexがuser_id, 列indexがitem_idと対応している想定.
(実際には、{id:idx}のmappingが必要かも.)
reaction_logs : pd.DataFrame
過去のreaction log. user_id, item_id, createdの3つのカラムを持つ想定.
(pd.DataFrameが適切かは相談. 実行環境によってはList[dataclass]の方が良いかも.)
lambda: float
再ランキングのスコアリングに設定するパラメータ.
xquad_type: str
xQuADにおいてP(i|c, S)の計算方法の指定."binary" or "smooth"
"""
self.user_item_base_scores = base_user_item_scores
self.reaction_logs = reaction_logs
self.lambda_param = lambda_param
self.xquad_type = xquad_type
self.short_head_items, self.long_tail_items = self._devide_short_head_and_long_tail()
def _devide_short_head_and_long_tail(self) -> Tuple[List[int], List[int]]:
"""過去のreaction logを用いて、アイテム達をshort-headとlong-tailに分ける
返り値は、Tuple[List[short-head item ids], List[long-tail item ids]]
"""
pass
def rerank(
self,
user_id: int,
R: List[int],
S_size: int,
) -> List[int]:
"""あるユーザ(user_id)の推薦アイテムリスト(R)に対して、
long-tail多様性を考慮して、推薦アイテムがS_size個になるようにrerankingする.
"""
S = []
for _ in range(S_size):
candidates = [
(self.calc_score(user_id, item_id, S), idx) for idx, item_id in enumerate(R) if item_id not in S
]
_, idx = max(candidates, key=lambda t: (t[0], -t[1])) # スコアが同じならオリジナルのランキングに従う
S.append(R[idx])
return S
def calc_score(self, user_id: int, item_id: int, S: List[int]) -> float:
"""あるユーザのあるアイテムに対する、relank後のスコアを算出して返す."""
base_score = self.user_item_base_scores[user_id, item_id] # 論文におけるP(v|u)
divergence_bonus_score = 0.0
for c_group_items in [self.short_head_items, self.long_tail_items]:
c_group_reaction_ratio = self._calc_c_group_reaction_ratio(
user_id,
c_group_items,
) # 論文中のP(c|u)
is_item_in_c = 1.0 if item_id in c_group_items else 0 # 論文中のP(C|u)
c_shortage_in_s = self.calc_c_shortage_in_s(c_group_items, S)
divergence_bonus_score += c_group_reaction_ratio * is_item_in_c * c_shortage_in_s
return (1 - self.lambda_param) * base_score + self.lambda_param * divergence_bonus_score
def _calc_c_group_reaction_ratio(self, user_id: int, c_group_items: List[int]) -> float:
"""ユーザの過去のreactionのうち、
c_group_items(論文の場合はLong-tail/Short-headなアイテム)の占める割合
を計算して返す. ユーザの行動がアイテムの人気に素直に従っているか、それとも幅広くイロイロ触れるタイプか、
を表す. (long-tail promotionのパーソナライズの為.)
"""
pass
def calc_c_shortage_in_s(self, c_group_items: List[int], S: List[int]) -> float:
"""「現時点で S にはどの程度 c_group のitem達が不足しているか」を表すスコアを計算する.
論文中のP(S'|c) = \Pi_{i \in S} (1 - P(i|c, S)).
"""
c_shortage_in_s = 1.0 # 論文中のP(S'|c)の初期値
for item_in_s in S:
c_shortage_in_s *= 1 - self._calc_p_i_c_S(item_in_s, c_group_items, S)
return c_shortage_in_s
def _calc_p_i_c_S(
self,
item_id: int,
c_group_items: List[int],
S_items: List[int],
) -> float:
"""S中のitem iに対して, P(i|c, S)を計算して返す.
- binary xQuADの場合:
- P(i|c, S) = 1 if i in c else 0
- smooth xQuADの場合:
- P(i|c, S) = "リストSの中でCに属するアイテムの割合. (iは関係ない...?)"
"""
if self.xquad_type == "binary":
return 1.0 if item_id in c_group_items else 0.0
return (1.0 / len(S_items)) if item_id in c_group_items else 0.0