「量子アニーリングで計算するための初歩の初歩を考えてみた」の前回の投稿は、4つの量子ビットをつかって、最後に日立CMOSアニーラが使えるAnnealing Cloudを利用して、Isingモデルでアニーリングマシンへ計算を流してみました。日立のマシンは厳密には量子アニーリングではなく、CMOS(Complementary Metal Oxide Semiconductor:相補型金属酸化膜半導体)といわれる半導体で行うマシンです。
今回は、同じことをD-Waveでやってみようとおもいます。ただし、Isingではなく、せっかくなので、QUBO(Ouadratic Unconstrained Binary Optimization: 制約なし二値変数二次計画問題) 形式に変換をして行います。
D-Waveは、Ising も QUBOも受け付けてをしてくれますが、CMOSアニーラは、Isingのみとなります。
Isingとは、-1 or +1で表現していきますが、QUBOは 0 or +1 となります。この間は、たとえば、aという値をQUBOからIsingにするには、
$$ a_{ising} = 2a_{qubo} -1 $$
という式が成り立ちます。
実際に計算してみると
$a = 0$は、$ 2 * 0 - 1= -1$
$a = 1$は、$ 2 * 1 - 1= 1$
となります。
これとは、逆に、 IsingからQUBOにするには、そのまま式を計算すればよく、
$$ a_{qubo} = (a_{ising} + 1)/2 $$
という式になります。
$a = -1$は、$ (-1 + 1)/2 = 0$
$a = 1$は、$ (1 + 1)/2= 1$
となります。変換が可能です。
イジング模型として、エネルギーの状態をハミルトニアン$H$で次の方程式のように表しますが、
$$H = \sum J_{ij} \sigma_i \sigma_j + \sum_i h_i \sigma_i $$
$$\sigma_i = { +1, -1 } $$
同じように、QUBOは、
$$H = \sum Q_{ij} q_i q_j + \sum_i b_i q_i $$
$$q_i = { 0, 1 } $$
のように数式で書かれたたりすることがあります。
前置きが長なくなりましたが、D-Waveに乗せてみましょう。前回は、磁場項が0は−1、1は+1、2は-1、3は+1となっていたので、これ先ほどのIsingからQUBOにする式に代入すると、
$a = -1$は、$ (-1 + 1)/2 = 0$
$a = 1$は、$ (1 + 1)/2= 1$
は、QUBOでは、磁場項が0は0、1は1、2は0、3は1となります。
(※磁場項を0123でなくabcdにようにしておけばよかったと反省)
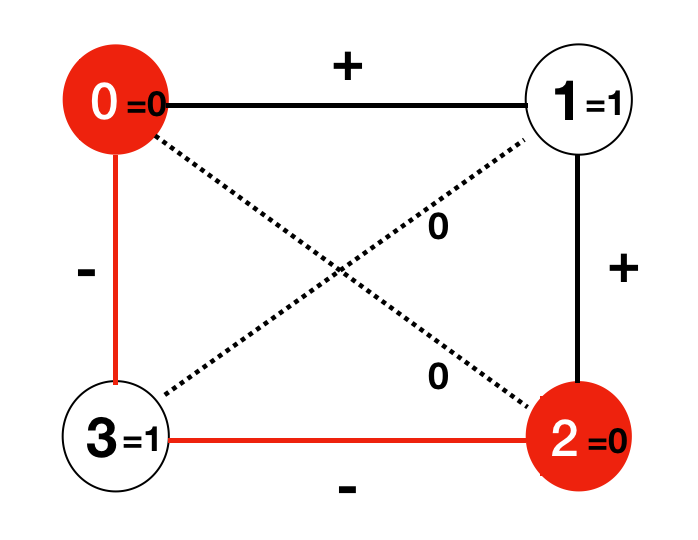
相互作用が0-1の間は+1, 1-2の間が+1, 2-3の間が-1, 0−3の間が−1で、対角線の0-2の間は0,1−3の間も0としてある。これを先ほどのハミルトニアンでの式で記述すると、
磁場項が、
$$ 1 * q_0 q_1 + 1 * q_1 q_2 -1 * q_2 q_3 + 0 * q_0 q_2 + -1 * q_0 q_3 + 0* q_1 q_3 $$
と、相互作用が
$$ 0 * q_0 + 1 * q_1 + 0 * q_2 + 1* q_3 $$
となり、整理すると、
$$ H = q_0 q_1 + q_1 q_2 - q_2 q_3 - q_0 q_3 \
- q_1 + q_3 $$
となり、これをアニーリングマシンへ放り込めば計算結果がでてくる仕組みとなっている。
行列をつくって、マシンに入れてあげればいい。
相互作用の項
---
0 0 0
1 1 +1
2 2 0
3 3 +1
---
磁場項の項
0 1 1
0 2 0
1 2 1
0 3 -1
1 3 0
2 3 -1
今回はせっかくなので、D-Waveにこれをいれて計算させてみましょう。
D-Waveのキメラグラフという特殊な形に載せる必要がありますが、今回の結合は、ビット間の結合をしないで、載せることが可能です。
モデル0番をD-wave4,モデル1番をD-wave2,モデル2番をD-wave6,
モデル3番をD-wave1のqbitとして、D-wave 4-2, 4-1の相互作用を+1 として、2-6と6-1を-1とすると、次の図となります。
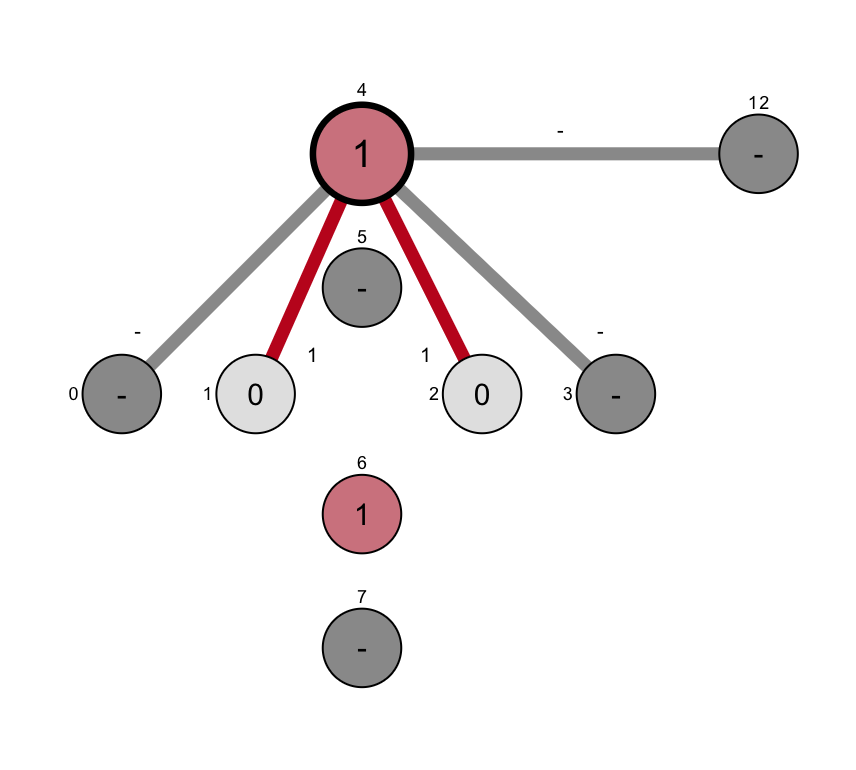

これの計算結果としては、100回計算して、


が戻ってきましたので、
D-Wave4(0) = 1
D-Wave2(1) = 0
D-Wave6(2) = 1
D-Wave1(3) = 0
で、エネルギーが -1 という結果になりました。とても簡単な問題なので、100回やっても同じ解が1つのみという素晴らしい結果です。

qpu_anneal_time_per_sample っていうのが実際にアニーリングを行なった時間で$20 \mu s $となっていました。これが計算が速いといわれるところになります。何をやってもだいたい$20 \mu s $です。
D-Waveの上記グラフでの計算は、モデルを理解するのにとても良いとおもうのですが、 1分間無料でつかえるD-Wave Leap
https://cloud.dwavesys.com/leap/signup/
では、このグラフは削除されていて、使うことができませんでした。
今日はこのくらいで。。。また次回。