量子コンピュータといろいろ世間で騒がれていますが、1982年にファイマンによって提唱されたもの(ゲート型)と、1998年に門脇、西森によって考えられた量子アニーリングっていうのがあります。量子アニーリングはやれることがとても限定的です。歴史的な説明は今後するとして、D-Waveが量子アニーリングをつかって本当に量子的な振る舞いを使って計算する機械を公開したっていうのが新しい扉を開けたと感じています。
D-WaveのLeapも日本から1分間つかえるし、HitachiのCMOSアニーラもAnnealing Cloud 経由で両方とも無料でつかえるので、本当にいい時代だとおもう。
量子アニーリングで計算するための初歩の初歩を考えてみたということで、本題に進んでいきます。量子アニーリングでは、イジング模型として、エネルギーの状態をハミルトニアン$H$で次の方程式のように表しますが、
$$H = \sum_{i<j} J_{ij} \sigma_i \sigma_j + \sum_i h_i \sigma_i $$
はじめのころは、これが全く何を言っているのか不明だった。
1、物理学的な意味
2、なんで量子アニーリングで計算できるのか?
の2点である。
1、物理学的な意味は、あまりわかっていない。一応、大学で量子力学の講義は受けて単位もらったけど、工学部で環境熱流体をやったので、そこまでちゃんとやっていないから、再度復習する必要があった。数冊量子力学の本を読んでみたが、このあたりはほとんど書いてないので、とりあえず、時間発展のハミルトニアンについてわかった気になって終わったというか、計算には物理学的な意味はあまり必要無いようにおもえる。ただし、知っていたほうがいいこともありそうなので、そのあたりはまた今度。
2、なんで量子アニーリングで計算できるのか、こっちがわからないと、アニーリングマシンで計算することができないので、ここでは簡単に説明していく。
$$H = \sum_{i<j} J_{ij} \sigma_i \sigma_j + \sum_i h_i \sigma_i $$
は、$\sum_{i<j} J_{ij} \sigma_i \sigma_j $ の相互作用項と、
$ \sum_i h_i \sigma_i $の磁場項の2つから成り立っている。
ここでは簡単に0、1、2、3の4個の量子ビットからなるモデルを考えてみる。
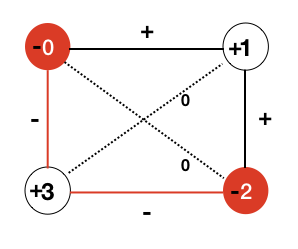
磁場項が0は−1、1は+1、2は-1、3は+1となっていて、相互作用が0-1の間は+1, 1-2の間が+1, 2-3の間が-1, 0−3の間が−1で、対角線の0-2の間は0,1−3の間も0としてある。これを先ほどのハミルトニアンでの式で記述すると、
磁場項が、
$$ 1 * \sigma_0 \sigma_1 + 1 * \sigma_1 \sigma_2 -1 * \sigma_2 \sigma_3 + 0 * \sigma_0 \sigma_2 + -1 * \sigma_0 \sigma_3 + 0* \sigma_1 \sigma_3 $$
と、相互作用が
$$ -1 * \sigma_0 + 1 * \sigma_1 -1 * \sigma_2 + 1* \sigma_3 $$
となり、整理すると、
$$ H = \sigma_0 \sigma_1 + \sigma_1 \sigma_2 - \sigma_2 \sigma_3 - \sigma_0 \sigma_3 \
- \sigma_0 + \sigma_1 - \sigma_2 + \sigma_3 $$
となり、これをアニーリングマシンへ放り込めば計算結果がでてくる仕組みとなっている。
どう放り込むか?というと、Ising -1 or 1 のモデルもしくはQubo 0 or 1のモデルで行列をつくって、マシンに入れてあげればいい。
相互作用の項
---
0 0 -1
1 1 +1
2 2 -1
3 3 +1
---
磁場項の項
0 1 1
0 2 0
1 2 1
0 3 -1
1 3 0
2 3 -1
というように、磁場項の方は量子ビットの番号と数値、相互作用の項は量子ビット間と数値 というようにあわらし、アニーリングマシンへ投げると結果が戻ってきます。
たとえば、これをHitachiのCMOSアニーラで公開されているannealing-cloudを
のイジングエディタで、上記をやってみると、
https://annealing-cloud.com/play/ising-editor.html

このような感じに設定して、 実行を押すと、結果が

こんな感じに戻ってくるということになります。
エネルギー(ハミルトニアン)は最低で−6(この場合は1つだったが複数出る場合がある)で、
0番 +1
1番 -1
2番 +1
3番 +1
の時にこのエネルギーが一番引く状態(基底状態)を得られたということになります。
これらを応用していくと、様々な問題を解くことが可能になるといったわけです。
今日のところはこのくらいで終了です。