PyQUBOでQUBOをつくって、そのままFujitsuデジタルアニーラへジョブ投入

量子をつかってなく、回路（FPGA,ASICなど）の専用回路をつかって、シミュレーションできるアニーリングマシンに、Fujitsuが作っているデジタルアニーラがあります。
APIの仕様など非公開なのかとおもっていたら、ドキュメントが富士通のサイトに上がっていたので、PyQUBOでQUBOをつくって、Fujitsuデジタルアニーラへjsonでジョブ投入する記事を書いてみます。

Fujitsuデジタルアニーラは、第一世代と第二世代があって、若干仕様が異なります。ユーザガイドは以下です。

また、オンプレミスサービスのユーザガイドは別のが用意されています。
https://www.fujitsu.com/jp/documents/digitalannealer/services/P3KD-1312.pdf

それでは、第一世代にPyQUBOでQUBOを作成し、WEB API経由で、jsonファイルをFujitsuデジタルアニーラへジョブ投入することを考えてみます。

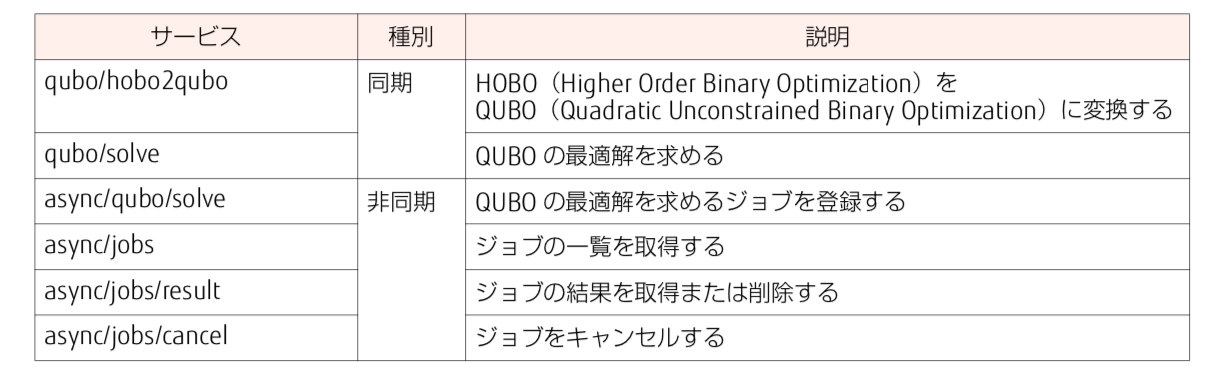
上記を良く読むことなりますが、今回はQUBOの最適解を求めるため、QUBO形式を同期形式でアニーリングマシンへジョブを送ることを考えてみます。これ以外HOBOや非同期でジョブのコントロールも可能です。
契約の状態によって使える部分が異なりますので、ジョブの投げ方には注意が必要です。

それでは、4個のうち１つを1にする問題を考えてみましょう。
詳細はn個のうちmだけを１にする問題をPyQUBOを使ってアニーリングマシンで解く問題 を参照ください。

式は、全部展開した
$$H=2(q0∗q1+q1∗q2+q0∗q2+q0∗q3+q1∗q3+q2∗q3)−(q0+q1+q2+q3)+1$$
を使ってもいいのですが、PyQUBOが

$$H = ( \sum_{i}^n q_{i} -m )^2 $$

のように２乗をそのまま記述することができるため、この式を使おうとおもいます。
そうすると、PyQUBOでの記述は、

# ハミルトニアンを記述　4個のうち1つを1にする
q1, q2, q3, q4 = Binary("q1"), Binary("q2"), Binary("q3"), Binary("q4")
H = (q1+q2+q3+q4-1)**2 

となります。これにより、QUBO形式つくることができるので、ここから作ったQUBOを、富士通デジタルアニーラの形式に変換して投げることになります。
富士通デジタルアニーラの QUBO形式にするには、ドキュメントによれば、

となっていますので、'coefficient': 2.0, と　'polynomials': [1, 2] の記述にする必要があり、
正規表現を利用して変換すれば可能です。

そのあと、json 形式を富士通デジタルアニーラ(1Qbit)のWEB API経由に投げ込めばレスポンスが戻ってきます。

from pyqubo import Binary
from pprint import pprint
import requests
import json
import re

#  Fujitsu DA acccess key
# ---------------------------
post_url = 'アクセスURLを記述/v1/qubo/solve'
post_headers = {'X-DA-Access-Key' : 'xxx アクセスキー　xxx', \
                   'Accept': 'application/json', \
                   'Content-Type': 'application/json'}
# ---------------------------

def req(ddic):
    #POSTパラメータは二つ目の引数に辞書で指定する 
    response = requests.post(post_url,
            json.dumps(ddic), \
            headers=post_headers)
    print(response.json())
    print(type(response.json()))
    return response

def qubodic_to_fdic(qdic, offset):
    # pyqubo x0, x1 to Fujitsu DA BinaryPolynomial
    fdic = {}
    gdic = {}
    alist = []
    for k, v in qdic.items():
        edic = {}
        a0 = re.sub(r'^[a-zAz]', '', k[0])
        a0 = re.sub(r'$', '', a0)
        a1 = re.sub(r'^[a-zAz]', '', k[1])
        a1 = re.sub(r'$', '', a1)
        edic["coefficient"] = v
        edic["polynomials"] = [int(a0), int(a1)]
        alist.append(edic)
    edic = {}
    edic["coefficient"] = offset
    alist.append(edic)
    gdic["terms"] = alist
    fdic["binary_polynomial"] = gdic 

    # ddicには fujitsuDAPTのパラメータを追加
    ddic ={"solution_mode":  "QUICK", \
               "number_iterations": 100, \ #色々なパラーメータがあり記述する
               }
    fdic["fujitsuDAPT"] = ddic #fujitsuDAPT, fujitsuDA2PT などがある。
    return fdic

# ハミルトニアンを記述　4個のうち1つを1にする
q1, q2, q3, q4 = Binary("q1"), Binary("q2"), Binary("q3"), Binary("q4")
H = (q1+q2+q3+q4-1)**2 


# Create QUBO
model = H.compile()
qubo, offset = model.to_qubo()

pprint(qubo)  ## QUBO形式の表示用
print(offset)
print("####################")

# Solve QUBO model by Fujitsu DA
# ---------------------------

fdic = qubodic_to_fdic(qubo, offset)  
pprint(fdic) #FujitsuデジタルアニーラのQUBO形式を確認
print("####################")
resdic = req(fdic) #jsonを送信

富士通デジタルアニーラでは、"solution_mode": に様々なモードがあり、これを調整することによって、解を得るスピードが格段に速くなったりするといわれているので、この部分の調整が不可欠です。

{('q1', 'q1'): -1.0,
 ('q1', 'q2'): 2.0,
 ('q1', 'q3'): 2.0,
 ('q1', 'q4'): 2.0,
 ('q2', 'q2'): -1.0,
 ('q2', 'q3'): 2.0,
 ('q2', 'q4'): 2.0,
 ('q3', 'q3'): -1.0,
 ('q3', 'q4'): 2.0,
 ('q4', 'q4'): -1.0}
1.0
####################
{'binary_polynomial': {'terms': [{'coefficient': 2.0, 'polynomials': [1, 2]},
                                 {'coefficient': 2.0, 'polynomials': [1, 3]},
                                 {'coefficient': 2.0, 'polynomials': [1, 4]},
                                 {'coefficient': 2.0, 'polynomials': [2, 3]},
                                 {'coefficient': 2.0, 'polynomials': [2, 4]},
                                 {'coefficient': 2.0, 'polynomials': [3, 4]},
                                 {'coefficient': -1.0, 'polynomials': [1, 1]},
                                 {'coefficient': -1.0, 'polynomials': [2, 2]},
                                 {'coefficient': -1.0, 'polynomials': [3, 3]},
                                 {'coefficient': -1.0, 'polynomials': [4, 4]},
                                 {'coefficient': 1.0}]},
 'fujitsuDAPT': {'number_iterations': 100, 'solution_mode': 'QUICK'}}
####################

ちゃんと契約をし、ジョブを投入することができると、このあとに、レスポンスが以下のような形で戻ってきます。

{'qubo_solution': {'result_status': True, 'solutions': [{'energy': 0, 'frequency': 1, 'configuration': {'1': False, '2': False, '3': True, '4': False}}], 
xxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxx
途中省略
xxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxx

今日はこのくらいで。

また、このプログラムはIPA未踏ターゲットで共同研究者石崎さんにアドバイスいただきありがとうございました。