感染症数理モデルの Python による解析はあるので、これを Javascript に書き直して数値シミュレーションしよう、という実験です。
ソフトウェア屋さんなので、思考実験しようというパターンです。
デモ
SEIR モデルを Python でシミュレートしている 感染症数理モデル事始め PythonによるSEIRモデルの概要とパラメータ推定入門 - Qiita のコードを Javascript に直しています。
元記事では、odeint を使って微分方程式を解く過程でのグラフを表示しています。Javascript 版は、odeint がないのと時間経過の中でパラメータを変更したかったので、1日進めながら各数値(S,E,I,R)を計算しています。
結果は、c3.js によってグラフ化、これは便利!!!
SEIR モデルの簡単な解説
Wikipedia だと、日本語版と英語版のボリュームが違うのと、感染率(β)の扱いが微妙に異なるのですが、式は日本語版に合わせてあります。
各種用語については、
に詳しく書いてあります。
元の SEIR モデルの場合、長期間(100年とか?)のシミュレーションになるので、出生率/死亡率 m があるのですが、新型コロナウィルスのシミュレーションをする場合は、短期間になるので m = 0 と仮定します。
function seir_eq(v,t,beta,lp,ip) {
b = beta
ds = -b*v[0]*v[2] // dS/dt = -βSI
de = b*v[0]*v[2]-(1/lp)*v[1] // dE/dt = βSI-E/lp
di = (1/lp)*v[1]-(1/ip)*v[2] // dI/dt = E/lp - I/ip
dr = (1/ip)*v[2] // dR/dt = I/ip
return [ds,de,di,dr];
}
Javascript のコードで肝になるのは、seir_eq 関数の部分です。
v が配列になっていますが、これが S,E,R,Iにあたります。
- v[0]:S Susceptible
- v[1]:E Exposed
- v[2]:I Infected
- v[3]:R Recovered
- beta: 感染率
- lp: 潜伏期間
- ip: 発病期間
それぞれのデルタ(差分)を加算していき、S,E,I,Rを計算します。
- R0: 基本生産数
感染率 beta は全体の初期の総数に関係するので、実際は、基本生産数 R0 を決めて beta を計算しています。
- 感染率(beta) = 感染者数(I) * 基本生産数(R0) / 無免疫数(S)
実際のところは、感染率は一定ではありません。閉鎖/開架空間、密集度、年齢などの違いにより、確率的に分散した値を持ち、また時間経過によって感染率下げる(感染者の隔離や治療など)ことがなされます。
また、SEIR モデルでは、状態遷移が必ず
- 無免疫 → 潜伏期間 → 発症 → 有免疫
の順になり、発症が伝播するというモデルになっています。
このあたりは、Javascript のコードを独自に変更する(潜伏期間にも発症するとか)もできるでしょう。
実験
で、実際のところはともかくとして、実験をしてみましょう。
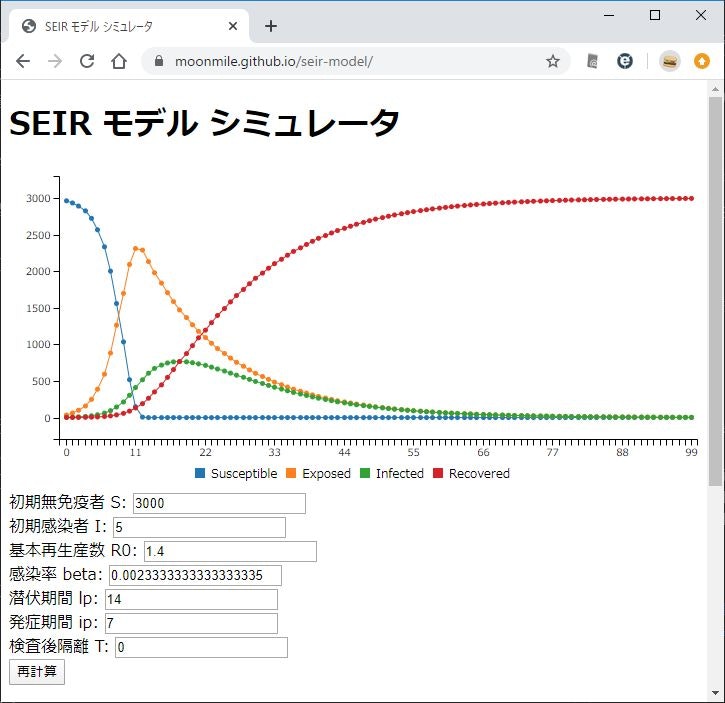
- 無免疫者 S: 3000
- 感染者 I: 5
- 基本生産数 R0: 1.4
- 潜伏期間: 14
- 発病期間: 7
漠然と閉鎖空間の場合は、発症者のピーク(緑色)が大きく出ます。
考えられる対策としては、
- 発症者のピークを後にずらす
- 発症者のピークを下げる
ことが考えられます。
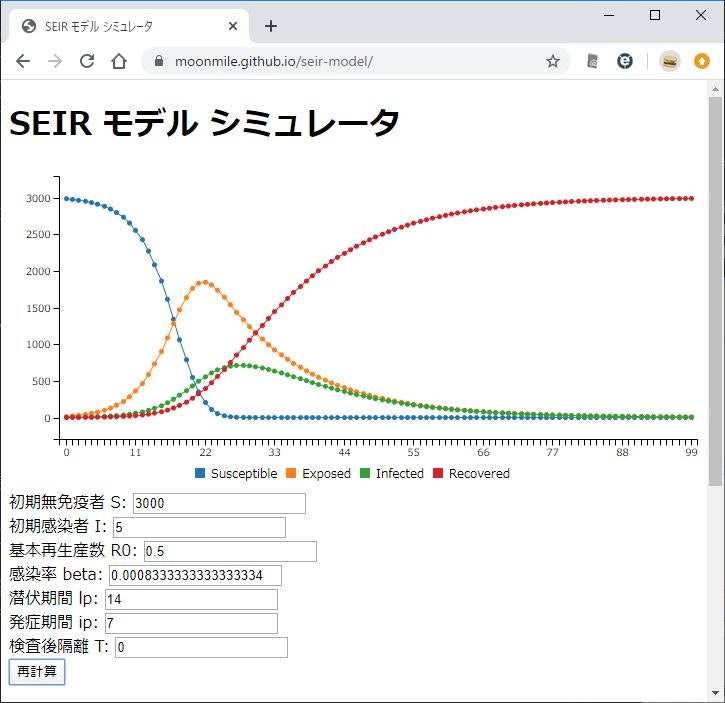
発症者のピークを後にずらすために、基本生産数 R0 を 0.5 ぐらいにさげてみましょう。
発症者のピークが後ろになるので、時間が稼げることがわかります。時間を稼ぐとワクチンの開発とか、インフルエンザのように暖かくなったから感染率が下がったとう現象が発生しそうです。
もうひとつは、発症者のピークを下げる方法です。
SEIR モデルでは、感染した感染したまま(苦笑)なのでそのまま拡大してしまいますが、普通は病院とかで治療しますよね。
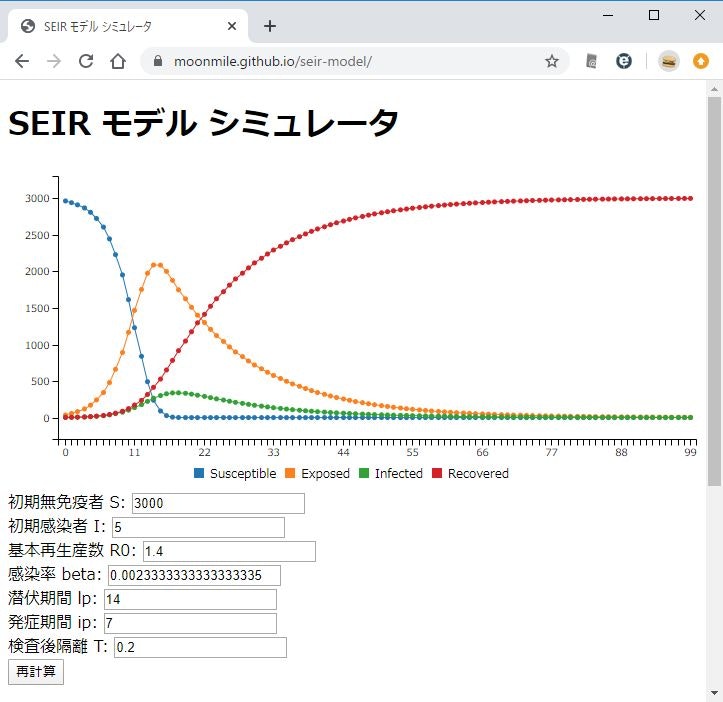
ここで検査後隔離(T) を入れてみましょう。
発症者のうち2割を隔離したときの状態を実験します。
// 感染者を発見して隔離する
dx = Ii * T
Ii = Ii - dx
Ri = Ri + dx // 免疫者に加算
コードの中では、感染者(I) から一定の隔離率(T) で、強制的に感染者から有免疫者に移行させます。
発病者のピークがぐっと下がっていることがわかります。
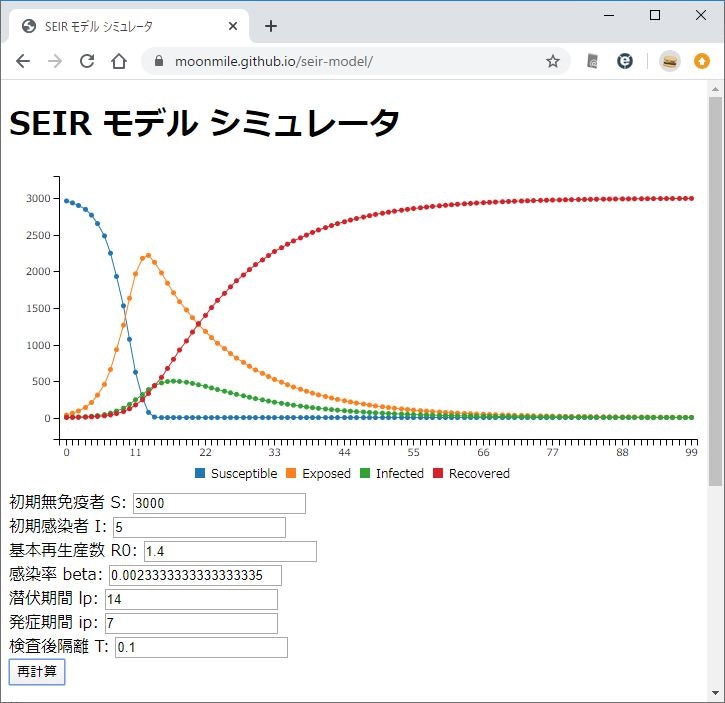
ちなみに、隔離率を0.1にしても、あまりピークは変わりません。
ただし、実際の隔離はPCR検査と偽陰性の割合が絡んでくるので、一律には決められません。
コード
コードは以下で公開しています。
moonmile/seir-model: SEIR model simulator
主要な javascript のコードはこんな感じです。
function seir_eq(v,t,beta,lp,ip) {
b = beta
ds = -b*v[0]*v[2] // dS/dt = -βSI
de = b*v[0]*v[2]-(1/lp)*v[1] // dE/dt = βSI-E/lp
di = (1/lp)*v[1]-(1/ip)*v[2] // dI/dt = E/lp - I/ip
dr = (1/ip)*v[2] // dR/dt = I/ip
return [ds,de,di,dr];
}
var Sinit = 3000 // 無免疫者(総数)
var Einit = 0 // 潜伏期間
var Iinit = 5 // 発病者
var Rinit = 0 // 有免疫
var R0 = 1.4 // 基本再生産数
var beta = Iinit * R0 / Sinit // 感染率 = (初期感染者*R0)/総数
var lp = 14 // 潜伏期間
var ip = 7 // 発症期間
var T = 0.0 // 検査で隔離
var lst = [] ;
function calc() {
var t_max = 100 ;
var dt = 1 ;
var state=[Sinit,Einit,Iinit,Rinit]
lst = []
console.log( state );
for ( var i=0; i<t_max; i++ ) {
var d = seir_eq( state, i, beta, lp, ip )
var Si = state[0]+d[0]
var Ei = state[1]+d[1]
var Ii = state[2]+d[2]
var Ri = state[3]+d[3]
// 感染者を発見して隔離する
dx = Ii * T
Ii = Ii - dx
Ri = Ri + dx // 免疫者に加算
// マイナス値を調節する
if ( Si < 0 ) {
Ei = Ei + Si; Si = 0;
}
if ( Ei < 0 ) {
Ii = Ii + Ei; Ei = 0;
}
if ( Ii < 0 ) {
Ri = Ri + Ii; Ii = 0;
}
state = [ Si, Ei, Ii, Ri ]
// console.log( state );
lst.push( state );
}
}
考察
あくまで SEIR モデルのシミュレーションしかないので、現実と一致するわけではありません。しかし、思考実験として先行きの状態を予測/想像するのは使えるのかなと思います。
いくつか現実にあわせるとすると、以下の条件が考えられます。
- 潜伏期間中の感染が予想されているので、潜伏(E) → 発症(I) の遷移が必要だろう
- 感染率の分散が大きい(空気感染ではなく、閉鎖空間での感染率が高いと思われる)ので、感染率/基本生産数を分散させる仕組みを入れる必要がある。
- 「クラスター対策」にあるように、あるクラスターから別のクラスターの伝播率を考慮する式を入れる。クラスター単位で SEIR モデルを作って、相互に伝播率を加えればよいか。