初めに
私は感染症の専門家ではありませんので、理解した上で読んでください。
2019年12月から中国湖北省武漢で発生した新型コロナ肺炎(Covid-19)が、日本にも広がり感染者数が増加しています。今後日本の感染者数がどう増えていくのか、興味があります。そのため感染予測モデルについて、論文を検索しました。
すでに世界中から感染モデルが発表されていますが、感染モデルで予測するときに精度に大きく影響するのが、感染率や隔離率などのパラメータです。これらのパラメータが実際の数値と異なると、実情とかけ離れた予測となってしまいます。
先日、中国の研究者からコロナウィルスの感染者数の予測モデルが発表されていました。
COVID-19 in Japan: What could happen in the future?
この論文では、予測モデルを中国の各地(武漢、北京、上海・・・)に適用して感染者数を精度良く予測できること、さらに日本に適用して今後感染者数が増加することを予測しています。またこの論文では、予測に必要なパラメータである感染率や隔離率が発表されていました(実際の感染者数に合うように調整したパラメータと言ったほうが正しいと思いますが)。
予測モデル
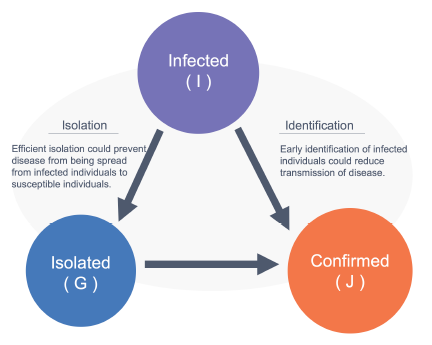
感染症モデルで使用されるのはSIRモデルやSEIRモデルですが、この論文ではちょっと異なるモデルを使用しています。statistical time delay dynamic model と呼んでいます。
[引用 COVID-19 in Japan: What could happen in the future?]
計算式は、以下のようになっています。
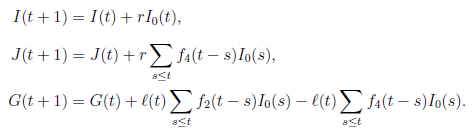
t : 日
I(t) : 累積感染者数
J(t) : 累積感染者数(病院で発症確定)
G(t) : その時に発生した感染者(累積値ではなく、発症確定していない)
I0(t) : 潜在感染者数(感染されているが感染確定も隔離もされていない)
I0(t) = I(t) − J(t) − G(t)
[引用 COVID-19 in Japan: What could happen in the future?]
パラメータ
このモデルを使用するうえで重要なパラメータと、発症率、入院率があります。
パラメータはこの論文に中国の例が記載されていました。
| 地域 | 成長率 | 感染率l1 | 感染率l2 | tl |
|---|---|---|---|---|
| 上海 | 0.3137 | 0.1713 | 0.6149 | 2020/1/16 |
| 北京 | 0.3125 | 0.1824 | 0.5880 | 2020/1/17 |
| 武漢 | 0.3019 | 0.1142 | 0.4567 | 2020/1/17 |
r 成長率
成長率は、一人の人がほかの人に感染させる割合です。
これは論文中の中国での数値をベースにして以下のように設定しました。
r = 0.3
l 隔離率
隔離率は、感染者が隔離される割合です。
これは論文中の中国での数値をベースにして以下のように設定しました。
l = 0.1(2020/2/28まで)
l = 0.5(2020/2/29から)
発症率
f2(t) 感染から発症への推移確率
これは論文には記載されていませんでした。
感染しても発症しない人が7-8割はいるというニュースを聞いています。
また発症するまでに長くても14日ということから、以下のように設定しました。
f2(t) = 0.2/14 × t (t < 14)
f2(t) = 0.2 (t >= 14)
入院率
f4(t) 感染から入院への推移確率
感染して入院した割合は、まったく分かりません。
そのため発症した人のうち、1/4が入院すると仮定して、以下のように設定しました。
f4(t) = 0.05/14 × t (t < 14)
f4(t) = 0.05 (t >= 14)
プログラム
from __future__ import print_function
import numpy as np
import pandas as pd
default_output = 'predict.csv'
class Corona():
def __init__(self, max_day):
self.r = 0.3 # 成長率
self.tl = 15 # 隔離開始日
self.l1 = 0.1 # 隔離開始日以前の隔離率
self.l2 = 0.5 # 隔離開始日以降の隔離率
self.i = np.zeros(max_day + 1)
self.i0 = np.zeros(max_day + 1)
self.j = np.zeros(max_day + 1)
self.g = np.zeros(max_day + 1)
def set_start(self):
# self.j[0] = 11 # 2020/1/30
self.j[0] = 21 # 2020/2/14
self.i[0] = self.j[0] * 10
self.g[0] = 0
self.i0[0] = self.func_i0(0)
def f2(self, t):
# 発症率
if t < 14:
a = 0.2/14.0
b = 0.0
y = a * t + b
else:
y = 0.2
return y
def f4(self, t):
# 入院率
if t < 14:
a = 0.05/14.0
b = 0.0
y = a * t + b
else:
y = 0.05
return y
def func_l(self, t):
# 隔離率
if t < self.tl:
return self.l1
else:
return self.l2
def func_i(self, t):
# 累積感染者数
# I(t + 1) = I(t) + r I0(t),
new_i = self.i[t] + self.r * self.i0[t]
return new_i
def func_j(self, t):
# 累積感染者数(病院で確定)
# J(t + 1) = J(t) + r Σs<t f4(t - s) I0(s)
sum1 = 0
for s in range(t):
sum1 += self.f4(t - s) * self.i0[s]
new_j = self.j[t] + self.r * sum1
return new_j
def func_g(self, t):
# 瞬間的に発生した感染者(病院で感染確認されていない)
# G(t + 1) = G(t) + f2(t) Σs<t f2(t - s) I0(s) - Σs<t f4(t - s) I0(s).
sum1 = 0
sum2 = 0
for s in range(t):
sum1 += self.f2(t - s) * self.i0[s]
for s in range(t):
sum2 += self.f4(t - s) * self.i0[s]
new_g = self.g[t] + self.func_l(t) * sum1 - self.func_l(t) * sum2
return new_g
def func_i0(self, t):
# 潜在感染者数(感染されているが感染確定も隔離もされていない)
# I0(t) := I(t) - J(t) - G(t)
new_i0 = self.i[t] - self.j[t] - self.g[t]
if new_i0 < 0.0:
new_i0 = 0.0
return new_i0
def predict(self, day):
# 初期化
period = day + 1
predict_data = np.zeros([period, 5])
df_predict = pd.DataFrame(predict_data, columns=['day', 'I', 'J', 'G', 'I0'])
self.set_start()
# 予測
for i in range(period - 1):
self.i[i+1] = self.func_i(i)
self.j[i+1] = self.func_j(i)
self.g[i+1] = self.func_g(i)
self.i0[i+1] = self.func_i0(i)
df_predict.loc[i, 'day'] = i+1
df_predict.loc[i, 'I'] = self.i[i+1]
df_predict.loc[i, 'J'] = self.j[i+1]
df_predict.loc[i, 'G'] = self.g[i+1]
df_predict.loc[i, 'I0'] = self.i0[i+1]
return df_predict
def main():
corona = Corona(25)
predict = corona.predict(25)
predict.to_csv(default_output, index=False)
if __name__ == "__main__":
main()
結果
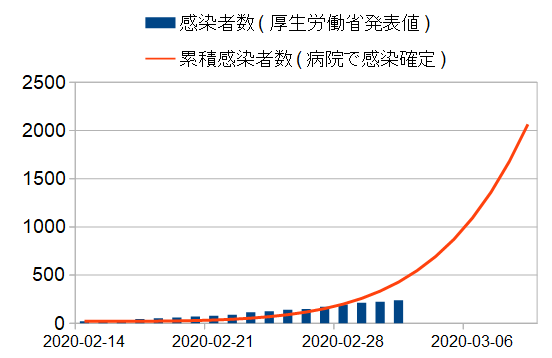
感染者数(病院で感染が確認された方)
厚生労働省報道発表資料で毎日発表される資料から、シミュレーション開始時点の感染者数を入手しました。
2020/2/14の感染者21名をベースにして、2/15から予測しました。
予測結果は以下の通りです。
| 日付 | 感染者数(厚生労働省発表) | 感染者数(予測) |
|---|---|---|
| 2020/2/14 | 21 | 21 |
| 2020/2/15 | 21 | 21 |
| 2020/2/16 | 21 | 21 |
| 2020/2/17 | 46 | 22 |
| 2020/2/18 | 53 | 23 |
| 2020/2/19 | 60 | 25 |
| 2020/2/20 | 70 | 29 |
| 2020/2/21 | 79 | 35 |
| 2020/2/22 | 90 | 43 |
| 2020/2/23 | 114 | 54 |
| 2020/2/24 | 126 | 69 |
| 2020/2/25 | 140 | 90 |
| 2020/2/26 | 149 | 118 |
| 2020/2/27 | 171 | 153 |
| 2020/2/28 | 195 | 200 |
途中は誤差が大きいですが、2/28では誤差がわずか5名でした。
(たまたまかもしれませんが・・・・)
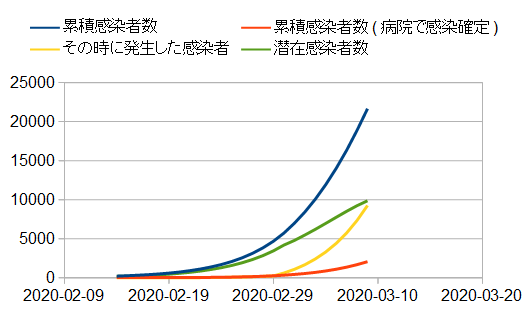
潜在感染者数(病院で感染が確認されていない方)
上記の感染者数は、病院で感染確定された人だけです。
シミュレーションでは、潜在感染者数も計算されています。その結果が以下の図です。
オレンジ色:病院で感染が確定された人(累積)
紺色 :病院で感染が確定されていない、隠れた感染者(累積)
隠れた感染者は、病院で感染が確定された人よりはるかに多く、10倍くらいいるのですね。
感想
厚生労働省の方もこのようなシミュレーションを行っているのでしょうか?
参考文献
2020/3/3変更
プログラム修正
本投稿のプログラムを使用して、他の方がHatena Blogを書かれていました。
https://kibashiri.hatenablog.com/entry/2020/03/02/171223
この方のブログに、プログラムの間違いの指摘がありました。
確かにfunc_g()の計算の符号間違いでした。
プログラムと結果を修正しました。
予測結果
予測では、2/29以降の感染者は毎日100人近く増加する予想になっています。厚生労働省から新しい感染者数(国内事例-チャーター便帰国者を除く)が発表されたので、予測結果と比較してみました。
| 日付 | 感染者数(厚生労働省発表) | 感染者数(予測) | PCR検査人数(1日での) |
|---|---|---|---|
| 2020/2/29 | 215 | 259 | 130 |
| 2020/3/1 | 224 | 334 | 178 |
| 2020/3/2 | 239 | 428 | 96 |
| 2020/3/3 | 253 | 546 | 71 |
予測値は実際の感染者数と大きくずれ、2/29以降の予測性能は良くなかったようです。中国と同じパラメータで日本の感染者数が予測できるか試したのですが、日本と中国では事情が異なり、同じパラメータでの予測には限界があることが分かりました。
報道では日本のPCR検査能力は3800名/日と報道されていましたが、実際の1日の検査人数は130人、178人、96人、71人と予想外に少ないのですね。