はじめに
Goの正規表現は遅いと言われていることが以前から疑問だったので調査してみました。
- ① 現実的なユースケース(例えばURLのパースなど)ではGo言語の正規表現は使うべきではなく、
stringsパッケージの標準の関数を利用した方がパフォーマンスとしては良い。 - ② Go言語で正規表現を利用するために必要な"正規表現オブジェクト"を並行にアクセスするにはパフォーマンスが問題になるので注意が必要。
とあります。その理由は、それぞれ以下に集約できるようです。
- ① Go言語標準の正規表現ライブラリは、正規表現と検査文字列の長さに対して常に$O(n^2)$のオーダーで計算量が増加する安定したアルゴリズムを採用している。
- ② "正規表現オブジェクト"を用いたマッチング処理には排他制御が行われている。
調べてみる
Go言語のpkg/regexpの公式ドキュメントページを見にいくとGoのリードメンテナのRuss Cox氏のRegular Expression Matching Can Be Simple And Fastという記事(本記事で以降何度も参照します)に詳細が載っていました。
① 安定したアルゴリズムとは?
Ken Thompson1が1968年に論文で発表したThompson NFAアプローチという正規表現の実装手法をほぼそのままGo言語の標準パッケージとして採用したようです。
上記のRuss Cox氏の記事では入力文字 $a^n$ に対する正規表現 $a?^na^n$ のケース2でパフォーマンス評価を行っています。
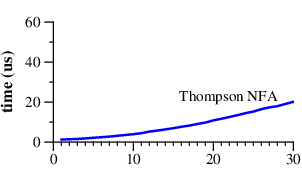
PerlやRubyなどの言語で採用されている正規表現エンジンでは**(あくまでもこのケースでは)**指数関数的にコストがかかるのに対し、Thompson NFAアプローチならば"理論的には"線形に増加していくとのことです。
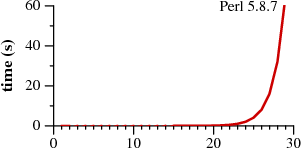
著者もTypoじゃないよ、と前置きしているようにPerlの場合、$n$がある部分を堺に処理時間が急激に増加することが下記画像でわかります。
※ 横軸は$n$
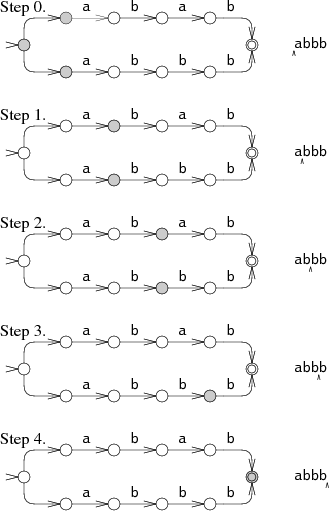
Thompson NFAアプローチでは始めに対象の正現表現から非決定性有限オートマトン(NFA)を生成します。3
Goの実装ではregOjb := regexp.MustCompile("a?a?a?aaa")と正規表現をコンパイルすることでregOjbには*regexp.Regexp型の値としてNFAを表した構造体へと変換されます。4
生成されたNFAモデルを元に入力文字列をマッチ処理をする際、下記図のように各分岐ルートを"並列に独立"して処理されるならば最悪ケースでも文字数に対して線形時間で処理できることがThompson NFAアプローチでは保証されます。
② なぜ排他制御が必要なのか?
Go言語の正規表現が遅いと言われる理由の一つに、マッチ処理にて排他制御を実施しているためと指摘されていますが、なぜ排他制御を実施するのでしょう?
それもThompson NFAアルゴリズムが理由のようです。
記事での説明によると、Thompson NFAアルゴリズムはマッチング処理の際、辿るステップに応じた決定性有限オートマトン(DFA)を計算することになります。
この計算結果により生成されたDFAを次の機会にも利用できるように、Goの実装ではDFAをキャッシュします。
そのキャッシュの処理時に排他制御が必要になるということです。
実装を見ると以下の箇所にてmatchPoolという専用のメモリ領域でキャッシュ戦略をしていることがわかります。
// doExecute finds the leftmost match in the input, appends the position
// of its subexpressions to dstCap and returns dstCap.
//
// nil is returned if no matches are found and non-nil if matches are found.
func (re *Regexp) doExecute(r io.ByteReader, b []byte, s string, pos int, ncap int, dstCap []int) []int {
// 中略
m := re.get() // キャッシュがあれば利用。なければ新しいDFAを生成。
i, _ := m.inputs.init(r, b, s)
m.init(ncap)
if !m.match(i, pos) {
re.put(m) // DFAのキャッシュを保存 ← このとき排他制御を実施
return nil
}
dstCap = append(dstCap, m.matchcap...)
re.put(m) // DFAのキャッシュを保存 ← このとき排他制御を実施
return dstCap
PoolにDFAを入れ込む箇所にて以下のように排他制御がかかっていることがわかります。
// Put adds x to the pool.
func (p *Pool) Put(x interface{}) {
if x == nil {
return
}
if race.Enabled {
if fastrand()%4 == 0 {
// Randomly drop x on floor.
return
}
race.ReleaseMerge(poolRaceAddr(x))
race.Disable()
}
// (後略)
計測してみる
上記記事でのケース(入力文字 $a^n$ に対する正規表現 $a?^na^n$)にてGoの標準正規表現エンジンとPerlのものでどのように差が出るか実際に計測してみます。
実行環境
- Macbook Pro 13-inch, 2017
- macOS Mojave version 10.14.6
- プロセッサ 2.3GHz Intel Core i5
- Go
- go version go1.12.5 darwin/amd64
- Perl
- perl 5, version 18, subversion 4 (v5.18.4) built for darwin-thread-multi-2level
Goの場合
package main
import (
"fmt"
"regexp"
"time"
)
func main() {
for _, n := range []int{1, 10, 100, 1000, 10000} {
// Generate target string
var s1 string
for i := 0; i < n; i++ {
s1 += "a?"
}
var s2 string
for i := 0; i < n; i++ {
s2 += "a"
}
re := s1 + s2 // a?a?a?aaa (ex. n==3)
fmt.Println("n:", n)
start := time.Now()
// Compile to NFA
regOjb := regexp.MustCompile(re)
// Do matching
regOjb.MatchString(s2)
end := time.Now()
fmt.Printf("%f [sec]\n", (end.Sub(start)).Seconds())
}
}
n: 1
0.000094 [sec]
n: 10
0.000053 [sec]
n: 100
0.000237 [sec]
n: 1000
0.050289 [sec]
n: 10000
3.086724 [sec]
上記の結果から$n$が10倍になる度に処理時間がおおよそ100倍分になっているので、二次関数のオーダー$O(n^2)$ということがわかります。
この観測結果は上記記事の中でもPerformanceの節にて言及されており、正規表現の長さが$m$で入力文字列の長さが$n$のとき、実際には$O(mn)$のオーダーになると記述されています。
Thompson's algorithm maintains state lists of length approximately n and processes the string, also of length n, for a total of O(n2) time. (The run time is superlinear, because we are not keeping the regular expression constant as the input grows. For a regular expression of length m run on text of length n, the Thompson NFA requires O(mn) time.)
実装を見ると、この部分からだいたいを読み取れるように、NFA構造上でマッチング処理が走る際、並行で走る複数スレッド分(正規表現の長さm分)に対してのfor文(step関数内のfor文)が、ステップ分(入力文字列の長さn分)に対してのfor文(match関数内のfor文)内で走っているため$O(mn)$のオーダーであると推測できます。
Perlの場合
上記のGoと同じ内容のプログラムをPerlで作って動かしてみます。
use Time::HiRes qw( gettimeofday tv_interval );
my @ns = (1, 10, 25, 26, 27, 28, 29, 30);
foreach my $n (@ns) {
my $s1 = "";
for (my $i = 0; $i < $n; $i++) {
$s1 = $s1 . "a?";
}
my $s2 = "";
for (my $i = 0; $i < $n; $i++) {
$s2 = $s2 . "a";
}
my $re = $s1 . $s2; # a?a?a?aaa (ex. n==3)
my $t0 = [gettimeofday];
# Do matching
$s2 =~ /$re/;
my $elapsed = tv_interval($t0);
print "n: $n\n";
print "$elapsed [sec]\n";
}
n: 1
1.4e-05 [sec]
n: 10
8.7e-05 [sec]
n: 25
1.31766 [sec]
n: 26
2.631269 [sec]
n: 27
5.284664 [sec]
n: 28
10.651156 [sec]
n: 29
20.998345 [sec]
n: 30
42.14693 [sec]
上記の結果から、$n$が1増えるごとに処理時間が2倍に増加しているので$O(2^n)$の指数関数のオーダーであることが確認できました。
記事の下記箇所にもあるようにPerlやRubyなどで実装されている手法(Backtracking)では正規表現$a?^na^n$にて$2^n$個の全パターンを網羅するよう処理してしまうためこの結果になるとわかります。
Backtracking regular expression implementations implement the zero-or-one ? by first trying one and then zero. There are n such choices to make, a total of 2n possibilities. Only the very last possibility—choosing zero for all the ?—will lead to a match. The backtracking approach thus requires O(2n) time, so it will not scale much beyond n=25.
GoとPerlの結果から記事における下記図の計測結果を再現することができました。(※グラフの縦軸は対数をとっています。)
感想
Go言語における正規表現パフォーマンスの特徴はGo言語の設計自体に依るものではなく、正規表現におけるGoの標準パッケージ上の実装がThompson NFAというモデルを採用したことに由来するとわかりました。
Goの正規表現は使うべきではないと頭ごなしに決めつけずに、ケースに応じて検証するべきでしょう。
追記
2019年8月14日記載
コメント欄にてご指摘いただいたように、本記事では包括的に正規表現エンジンを扱えていないのにGo以外がすべて同じであるかのような言い方をしていたので修正しました。
また、本記事(Russ Cox氏の記事)の比較は正規表現 $a?^na^n$ というPerlやRuby等の正規表現エンジンでの方法(Backtracking)では苦手とする特殊なケースであるのでそういったケースであることを明示するように修正しました。
参考
- https://swtch.com/~rsc/regexp/regexp1.html
- https://medium.com/veltra-engineering/how-slow-is-golangs-regular-expression-9d210ceb70b0
- https://medium.com/eureka-engineering/regexpとの付き合い方-go言語標準の正規表現ライブラリのパフォーマンスとアルゴリズム-984b6cbeeb2b
-
UNIXのオリジナル開発者の1人。Go初期のコントリビューター。CS分野の数々の功績を持つ。 ↩
-
$n$ が3の場合、入力文字は $aaa$ で正規表現は $a?a?a?aaa$ です。 ↩
-
正規表現ならばNFAに変換可能($\Rightarrow$は真)、その逆も可能($\Leftarrow$も真)です。その証明に関しては計算理論の基礎 [原著第2版] 1.オートマトンと言語の書籍に詳細が載っています。 ↩
-
この処理はコストがかかるので、Goのユーザは基本的にプロセス起動の初期化時のみに生成するよう実装するべきです。 ↩