はじめに
Fubiniの定理の流れがわかったのでチャート図でまとめておく。
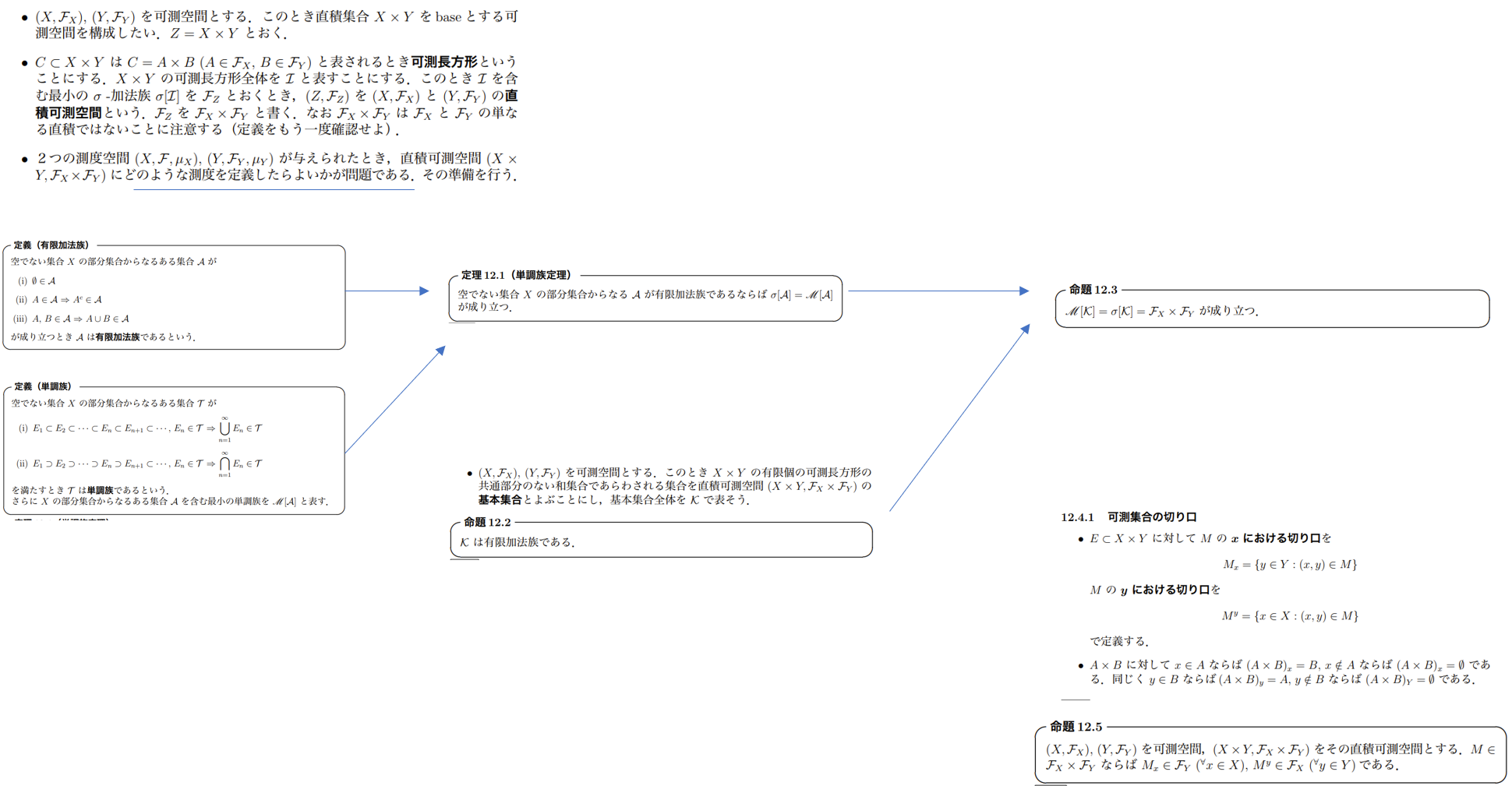
単調族定理
ポイント!
有限加法族を含む単調族は$\sigma$-加法族となる。
直積可測空間について
基本集合の全体$\mathcal{K}$が有限加法族となり、基本集合の全体$\mathcal{K}$を含む単調族は$\mathcal{F}_X\times\mathcal{F}_Y$に一致する。
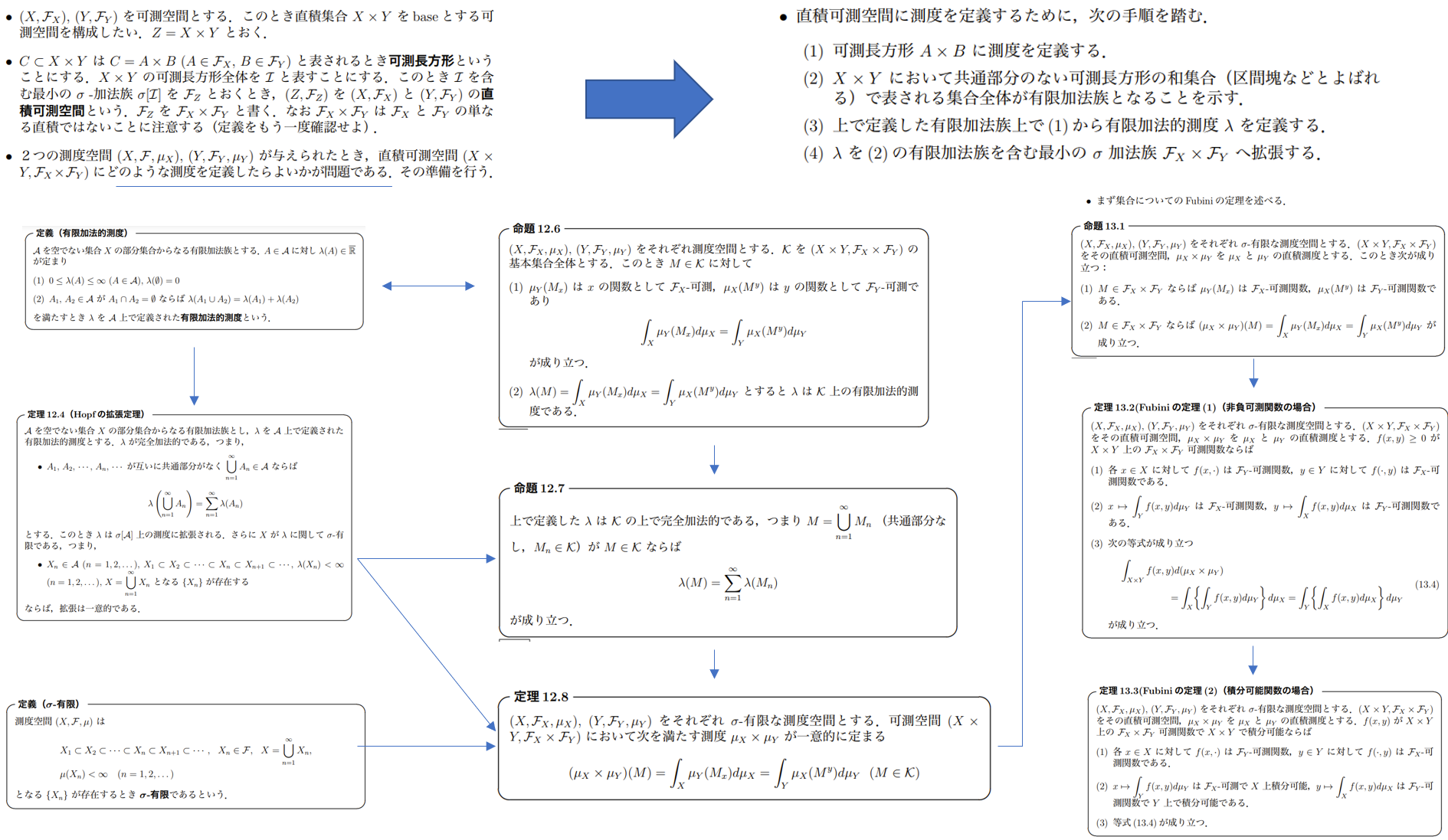
E.Hopsの拡張定理とFubiniの定理
ポイント!
有限加法的測度に完全加法性を仮定すれば、有限加法的測度は完全加法的に拡張される。さらに、$\sigma$-有限と仮定すれば、拡張された有限加法的測度はE.Hopfの拡張定理より一意的に定まる。
直積測度について
基本集合$M$の$x$における切り口$M_x$と、基本集合$M$の$y$における切り口$M^y$のルベーグ積分が一致する。その基本集合$M$の測度$\lambda(M)$と一致すると仮定すると、その測度は有限加法的測度といえる。さらに、完全加法的である。ここで、$\mu_Y$と$\mu_Y$ともに$\sigma$-有限であると仮定すると、直積測度$\mu_X\times\mu_Y$を
$$
\mu_X\times\mu_Y(M_n):=\lambda(M_n)=\mu_X(X_n)\mu_Y(Y_n)
$$
とおけば、直積測度$\mu_X\times\mu_Y$は$\sigma$-有限であるので、E.Hopfの拡張定理から直積測度$\mu_X\times\mu_Y$は一意的に定まる。
Fubiniの定理について
Fubiniの定理を集合、非負可測関数(特性関数、単関数、可測関数)、積分可能関数の順に拡張して証明していけばよい。