はじめに
ChatGPTが普及し、世間も落ち着いてきました。ChatGPTを使ってみて凄いなと思いましたが、どんな仕組みなんだろう?と不思議に思いました。ChatGPTの元ネタとウワサされているInstruct GPTの仕組みに興味が湧いたので、調査してみました。
この記事は、@omiita(オミータ)さんの記事を参考にしました。
Instruct GPTの学習
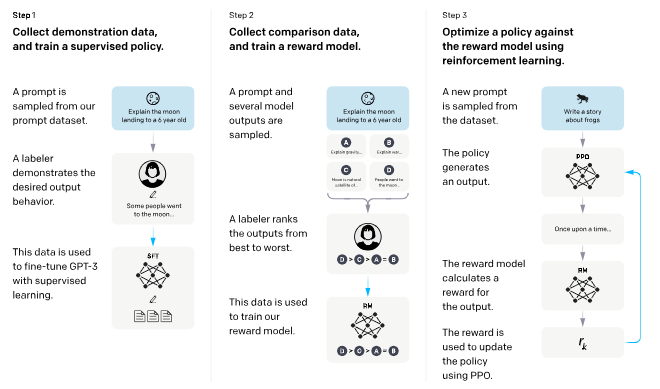
Instruct GPTの論文では3ステップでモデルを学習させています。
-
Step1では、1プロンプトに対して、labelerが望ましい出力を与え、SFT(GPT-3)をファインチューニングする。
-
Step2では、1プロンプトに対して、様々なモデルが出力し、labelerがアウトプットに対して選好を決める。そのデータを用いて、報酬関数reward modelを学習する。
-
step3では、新しい1プロンプトをサンプリングし、強化学習PPOの方策policyが出力を生成する。出力に対して、報酬関数reward modelが報酬を計算する。報酬関数reward modelを用いて、方策policyを学習する。
SFTはGPT-3みたいなものと考えればとりあえずよさそうです。
しかし、これだけでは、報酬関数reward modelと方策policyをどのように学習させているか不透明です。
詳しくみていきましょう。
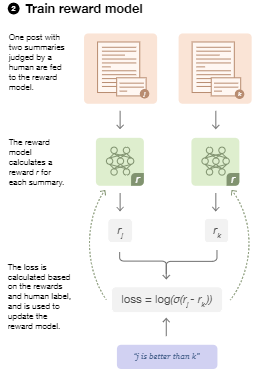
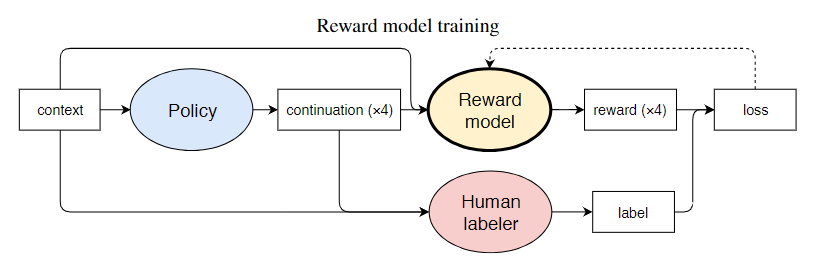
reward modelの学習
コマンド$x$を与えたとき、出力$y\in\lbrace y_0,y_1\rbrace$のどちらがいいかlabelerが判断します。仮に、ラベル$i$が望ましい場合のreward modelの損失lossは以下の通りです。
\mathrm{loss}(\theta)=-\mathbb{E}_{(x,y_0,y_1,i)\sim D}[\log(\sigma(r_{\theta}(x,y_i)-r_{\theta}(x,y_{1-i})))]
ここで、$\sigma$はシグモイド関数です。
イメージをつけるために、例えを出します。
ラベル$i$のほうが望ましいと報酬$r_\theta$が算出すれば、$r_{\theta}(x,y_i)-r_{\theta}(x,y_{1-i})>0$となり、損失lossが小さくなります。一方で、ラベル$i$のほうが望ましくないと報酬$r_\theta$が算出すれば、$r_{\theta}(x,y_i)-r_{\theta}(x,y_{1-i})<0$となり、損失lossが大きくなります。
この損失lossが最小となるように、reward modelを学習させます。
上記の損失lossは2個ずつサンプリングしたときの結果ですが、Instruct GPTでは$K$個のデータをセットでサンプリングしたときの損失lossを計算します。$y_w$の方が$y_l$より好ましいものとします。
\mathrm{loss}(\theta)=-\dfrac{1}{_KC_2}\mathbb{E}_{(x,y_w,y_l)\sim D}[\log(\sigma(r_{\theta}(x,y_w)-r_{\theta}(x,y_{l})))]
この損失lossが最小となるように、reward modelを学習させます。
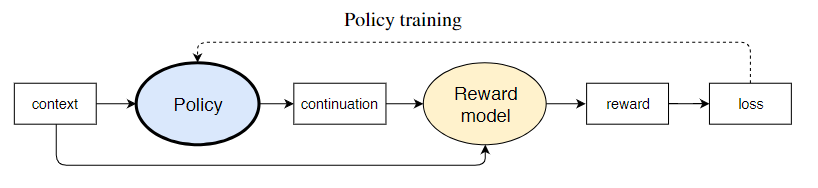
policyの学習
報酬$R$は、強化学習PPOのpolicy $\pi_{\phi}^{RL}$が、SFTの方策$\pi^{SFT}$から大きく離れないように、KLダイバージェンスの項を追加したものとします。
R(x,y) = r_{\theta}(x,y)-\beta \log\left[\dfrac{\pi_{\phi}^{RL}(y|x)}{\pi^{SFT}(y|x)}\right]
目的関数objectiveである報酬の期待値が最大となるように、policy $\pi_{\phi}^{RL}$を学習させます。
ただし、pretrain datasetはモデルを事前に学習させるのに用意していたデータセットで、ここから大きく変わった結果がでないようにする項をいれています。
\mathrm{objective(\phi)}=
\mathbb{E}_{(x,y)\sim D_{\pi_{\phi}^{RL}}}
\left[
r_{\theta}(x,y)-\beta \log\left(\dfrac{\pi_{\phi}^{RL}(y|x)}{\pi^{SFT}(y|x)}\right)\right]
+\gamma \mathbb{E}_{x\sim D_{\mathrm{pretrain}} }\left[\log \left(\pi_{\phi}^{RL}(x)\right)\right]
おわりに
ソースコードを公開した方がいるので、リバースエンジニアリングをしてみようと思います。