普通のPyTorchやTensorFlowで正規分布以外の連続値の分布を予測する

はじめに

先日、muzero-generalの実装を見ていたときに、連続値の予測としてcategoricalに予測する面白い方法がありました。

よくよく考えてみると、連続値の任意の確率分布の予測を表現できるんじゃないかな、と思って検証してみたら、上手く行きそうだったのでメモしておきます。

連続値をcategoricalに予測する

連続値の予測に MeanSquaredError を使うと基本的に「予測したい値の分布が正規分布である（さらに、関心があるのは期待値だけである）」という前提があることになります。なので例えば、山が2つあるような分布だと、その間くらいを予測してしまってちょっと都合が悪かったりします。広がり具合（分散など）もちょっとわかりません。
（関心のある）値の範囲は決まっている場合、次のような方法があります。

例えば、値の範囲が 0 ~ 10 だとすると、v=[0, 1, 2, ..., 10] という 11の値の点を決めます。
最初に p[0~10] = 0 として、
例えば 3.7 という値なら p[3] = 0.3, p[4]=0.7 と表現します。0.1なら p[0]=0.9, p[1]=0.1 です。3 なら p[3]=1.0 です。要するに、値の両端に対して所属度合いを振っていく感じです。

逆に、この p から元の値を計算する場合は、期待値 sum(p*v) を計算します。

コードで書くとこんな感じになります。

import numpy as np

SUPPORT_SIZE = 11
VALUE_RANGE = [0., 10.]


def scalar_to_support(scalars):
  values = np.array(scalars)
  min_v, max_v = VALUE_RANGE
  values = np.clip((values - min_v) / (max_v - min_v), 0., 1.)
  key_values = np.linspace(0., 1., SUPPORT_SIZE)

  r_index = np.searchsorted(key_values, values, side="left")  # a[i-1] < x <= a[i]
  l_index = np.clip(r_index-1, 0, len(key_values))
  left_vs = key_values[l_index]
  right_vs = key_values[r_index]

  interval = key_values[1] - key_values[0]
  left_ps = 1-(values - left_vs)/interval
  right_ps = 1-(right_vs - values)/interval

  vectors = np.zeros((len(values), SUPPORT_SIZE))
  for i in range(len(scalars)):
    vectors[i, l_index[i]] = left_ps[i]
    vectors[i, r_index[i]] = right_ps[i]

  return vectors

def support_to_scalar(supports):
  min_v, max_v = VALUE_RANGE
  key_values = np.linspace(min_v, max_v, SUPPORT_SIZE)
  supports /= supports.sum(axis=1, keepdims=True)
  return np.sum(supports * key_values, axis=1)

※ muzeroの実装では、更に前処理として面白い変換をしていますが、それは省いています。

学習させる場合は、出力は softmax(この場合は11要素) にして、Loss関数にはCrossEntropyを使います。

確率分布を学習できるのかの検証

覚えたてのPyTorchを使って検証してみます。

定数の予測

まずは、何か１つの値を固定で予測できるかやってみます。

コード

# on jupyter notebook
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt

SUPPORT_SIZE = 101


class Net(torch.nn.Module):
  def __init__(self):
    super().__init__()
    self.fc = torch.nn.Linear(1, SUPPORT_SIZE)

  def forward(self, x):
    x = self.fc(x)
    x = F.softmax(x, dim=1)
    return x


def get_dummy_input(batch_size):
    dummy_inputs = np.random.random((batch_size, 1)).astype("float32")
    return torch.tensor(dummy_inputs)  # dummy

def constant_target_value_fn(const):
  def fn(batch_size):
    return [const] * batch_size
  return fn

def train_model(model, target_value_fn, epoch=1000, lr=0.01, batch_size=16):
  optimizer = torch.optim.Adam(model.parameters(), lr=lr)

  loss_history = []
  for ep in range(epoch):
    target_values = target_value_fn(batch_size)
    target_supports = torch.tensor(scalar_to_support(target_values))
    #
    optimizer.zero_grad()
    outputs = model(get_dummy_input(batch_size))
    losses = torch.mean(- target_supports * torch.log(outputs))
    losses.backward()
    optimizer.step()
    loss_history.append(losses.item())

  plt.plot(loss_history)
  plt.show()

#######################

model = Net()
train_model(model, constant_target_value_fn(4.8))
outputs = model(get_dummy_input(5)).detach().numpy()
print(f"期待値={np.mean(support_to_scalar(outputs))}")

vs = np.mean(outputs, axis=0)
plt.plot(vs)

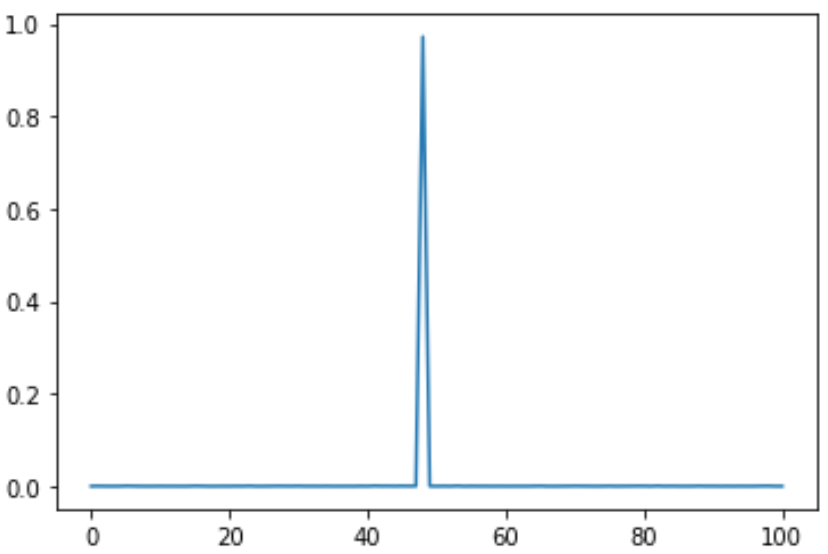
対象範囲を0~10、出力ベクトルのサイズを101にして、4.8 という定数を予測させてみました。
予測結果はこうなりました。問題なさそうです。

期待値=4.804064254500373

※ 横軸が0~100になってますが、0~10だと思ってください。以降も同じ。

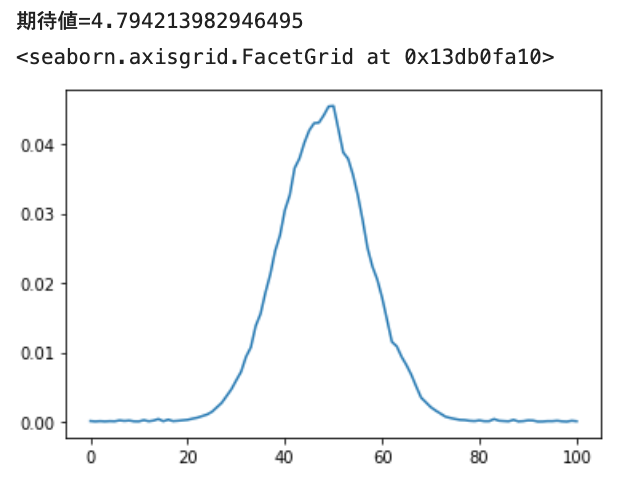
正規分布の予測

次に正規分布(loc=4.8, scale=0.9)を学習させてみます。

コード

from scipy import stats

def norm_fn(loc, scale):
  def fn(batch_size):
    dist = stats.norm(loc=loc, scale=scale)
    return dist.rvs(batch_size)
  return fn

model = Net()
distribution_fn = norm_fn(4.8, 0.9)
train_model(model, distribution_fn, epoch=1000, batch_size=1024)
outputs = model(get_dummy_input(5)).detach().numpy()
print(f"期待値={np.mean(support_to_scalar(outputs))}")

vs = np.mean(outputs, axis=0)
plt.plot(vs)

いい感じ。

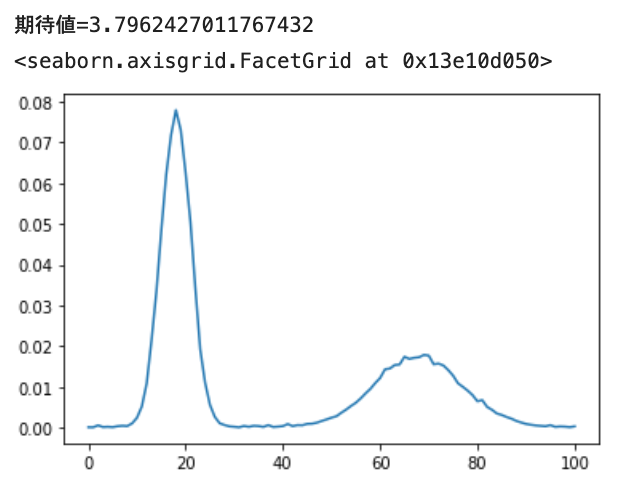
混合正規分布の予測

次に２つの正規分布 Normal(loc=1.8, scale=0.3, 確率=0.6) と Normal(loc=6.8, scale=0.9, 確率=0.4) を学習させてみます。

コード

from collections import Counter
def multi_norm_fn(loc_scale_prob_list):
  def fn(batch_size):
    values = []
    for loc, scale, prob in loc_scale_prob_list:
      dist = stats.norm(loc=loc, scale=scale)
      values.append(dist.rvs(batch_size))
    ps = np.array([p for _, _, p in loc_scale_prob_list])
    ps = ps / np.sum(ps)
    count = Counter(np.random.choice(range(len(values)), size=batch_size, p=ps))
    ret = []
    for i, cnt in count.items():
      ret += list(values[i][:cnt])
    return ret
  return fn


model = Net()
distribution_fn = multi_norm_fn([
  [1.8, 0.3, 0.6],
  [6.8, 0.9, 0.4],
])
train_model(model, distribution_fn, epoch=1000, batch_size=1024)
outputs = model(get_dummy_input(5)).detach().numpy()
print(f"期待値={np.mean(support_to_scalar(outputs))}")

vs = np.mean(outputs, axis=0)
plt.plot(vs)

おー、ちゃんと２山できますね。あと、裾野の広さも表現されています。

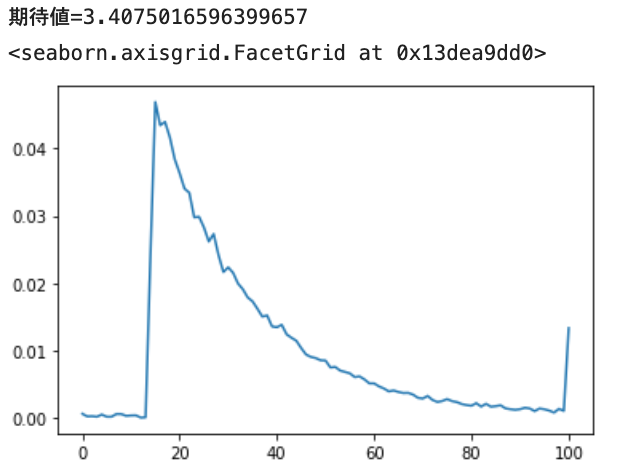
指数分布の予測

最後に指数分布(loc=1.4, scale=2.0)です。
※ 普通の指数分布(2)を1.4だけ右に平行移動したものになります。

コード

def exp_fn(loc, scale):
  def fn(batch_size):
    dist = stats.expon(loc, scale)
    return dist.rvs(batch_size)
  return fn

model = Net()
distribution_fn = exp_fn(1.4, 2.0)
train_model(model, distribution_fn, epoch=1000, batch_size=1024)
outputs = model(get_dummy_input(5)).detach().numpy()
print(f"期待値={np.mean(support_to_scalar(outputs))}")

vs = np.mean(outputs, axis=0)
plt.plot(vs)

1.4 辺りからピークが立ち上がり、徐々に落ちていくのが表現されています。また、10以上の値がそれなりにあることも表しています。

余談

あと、角度みたいに循環する連続値の予測にはかなりぴったりかな、と思います。
10度と350度は実は近いんだよ、というのがちょっと工夫すれば表現できそうです。

さいごに

ということで、連続値予測はCategoricalにCrossEntropyでもOK、というのが確認できました。
こういうテクニックは最近の書籍などを読むと載っているのかもしれませんが、個人的に新しかったのでメモしておきます。