浮動小数点数オタクが AtCoder Beginner Contest 169 のC問題をガチで解説してみる

どうも、浮動小数点数オタクのmod_poppoです。

昨日開催された ABC169 の C 問題が浮動小数点数の罠な問題だったらしいので、どこが罠なのか、そしてどうすれば罠を回避できるのかを解説してみます。

また、典型的な誤答に対しては、それを落とすためのテストケースも用意しました。

問題文（引用）

まず最初に問題文を引用しておきます。

• AtCoder Beginner Contest 169 | C - Multiplication 3

問題文

$A\times B$ の小数点以下を切り捨て、結果を整数として出力してください。

制約

• $0\le A\le 10^{15}$
• $0\le B<10$
• $A$ は整数
• $B$ は小数第 2 位まで与えられる

入力

入力は以下の形式で標準入力から与えられる。

A B

出力

答えを整数として出力せよ。

問題文はいたってシンプルですね。

誤答例1：浮動小数点数の精度

まずは素直に、A と B をそれぞれ倍精度浮動小数点数として読み込んで、浮動小数点数として掛け算してみます。

実装例

C++による実装：

#include <iostream>
#include <cstdint>
#include <cmath>

int main()
{
    double a, b;
    std::cin >> a >> b;
    std::cout << (std::int64_t)std::floor(a * b) << std::endl;
}

Pythonによる実装：

a, b = input().split()
a = float(a)
b = float(b)
print(int(a * b))

Haskellによる実装：

{-# LANGUAGE TypeApplications #-}
main = do
  [a,b] <- map (read @Double) . words <$> getLine
  print (truncate $ a * b :: Integer)

解説

倍精度浮動小数点数の精度は53ビットなので、 $2^{53}$ 以下の整数は正確に表現できます。$2^{53}$ はおよそ $9.01\times 10^{15}$ なので、入力の $A$ を読み込むことに支障はありません。

一方、計算結果 $A\times B$ を正確に表すためには、小数点以下の2桁も含めて、10進法で18桁を表現できる必要があります。

よって、 $A\times B$ を倍精度浮動小数点数（有効数字は16桁程度）として計算してしまうと精度が足りません。

テストケース

入力例：

999999999999900 9.25

正しい出力：

9249999999999075

積は正確に 9249999999999075 となります。

誤答例1の実行結果：

9249999999999076

入力の 999999999999900 も 9.25 も正確に倍精度浮動小数点数で表現できますが、積の 9249999999999075 は倍精度浮動小数点数では表現できないので、間違った答えが出力されます。

誤答例2：浮動小数点数の丸め

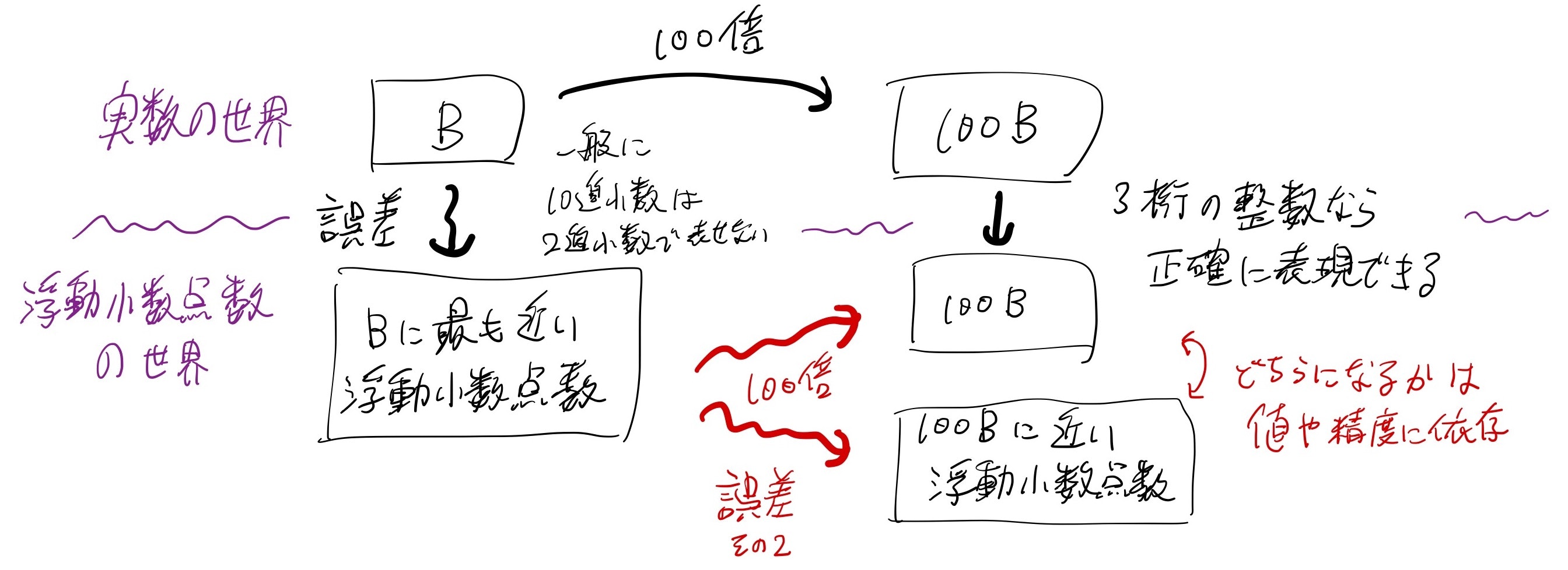
$A\times B$ を倍精度浮動小数点数で計算してしまうと精度が足りませんでした。しかし、最終的な答えは64ビット整数で表せるはずなので、積を64ビット整数で計算すれば精度が足りない問題を回避できそうです。そこで、今度は $B$ を100倍して整数にしてから乗算してみます。

実装例

C++による実装：

#include <iostream>
#include <cstdint>

int main()
{
    std::int64_t a;
    double b;
    std::cin >> a >> b;
    std::int64_t b2 = (std::int64_t)(b * 100.0);
    std::cout << a * b2 / 100 << std::endl;
}

Pythonによる実装：

a, b = input().split()
a = int(a)
b = int(float(b) * 100)
print(a * b // 100)

解説

残念ながら、このコードも誤答です。

その辺に転がっている浮動小数点数は2進で表されています。10進小数として有限桁で表すことのできる数であっても、2進小数では有限桁で表現できるとは限りません。

例えば、 0.1 は2進浮動小数点数で正確に表現することができません。「0.1 を 10回足してもきっかり 1.0 にはならない」という話は有名かと思います。

ですので、入力の B を2進浮動小数点数として読み取った段階で誤差が発生します。

さらにそれを100倍した際にも誤差が発生するので、 b * 100.0 が本来の値（整数）と一致するかは運次第（入力と、精度に依存する）ということになります。

具体例として、 0.07 を 100 倍すると 7 よりもほんの少し大きな数になりますし、 0.29 を 100 倍すると29 よりもほんの少し小さな数になります。

>>> 0.07 * 100
7.000000000000001
>>> 0.29 * 100
28.999999999999996

実装例のコードでは整数に変換する際に切り捨てが起こるので、大きくなる方は問題ないのですが、本来の値よりも小さくなってしまうと間違った答えが出力されます。（逆にいうと、切り捨て以外の方法で浮動小数点数を整数に変換すれば多少の誤差に影響されずに正しい答えを出すことができます。詳しくは後述します。）

テストケース

入力：

1000000000000000 9.95

正しい出力：

9950000000000000

誤答例2の実行結果：

9940000000000000

倍精度で 9.95 を 100 倍すると 995.0 ではなく 994.999999999999886... （16進表記で 0x1.f17ffffffffffp+9）となります。

誤答例2改：高精度の浮動小数点数型を使う

誤答例2の問題点は、2進小数を使うことに由来するので、高精度の型を使っても解決しません（特定の入力例については正しい答えを返すようになっても、別の反例が出現します）。

（コンテスト本番では高精度の型を使ったコードを落とすテストケースが用意されていなかったようですが、after_contestとして追加されています。正直言って、ちゃんとした浮動小数点数センスの持ち主なら「double じゃなくて long double ならいけるかも」とは考えないので、出題者がこれを落とすためのケースを事前に用意できなかったのは仕方ないかもしれません。）

例えば、80ビット（精度64ビット）の long double では 0.07 の100倍や 0.29 の100倍は正確に計算できるように見えますが、 0.53 の 100 倍がうまくいかなくなります。たとえ四倍精度（精度113ビット）を使ってもこの問題は発生します。

同じ理由で、誤答例1を long double に変えたものもうまくいきません。

実装例

誤答例2のC++による実装を、 long double を使うように変えてみました：

#include <iostream>
#include <cstdint>
#include <cfloat>

static_assert(LDBL_MANT_DIG >= 64, "このコードは long double が80ビット以上の環境を想定しとるのじゃ、すまんな (´・ω・｀)");

int main()
{
    std::int64_t a;
    long double b;
    std::cin >> a >> b;
    std::int64_t b2 = (std::int64_t)(b * 100.0L);
    std::cout << a * b2 / 100 << std::endl;
}

誤答例1の long double 版も用意しておきます：

#include <iostream>
#include <cstdint>
#include <cfloat>
#include <cmath>

static_assert(LDBL_MANT_DIG >= 64, "このコードは long double が80ビット以上の環境を想定しとるのじゃ、すまんな (´・ω・｀)");

int main()
{
    long double a, b;
    std::cin >> a >> b;
    std::cout << (std::int64_t)std::floor(a * b) << std::endl;
}

テストケース

入力：

1000000000000000 8.86

正しい出力：

8860000000000000

誤答例2改の実行結果（long double が80ビットの場合）：

8850000000000000

誤答例1改の実行結果（long double が80ビットあるいは四倍精度の場合）：

8859999999999999

ここから余談：

8.86 を long double で表すと 8.86 よりもほんの少し小さい値になるので、
$$\langle\text{8.86に最も近い long double 値}\rangle \times 10^n$$
を long double で計算した結果は本来の値よりと等しい、もしくは小さい結果になりがちです。実際、上記の実行結果は 8.86 * 100.0 と 8.86 * 10¹⁵ がそれぞれ本来の値よりも小さくなったことによるものです。しかし、掛け算の際に2回目の丸めが起こるので、結果として本来の値よりも大きい値が出てくることもあり得ます。実際、8.86 * 10³⁰ を long double で計算してみると 8860000000000000000079993765888 という、本来の値よりもほんの少し大きい数が得られます（この数は $8.86\times 10^{30}$ に最も近い long double の値です）。

：ここまで余談

誤答例3：1000倍する

誤答例2をちょっと変えて1000倍にしたらACした、みたいな話があります。ですが、これまでの説明でお分かりかと思いますが、1000倍したらACしたというのは偶然にすぎません。

（コンテスト本番では1000倍するコードを落とすテストケースが用意されていなかったようですが、after_contestとして追加されています。正直言って、ちゃんとした浮動小数点数センスの持ち主なら「100倍じゃなくて1000倍したら誤差が減るかも」などとは考えないので以下略）

符号付き64ビット整数では $A\times B \times 100$ 程度なら問題なく表せますが、 $A\times B\times 1000$ となるとオーバーフローしてしまうので注意しましょう。符号なし64ビット整数なら大丈夫です。

実装例

C++による実装：

#include <iostream>
#include <cstdint>

int main()
{
    std::uint64_t a;
    double b;
    std::cin >> a >> b;
    std::uint64_t b2 = (std::uint64_t)(b * 1000.0);
    std::cout << a * b2 / 1000 << std::endl;
}

Pythonによる実装：

a, b = input().split()
a = int(a)
b = int(float(b) * 1000)
print(a * b // 1000)

テストケース

入力：

999999999999999 8.19

正しい出力：

8189999999999991

誤答例3の実行結果（上から4桁目に注目）：

8188999999999991

実際、 8.19 * 1000.0 は（倍精度では） 8190 ではなく 8189.999... となります。

正答例

いくつかの誤答例とそれが誤答である理由を解説しましたが、じゃあどうやったら正答になるのかを見ていきましょう。

有理数の誤差なし計算

正確な有理数演算ができる言語なら、それを使えば誤差のない計算ができます。

一般に、多倍長整数を使った有理数演算は機械組み込みの浮動小数点数演算と比べてコストがかかります。今回の問題のように一発計算するだけなら問題はありませんが、大量の入力を扱う問題ではTLEする可能性があるので注意しましょう。（実際、同じコンテストの B 問題がまさに「何も考えずに多倍長整数で計算するとTLEする」問題でした。）

Pythonによる実装例

Pythonでは fractions モジュールで有理数演算が提供されているようです。

• fractions — Rational numbers

from math import floor
from fractions import Fraction
a, b = input().split()
a = int(a)
b = Fraction(b)
print(floor(a * b))

Haskellによる実装例

Haskell標準の有理数型は Rational ですが、 Rational 型に関する read は小数表記を受け付けません。小数を Rational として読み取るには、 Numeric モジュールの readFloat 関数を使います。

{-# LANGUAGE TypeApplications #-}
import Numeric (readFloat)

main = do
  [s,t] <- words <$> getLine
  let a = read @Integer s
      [(b,"")] = readFloat @Rational t
  print (truncate $ fromInteger a * b :: Integer)

10進小数あるいは固定小数点数を使う

今回は10進小数を正確に扱うことができれば良いので、有理数にこだわらなくても、小数点以下2桁の10進小数を正確に表現できる型を使えば問題ありません。

TODO: COBOLに言及する

Pythonによる実装例

Pythonの場合は decimal モジュールで10進小数を扱えます。精度等の詳しいことはドキュメントを参照してください。

• decimal — Decimal fixed point and floating point arithmetic

from math import floor
from decimal import Decimal
a, b = input().split()
a = int(a)
b = Decimal(b)
print(floor(a * b))

Haskellによる実装例

Haskell (GHC) には標準では10進浮動小数点数はなさそうですが、GHC に付属する Data.Fixed モジュールに固定小数点数型が用意されています。10進で小数点以下2桁の場合は Centi 型を使えます。

• Data.Fixed

{-# LANGUAGE TypeApplications #-}
import Data.Fixed

main = do
  [s,t] <- words <$> getLine
  let a = read @Integer s
      b = read @Centi t
  print (truncate $ fromInteger a * b :: Integer)

C++による実装例

Boost.Multiprecisionに10進浮動小数点数型があります。

• Boost.Multiprecision

#include <iostream>
// #include <cstdint>
#include <boost/multiprecision/cpp_dec_float.hpp>

int main()
{
    boost::multiprecision::cpp_dec_float_50 a, b;
    std::cin >> a >> b;
    std::cout << llround(floor(a * b)) << std::endl;
    // (std::int64_t)floor(a * b) doesn't work :(
}

Boost.Multiprecisionには他にも多倍長整数や有理数、任意精度の2進浮動小数点数型などが用意されているようです。

Cによる実装例

C/C++の人は、 _Decimal128 なり std::decimal::decimal128 なりが将来の標準に入ってその辺の処理系で使えるようになるのを待ちましょう。

次期C標準にはIEEE 754で規定されている10進小数フォーマットに対応する型が規定されるようです。今のGCCも部分的に動くようなので書いてみました。

IEEE 754で規定されているdecimal64は16桁、decimal128は34桁の精度があるようなので、今回の問題についてはdecimal128に対応する型を使えば大丈夫です。

// x86_64 上の Linux 向けの GCC ではコンパイルは通るが、
// scanf 等のライブラリー関数が10進浮動小数点数に対応していないので現状は動かない。
// cf. https://gcc.gnu.org/onlinedocs/gcc/Decimal-Float.html#Decimal-Float

#define __STDC_WANT_IEC_60559_DFP_EXT__
#include <stdio.h>
#include <stdint.h>
#include <inttypes.h>
#include <math.h>

int main(int argc, char *argv[])
{
    int64_t a;
    _Decimal128 b;
#if 0
    // 将来的に使えるようになるはずの書き方
    scanf("%" SCNd64 " %DDf", &a, &b);
#else
    // 現行のGCCは _DecimalNN の入出力に対応していないので手動で読み込む
    {
        int d1, d2;
        scanf("%" SCNd64 " %d.%d", &a, &d1, &d2);
        int d = d1 * 100 + d2;
        b = (_Decimal128)d / 100.0DL;
    }
#endif
#if 0
    // 10進小数として掛け算する
    printf("%" PRIi64 "\n", (int64_t)floord128((_Decimal128)a * b));
#else
    // 100倍の計算に10進小数を使う
    int64_t bb = (int64_t)(b * 100.0DL);
    printf("%" PRIi64 "\n", a * bb / INT64_C(100));
#endif
}

浮動小数点数を正しく丸める

誤答例2の解説で「b * 100.0 が本来の値（整数）と一致するかは運次第」と書きましたが、 b * 100.0 が本来の値に極めて近いことは確実です。そこで、「b * 100.0 に最も近い整数」を計算すれば誤差に影響されずに正しい答えを出せます。

個人的には、誤答例2を「修正」する方向で解法を考えるならこれが一番自然かと思います。

C++による実装例

C/C++では浮動小数点数型を整数型にキャストする際は切り捨てが行われます。浮動小数点数を整数型に変換する際に切り捨てではなく四捨五入するには、 (l)lround を使います。あるいは、 round によって「一番近い整数に対応する浮動小数点数」に変換してから整数型にキャストするのでも良いでしょう。

（四捨五入は、浮動小数点数の計算でおなじみの最近接偶数丸めとは異なります。浮動小数点数の丸めと同じやり方で整数へ変換するには、 nearbyint, rint, lrint, llrint のいずれかを使います。）

math.h

// 四捨五入
double        round(double x);
long int      lround(double x);
long long int llround(double x);

// 丸め
double        nearbyint(double x); // 浮動小数点数例外が出ない
double        rint(double x);      // 浮動小数点数例外が出る
long int      lrint(double x);
long long int llrint(double x);

ヘッダの #include が面倒な人は単に + 0.5 してから整数へキャストするのでも良いかもしれません。（一般論としては、たとえ正の数であっても「+ 0.5 してから切り捨て」した結果は「最も近い整数」となるとは限りません¹。今回はもとの数が整数に近いのでうまくいきます。）

#include <iostream>
#include <cstdint>
#include <cmath>

int main()
{
    std::int64_t a;
    double b;
    std::cin >> a >> b;
#if 1
    // 四捨五入する
    std::int64_t b2 = (std::int64_t)std::llround(b * 100.0);
#else
    // + 0.5 してから切り捨てる（b * 100.0 が整数に近いのでうまくいく）
    std::int64_t b2 = (std::int64_t)(b * 100.0 + 0.5);
#endif
    std::cout << a * b2 / 100 << std::endl;
}

Pythonによる実装例

Pythonの場合は int() は浮動小数点数の入力を（絶対値が小さくなるように）切り捨てますが、 round() を使えば「最も近い整数」に変換することができます。この際、四捨五入ではなく偶数丸めが行われます。

>>> round(6.5) # 四捨五入ではない（四捨五入であれば結果が 7 になるはず）
6

C/C++の場合は「浮動小数点数からの変換結果の整数が組み込みの固定長整数型で表せるとは限らない」ために返り値の型に応じて round 系の関数が複数用意されていましたが、Pythonには多倍長整数があり整数のオーバーフローの心配がないので、 round 関数は単に整数を返すようになっています。

• int() のドキュメント
• round() のドキュメント

a, b = input().split()
a = int(a)
b = round(float(b) * 100)
print(a * b // 100)

Haskellによる実装例

Haskellで浮動小数点数に最も近い整数を得るには、 round 関数を使います。Haskellの round 関数も偶数丸めを行います。Haskellも標準で多倍長整数型を持っているので、 round 関数は（浮動小数点数型ではなく）整数型を返すようになっています。

{-# LANGUAGE TypeApplications #-}

main = do
  [s,t] <- words <$> getLine
  let a = read @Integer s
      b = read @Double t
      bb = round (b * 100.0) :: Integer
  print $ a * bb `quot` 100

小数点を無視して整数として読み取る

浮動小数点数にはうんざりだが言語の標準に有理数や固定小数点数が用意されていない、という場合は、単に読み取る際に小数点をスキップして100倍された整数として扱うのでも良いでしょう。今回のテストケースの入力では末尾の桁が 0 であっても省略せずに所定の桁数が与えられるはずです。

今回は入力の小数点以下の桁数があらかじめわかっているので簡単に実装できますが、一般の小数を読み取る際には別途小数点以下の桁数を数えたりする必要があるので注意してください。また、言語によっては文字列を整数に変換する際に先頭が 0 だと8進数扱いされるので気をつけましょう。

Pythonによる実装例

a, b = input().split()
a = int(a)
b_int, b_frac = b.split(".")
bb = int(b_int) * 100 + int(b_frac)
print(a * bb // 100)

C言語による実装例

scanf で %d.%d という風にフォーマットを指定すると小数点の前後をそれぞれ整数として読み取ることができます。整数を読み取るフォーマット指定子としては %i もありますが、こちらは先頭が 0x の場合16進数、 0 から始まる場合は8進数扱いされるので今回は使えません。

#include <stdio.h>
#include <stdint.h>
#include <inttypes.h>

int main(int argc, char *argv[])
{
    int64_t a;
    int64_t bb;
    {
        int d1, d2;
        scanf("%" SCNd64 " %d.%d", &a, &d1, &d2);
        bb = d1 * 100 + d2;
    }
    printf("%" PRIi64 "\n", a * bb / INT64_C(100));
}

参考：ABC 169 C - Multiplication 3 にみる浮動小数点の取り扱い方 - 私のひらめき日記

テストケースまとめ

これまで登場した誤答例を落とすためのテストケースをまとめておきます。

これらのテストケースを生成するに使ったコードは https://gist.github.com/minoki/0e4ebcee49d540ede29f26a0025903ca に置いておきます。地味に _Float128 を使っているので、C言語で四倍精度を使ったコードに興味がある方は読んでみると良いかもしれません。

---

入力例X-1：

999999999999900 9.25

出力例X-1：

9249999999999075

---

入力例X-2：

1000000000000000 9.95

出力例X-2：

9950000000000000

---

入力例X-3：

1000000000000000 8.86

出力例X-3：

8860000000000000

---

入力例X-4：

999999999999999 8.19

出力例X-4：

8189999999999991

---

この記事で登場した誤答例と、それを落とすためのテストケースの対応表を用意しておきます。一つの反例が複数の誤答を落とすこともあります。

	X-1	X-2	X-3	X-4
誤答例1（倍精度）	💣		💣
誤答例1改（80ビット）			💣
誤答例1改（四倍精度）			💣
誤答例2（倍精度）		💣		💣
誤答例2改（80ビット）			💣	💣
誤答例2改（四倍精度）		💣
誤答例3（倍精度）				💣
誤答例3（80ビット）				💣
誤答例3（四倍精度）				💣

浮動小数点数の闇をもっと知りたい方へ（宣伝）

浮動小数点数に関して、最近こんな記事を書きました：

• 浮動小数点数の min / max

筆者のブログでもちょいちょい浮動小数点数ネタを扱っています：

• 「浮動小数点数」タグのついた記事

---

浮動小数点数については「誤差やその他罠があってよくわからん」と思っている方も多いかと思います。筆者としては、一人でも多くの人が浮動小数点数とまともに向き合って、うまく付き合っていけるようになることを願っています。筆者の記事が少しでもその助けになれば幸いです。

おまけ：四倍精度を使った嘘解法

C/C++の long double は環境によって精度がまちまちです。x86_64ターゲットのGCCでは80ビットの拡張倍精度ですが、環境によっては double と同じく64ビットだったり、あるいは四倍精度だったりします。

一方、最近のGCCでは __float128 あるいは _Float128 という型名で四倍精度浮動小数点数（指数部15ビット、仮数部113ビット）を使うことができます。x86_64ではまだ四倍精度がハードウェア実装されていないので、ソフトウェア的に計算することになりますが、お試しなら問題ないでしょう。

• 6.12 Additional Floating Types

ということで、 long double が80ビットな環境で四倍精度を使った嘘解法を試してみたいと思います。

浮動小数点数の数学関数や入出力に関しては別途 libquadmath が必要になりますが、AtCoderのGCCでは libquadmath は使えません。そこで、今回は入力の B を整数で読み取ってから自前で _Float128 に変換してみます。（もちろん、真面目に問題を解くのであれば B を整数として読み取ってからわざわざ浮動小数点数に変換するのは本末転倒です。なのでこれはあくまでお遊びです。）

#include <stdio.h>
#include <stdint.h>
#include <inttypes.h>
#include <math.h>

int main(int argc, char *argv[])
{
    int64_t a;
    _Float128 b;
    {
        // 手動で読み込む
        int d1, d2;
        scanf("%" SCNd64 " %d.%d", &a, &d1, &d2);
        int d = d1 * 100 + d2;
        b = (_Float128)d / 100.0F128;
    }
#if 1
    // 誤答例1：浮動小数点数として掛け算する
    // 精度の問題はないが、2進なので結局ダメ
    printf("%" PRIi64 "\n", (int64_t)((_Float128)a * b));
#elif 1
    // 誤答例2：浮動小数点数として100倍する
    int64_t bb = (int64_t)(b * 100.0F128);
    printf("%" PRIi64 "\n", a * bb / INT64_C(100));
#else
    // 誤答例3：1000倍する
    uint64_t bb = (uint64_t)(b * 1000.0F128);
    printf("%" PRIu64 "\n", a * bb / UINT64_C(1000));
#endif
}

拡張倍精度や四倍精度についてはいずれ改めて記事を書きたいと思っています。

1. コメントで紹介された記事 PHPのround関数とは一体なんだったのか - hnwの日記 を参照してください。 ↩