はじめに
今回は
の続き。満を持してk-means法を使って減色をする。
画像は引き続きレナ嬢とする。
| lenna.png |
|---|
 |
減色する
クラスタリング
まずは途中までのコードを示す。「コード1」~「コード4」は順々に追記していってほしい。
コード1は教科書的なクラスタリングだ。
import numpy as np
import cv2
import matplotlib.pyplot as plt
filename = "lenna.png"
image = cv2.imread(filename)
Z = image.reshape((-1, 3)) # (h, w, 3) -> (h*w, 3) にする
Z = Z.astype(np.float32) # uint8 -> float32にする
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 10, 1) # 計算終了条件
K = 4 # クラスター数
# クラスタリング
compactness, labels, centers = cv2.kmeans(Z, K, None, criteria, 10, cv2.KMEANS_RANDOM_CENTERS)
現段階では何かを出力するようなコードではないが、VS Codeで最後で停止するなどしてさまざまな値を確認してみよう。
image.shape
(512, 512, 3)
Z.shape
(262144, 3)
labels.shape
(262144, 1)
labels
[[2]
[2]
[2]
...
[3]
[3]
[3]]
centers
[[162.94193 184.51288 228.4131 ]
[ 68.62079 28.145124 100.21161 ]
[113.52266 120.815994 211.41876 ]
[ 88.29044 72.26667 169.50961 ]]
labelsはZの各要素に付与されたラベル。各ラベルの具体的な値がcentersにあるK個の要素。
だからラベルの配列をBGR値の配列に戻して、あらためて(h, w, 3)にリシェイプしてやれば減色された画像を得ることができるはずだ。
ファンシーインデックス
ところでラベルの配列をBGR値の配列にするのはどうしたらよいのだろう。
もちろんforループを回してもよいが、numpyにはリストで要素を指定するという方法がある。
多くの解説サイトではここはあっさりと記述しているが、私にはこの挙動は何がなんだかさっぱりわからなかった。
どうやらこれはファンシーインデックスという、らしい。
用語がわかれば検索してより詳しい説明を得ることもできる。
たとえばこんなnumpy配列があるとしよう。
letters = np.array(["A", "B", "C", "D", "E", "F", "G", "H", "I",
"J", "K", "L", "M", "N", "O", "P", "Q", "R",
"S", "T", "U", "V", "W", "X", "Y", "Z"])
これから次のようにスライスで元配列の要素の一部を取り出すことができる、ということはよく知られている。
スライスはnumpyに限らず普通のリストでもできる。
letters[3:6]
array(['D', 'E', 'F'], dtype='<U1')
それとは別に、インデックスにリストを指定することでそれに応じた要素を持つ新しい配列を返す。これがファンシーインデックスだ。
ファンシーインデックスはリストではできない。numpy独自の機能だ。
letters[[7, 4, 11, 11, 14]]
array(['H', 'E', 'L', 'L', 'O'], dtype='<U1')
クラスタリング結果から画像を作る
ということで、ファンシーインデックスを利用してラベルの配列からBGR値の配列を作り出そう。
事前にファンシーインデックスについて調べたので、ここでは特筆すべきことはない。
labels = labels.flatten() # 一次元にする
centers = centers.astype(np.uint8) # float32 -> uint8にする
result = centers[labels] # ラベルに則った色の配列 ここがファンシーインデックス
result = result.reshape(image.shape) # 元画像と同じシェイプにする
cv2.imshow("result", result)
cv2.waitKey(0)
cv2.destroyAllWindows()
| 元画像 | 減色後 |
|---|---|
 |
 |
もちろんグレースケール画像を減色したり、RGBそれぞれをK段階に減色した全K^3色の減色画像を作ることも可能だ。
代表色を確認する
ヒストグラムと減色結果をあわせて可視化しよう。
前回はRGBを一つのグラフとしたが、今回はそれではわかりづらいので個別のグラフとする。
COLORS = ["blue", "green", "red"]
for i, c in enumerate(COLORS):
hist = cv2.calcHist([image], [i], None, [256], [0, 256])
plt.plot(hist, color=c)
center_colors = [x[i] for x in centers] # K個の色のBGR要素
for j, color in enumerate(center_colors):
plt.axvline(color, color=c)
plt.text(color, 0, f"{j}:{color}")
plt.show()
| BGR | ヒストグラム |
|---|---|
| B要素 | 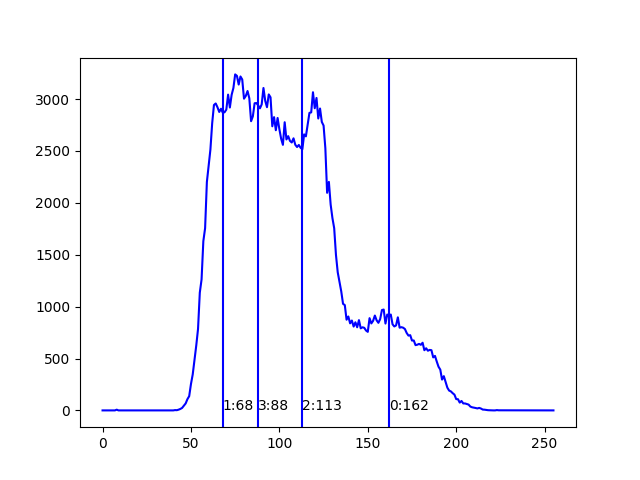 |
| G要素 | 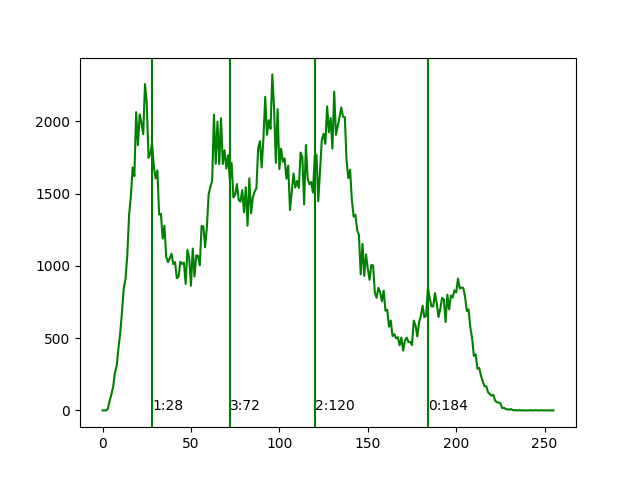 |
| R要素 | 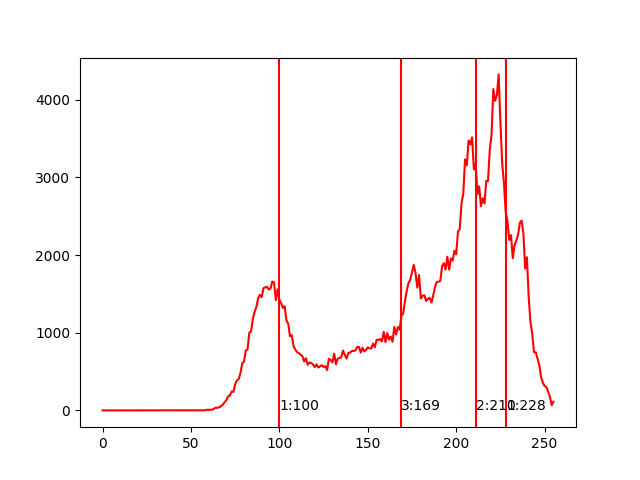 |
この画像には
len(np.unique(Z, axis=0))
148279
から148279色が使われているわけだが、それがrgb(228,184,162)・rgb(100,28,68)・rgb(211,120,113)・rgb(169,72,88)の四つの代表色に減色されたことがわかる。
代表色が変わる境界線を調べる
ここまで来たら、代表色の範囲および境界線を可視化したくなった。
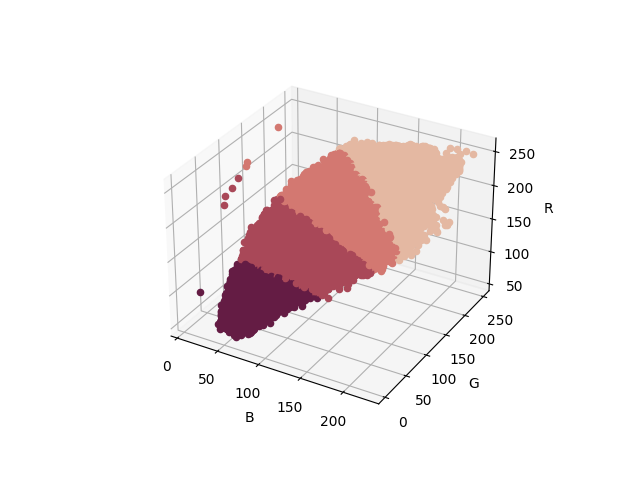
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.set_xlabel("B")
ax.set_ylabel("G")
ax.set_zlabel("R")
for (b, g, r), label in zip(Z, labels):
ax.scatter(b, g, r, color=centers[label][::-1]/255) # 色は0~255でなく0.0~1.0で指示する
plt.show()
結果はこうだ。512×512=262144個のBGR値をプロットするのにものすごく時間がかかった。
OpenCVのBGRをRGBに直すのを忘れてやり直すことになって泣きたくなった。
境界線はまっすぐになっているわけではない。k-means法は計算を繰り返して条件を満たしたら終了するという処理をしているからだろう。
終わりに
cv2.kmeans()を使って減色させました、だけでなく、さまざまな知見を得ることができた。
「numpy インデックス リスト」などと検索してファンシーインデックスなる言葉を知っとき、新たな世界の扉が開いたものだ。