はじめに
この記事は、Unityを通して3Dモデルのスキニングを理解するためのものです。(若干エンジニア向けな内容です。)
まず、3DCGでは3Dモデルを動かす際にボーンを使ってメッシュを変形させるスキニングという手法が一般に用いられます。この記事ではUnityでのスキニングを行っているSkinnedMeshRendererを例に、どのようにスキニングが行われているかを説明します。
実行環境は以下の通りです。
| 項目 | バージョン |
|---|---|
| OS | Windows 11 |
| Unity | Unity 2022.3.1f1 |
| Unity Rendering Pipeline | Built-in |
| Blender | Blender 3.4 |
スキニングのアルゴリズムの種類
一口にスキニングと言っても、様々な種類があります。
まず、LBS(Linear Blend Skinning) は非常に簡単で計算コストも少ないアルゴリズムで、Unityや多くの3DCGソフトではLBSに基づいてスキニングが行われています。他にも、LBSで腕を大きく曲げた際に肘の体積が減ってしまう問題を解決するために発案されたDQS(Dual Quaternion Skinning)1やSBS(Spherical Blend Skinning)2等もありますが、Unity標準で用意されていないため今回は扱いません。
LBS(Linear Blend Skinning)
LBSを説明するには、ボーン・スケルトン・ウェイト・バインドポーズを理解している必要があります。まず、それぞれの用語について簡単に説明します。
ボーン・スケルトン
ボーンとは、人体の骨のようなもので、ボーンを動かすとそれに応じてメッシュの頂点が変形します。
また、複数のボーンが集まった骨格のようなものをスケルトンと呼びます。

ウェイト
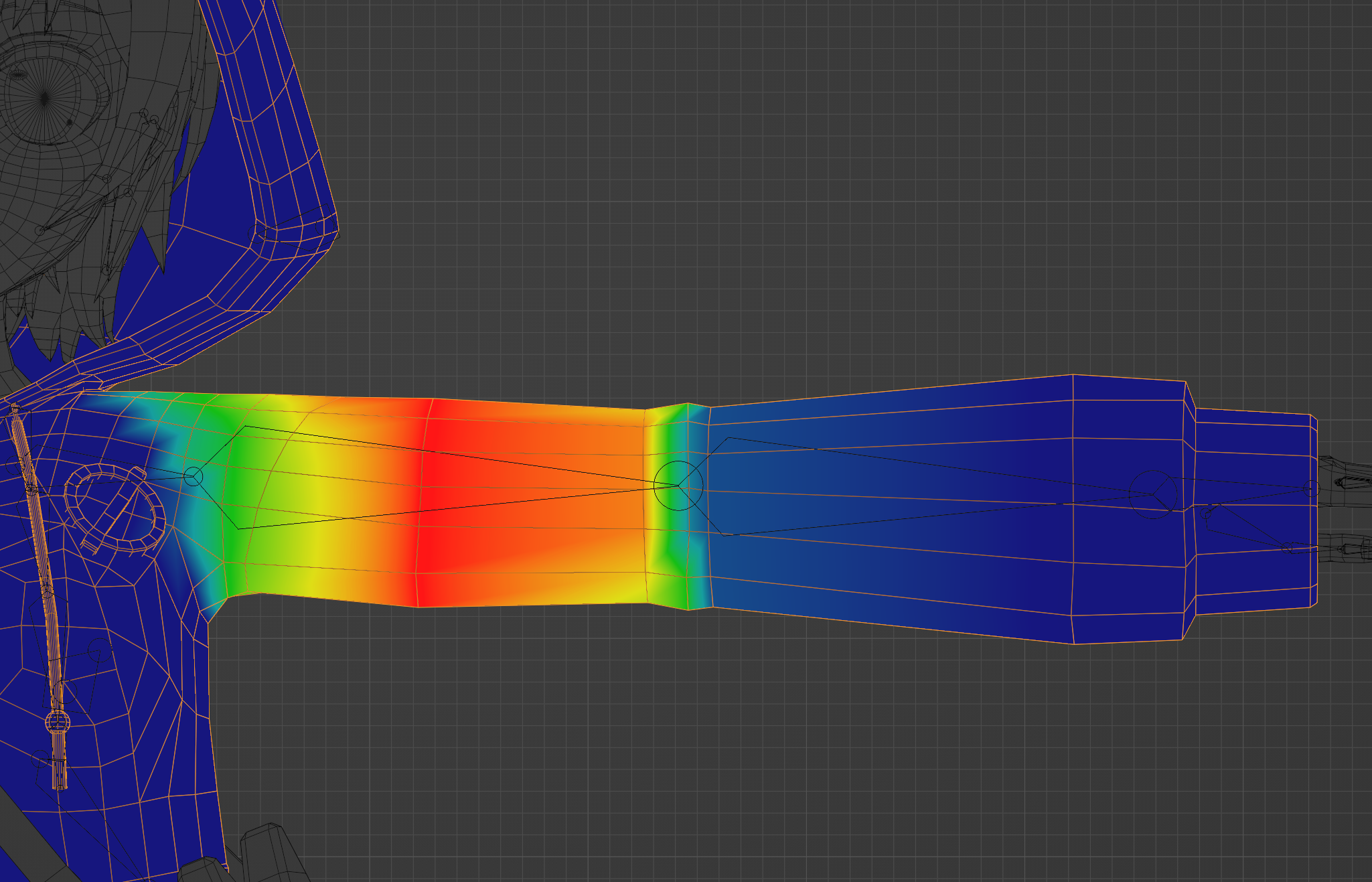
ウェイトとは、各頂点がボーンの移動・回転(・拡大縮小)の影響をどの程度受けるかを表すものです。Blenderでは赤が最も影響を受けていて(ウェイトが1)、青が最も影響を受けていない(ウェイトが0)というように表示されます。
各頂点でのウェイトは、影響を受けている全てのボーンのウェイトを足すと必ず1になるように正規化されます。
バインドポーズ
バインドポーズとは、モデルのメッシュにスケルトン(ボーン)を紐づける(バインドする)ときのポーズです。人体の場合、バインドポーズには主に腕の角度の違いによってTスタンスとAスタンスに分けられます。(画像はスケルトンがTの字をしているためTスタンスです。)

アルゴリズム
各頂点の座標の計算方法
LBSでのメッシュの各頂点の座標は次のように求めることができます。
\begin{equation}
\begin{aligned}
v' &= \sum_{i=0}^{n-1} w_i B'_i B_i^{-1} v
\qquad
\textrm{where} \quad \sum_{i=0}^{n-1} w_i = 1, w_i>0
\end{aligned}
\end{equation}
| 記号 | 意味 |
|---|---|
| $v'$ | LBS後の頂点の座標 |
| $n$ | 頂点に対して影響を与えるボーンの数 |
| $w_i$ | 頂点vに対するi番目のボーンの影響度 |
| $B'_i$ | 現在のi番目のボーンの変換行列 |
| $B_i^{-1}$ | バインドポーズ時のi番目のボーンの逆変換行列 |
| $v$ | バインドポーズ時の頂点の座標 |
各頂点の座標の計算方法(具体例)
数式だけを見ても分かりづらいと思うので具体例を交えて説明します。
この説明では簡単のためx-y平面での座標と回転のみを考えていますが、実際は変換行列を用いるため拡大縮小も考慮されます。
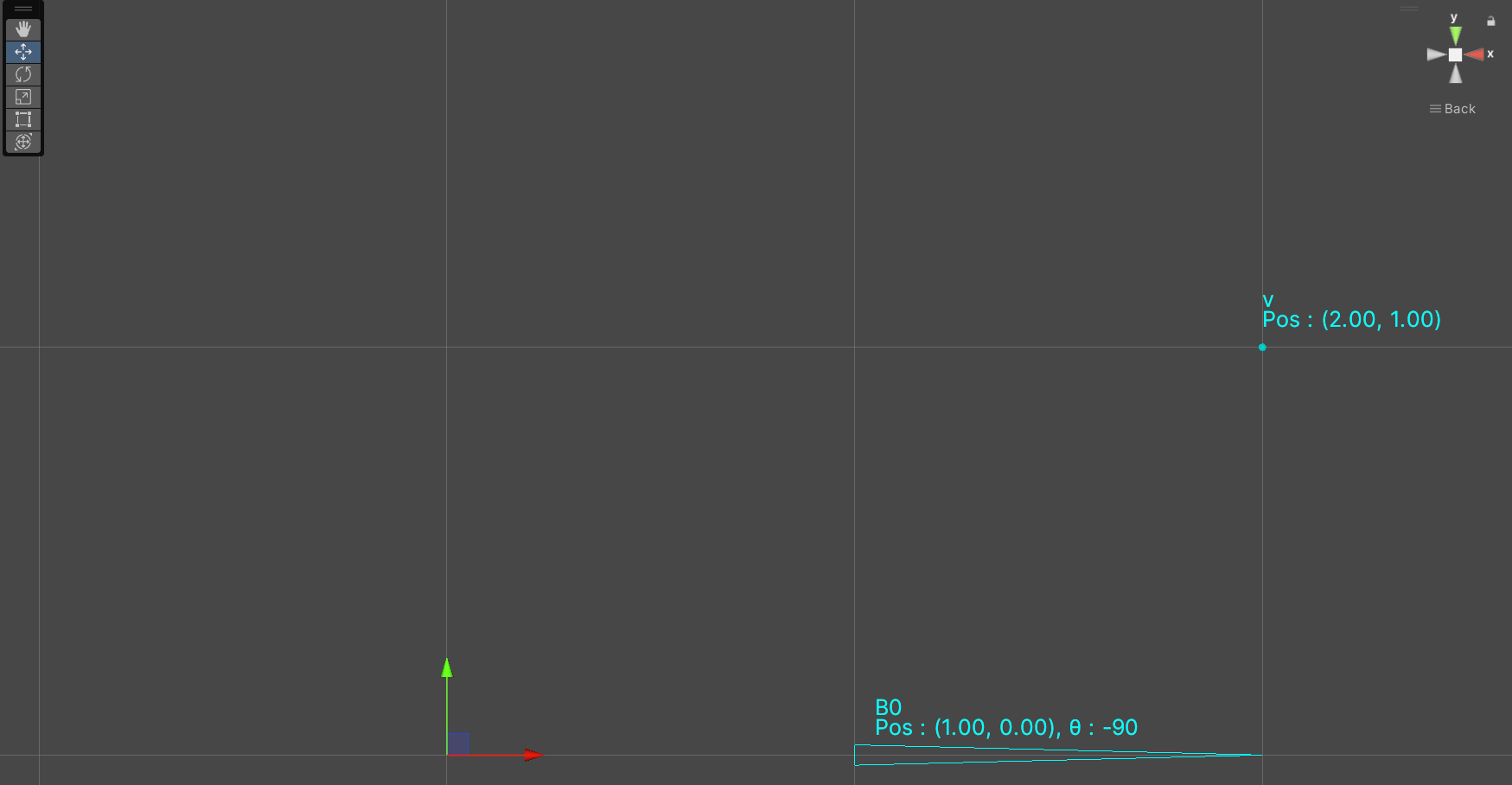
0. バインドポーズ時状態
バインドポーズ時の頂点の座標 : $ v = (2, 1)^\top $
頂点に対して影響を与えるボーンの数 : $ n = 1 $($b_0$のみ)
頂点vに対する0番目のボーンの影響度 : $ w_0 = 1 $
バインドポーズ時のボーンの座標 : $ b_0 = (1, 0)^\top $
バインドポーズ時のボーンの回転(z軸周り) : $ \theta = -90 $
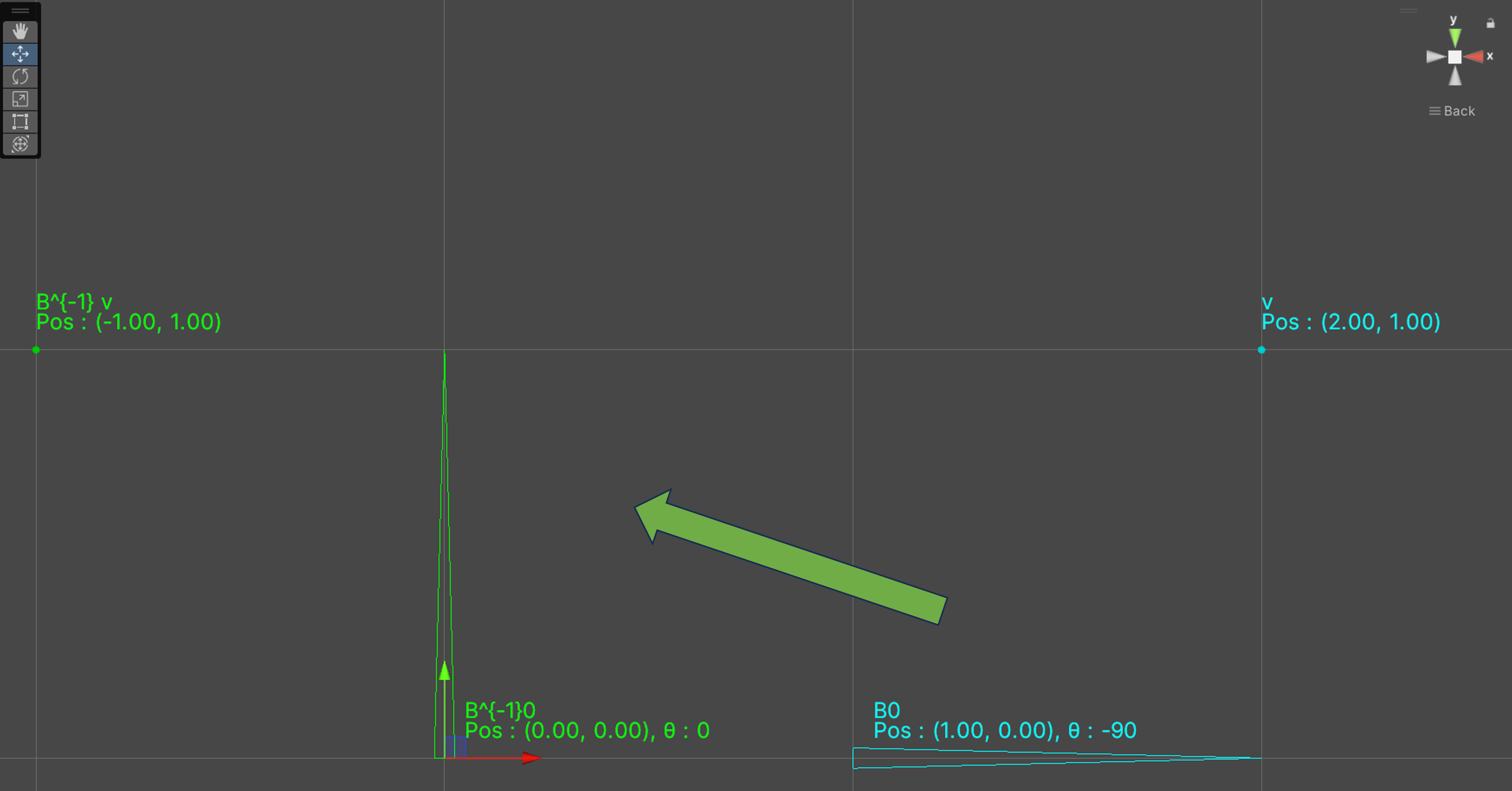
1. バインドポーズ時のボーンを原点で回転が0になるようにする
$ B_i^{-1} v $ : バインドポーズ時のボーンを原点で回転が0の状態にしたときの頂点の座標
つまり、$v$に対して以下の操作を行う
$-b_0 = -(1, 0)^\top$移動する
$$v-b_0 = (2, 1)^\top - (1, 0)^\top = (1, 0)^\top$$
z軸周りで$-\theta=90$回転させる
R(-\theta)(v-b_0) = R(90)(1, 0)^\top =
\begin{pmatrix}
\cos{90} & -\sin{90} \\
\sin{90} & \cos{90}
\end{pmatrix}
(1, 0)^\top
=
(-1, 1)^\top
よって、
$$B_0^{-1} v = R(-\theta)(v-b_0) = (-1, 1)^\top $$となる。
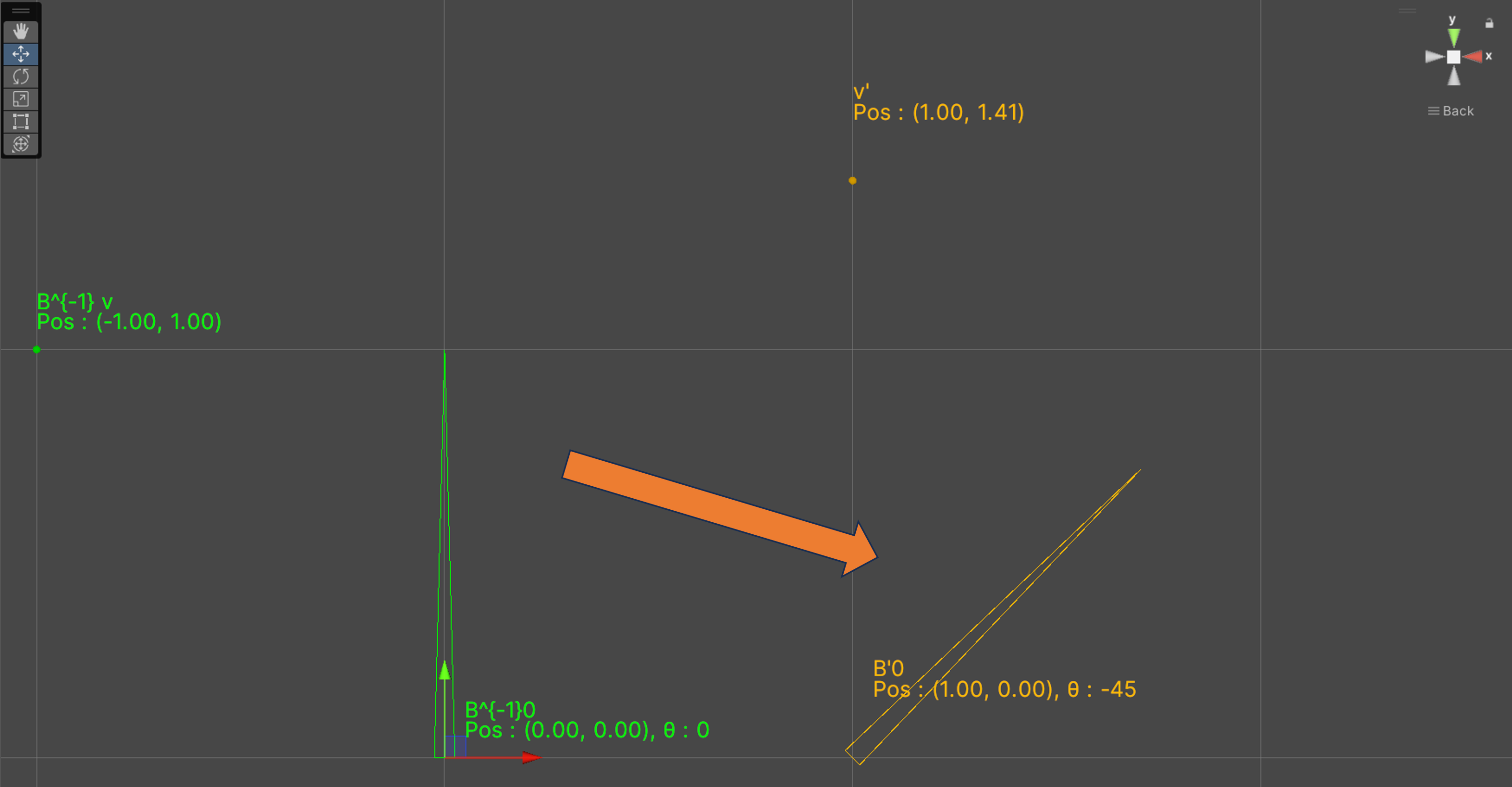
2. 1.で原点に移動させたものを現在のボーンの座標に移動する
$ B'_i B_i^{-1} v $ : 1.で原点に移動させたものを現在のボーンの座標に移動した座標
つまり、$B_0^{-1} v$に対して以下の操作を行う
z軸周りで$\theta'=-45$回転させる
R(\theta')R(-\theta)(v-b_0) v = R(-45)(-1, 1)^\top =
\begin{pmatrix}
\cos{-45} & -\sin{-45} \\
\sin{-45} & \cos{-45}
\end{pmatrix}
(-1, 1)^\top
=
\left(0, \sqrt{2}\right)^\top
$b'_0 = (1, 0)$移動する
R(\theta')R(-\theta)(v-b_0) v + b'_0
=\left(0, \sqrt{2}\right)^\top + (1, 0)^\top
=\left(1, \sqrt{2}\right)^\top
よって、$$v'=B'_i B_i^{-1} v = R(\theta')R(-\theta)(v-b_0) v + b'_0 = \left(1, \sqrt{2}\right)^\top\approx(1,1.41)^\top
$$となる。
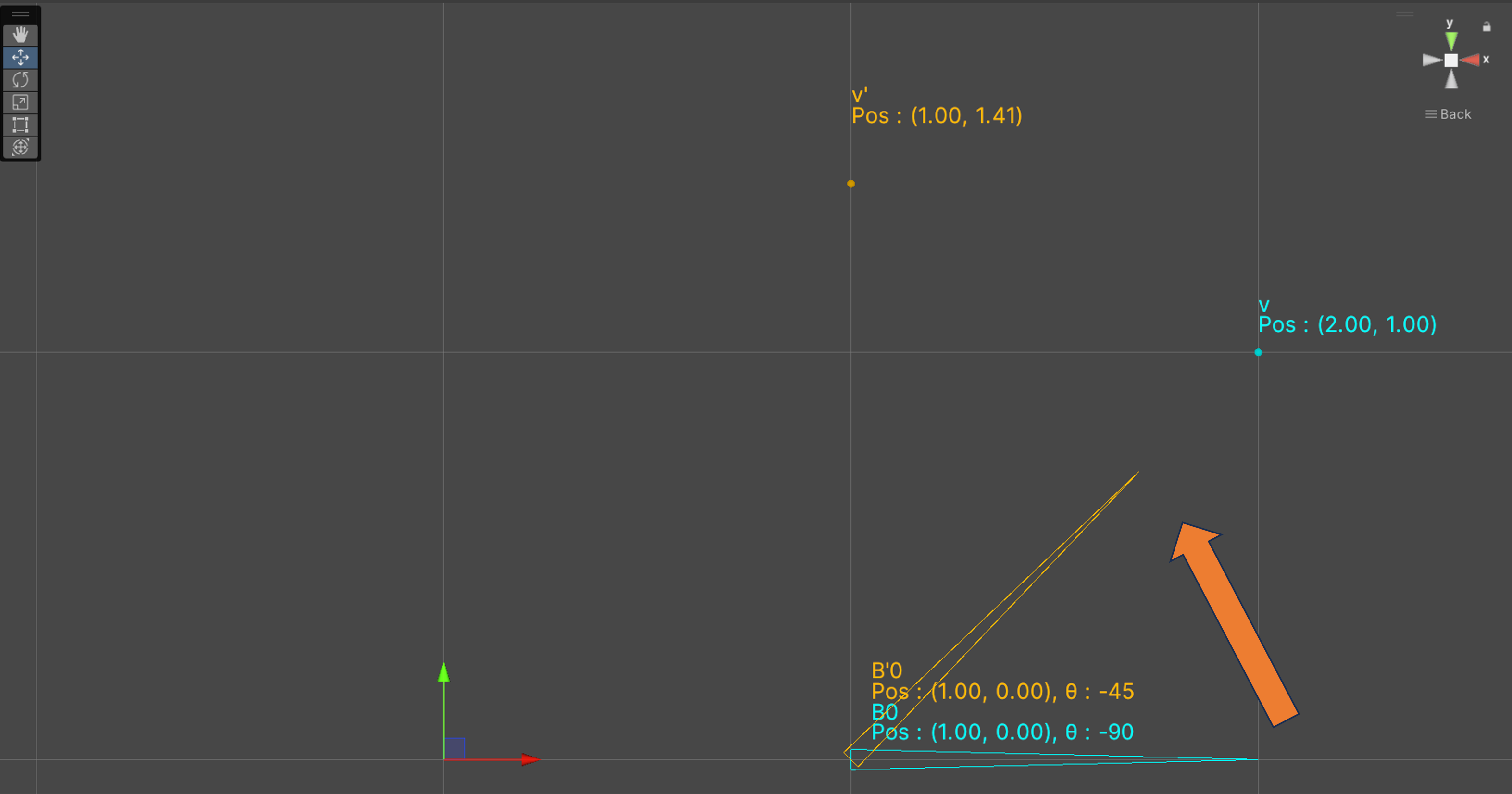
3. 1~2.をボーンの数だけ足し合わせる
$ v' = \sum_{i=0}^{n-1} w_i B'_i B_i^{-1} v $ : 1~2.をウェイトで重み付けした重み付け和
今回は$v$に影響するボーンは$B_0$のみで$w_0=1$なので、$v'\approx(1,1.41)^\top$となる。
以上で、バインドポーズ時の頂点$v'=(2,1)^\top$から現在のボーンの状態の頂点$v'\approx(1,1.41)^\top$を計算することができる。
Unityでの実装
LBSでのスキニングをUnity C#で実装してみました。
コードの全体は以下のGistを参照してください。
SkinnedMeshRendererと同じGameObjectにアタッチすると動作します。
https://gist.github.com/mkc1370/665c29e0b76d3d81bf45f4c6ff303641
コードの説明
先程の式をUnityっぽく(?)書くと次のようになります。
$$ \textrm{vertex} = \sum_{i=0}^{n-1} \textrm{weight[i]} * \textrm{bones[i].localToWorldMatrix}(\textrm{bindposes[i]}(\textrm{bindPoseVertex})) $$
| 記号 | 意味 |
|---|---|
| vertex | LBS後の頂点の座標 |
| n | 頂点に対して影響を与えるボーンの数(今回は4) |
| weight[i] | 頂点vに対するi番目のボーンの影響度 |
| bones[i].localToWorldMatrix | 現在のi番目のボーンの変換行列 |
| bindposes[i] | バインドポーズ時のi番目のボーンの逆変換行列3 |
| bindPoseVertex | バインドポーズ時の頂点の座標 |
Gistの内容と若干異なりますが、メインのLBSの処理内容は以下のコードのようになっています。また、ここでは頂点の座標のみに対してLBSを行っていますが、Gistでは法線に対してもLBSを行っています。
// LBS(Linear Blend Skinning)でのスキニング
for (var vertexIndex = 0; vertexIndex < _currentVertices.Length; vertexIndex++)
{
// 初期化
_currentVertices[vertexIndex] = Vector3.zero;
// 1頂点あたりのボーンのインフルエンス数を5個以上にするとAPI的に処理が面倒なので、簡単のために4個までに制限
var maxBoneWeightCount = 4;
for (var i = 0; i < maxBoneWeightCount; i++)
{
// 頂点に影響するボーンの情報を取得(forで回すためにGetBoneWeightでラップしている)
var (boneIndex, weight) = GetBoneWeight(vertexIndex, i);
// 頂点の座標のブレンド
_currentVertices[vertexIndex] +=
weight * _bones[i].localToWorldMatrix.MultiplyPoint(mesh.bindposes[boneIndex].MultiplyPoint3x4(_bindPoseVertices[vertexIndex]));
}
}
単純なモデルでの動作例
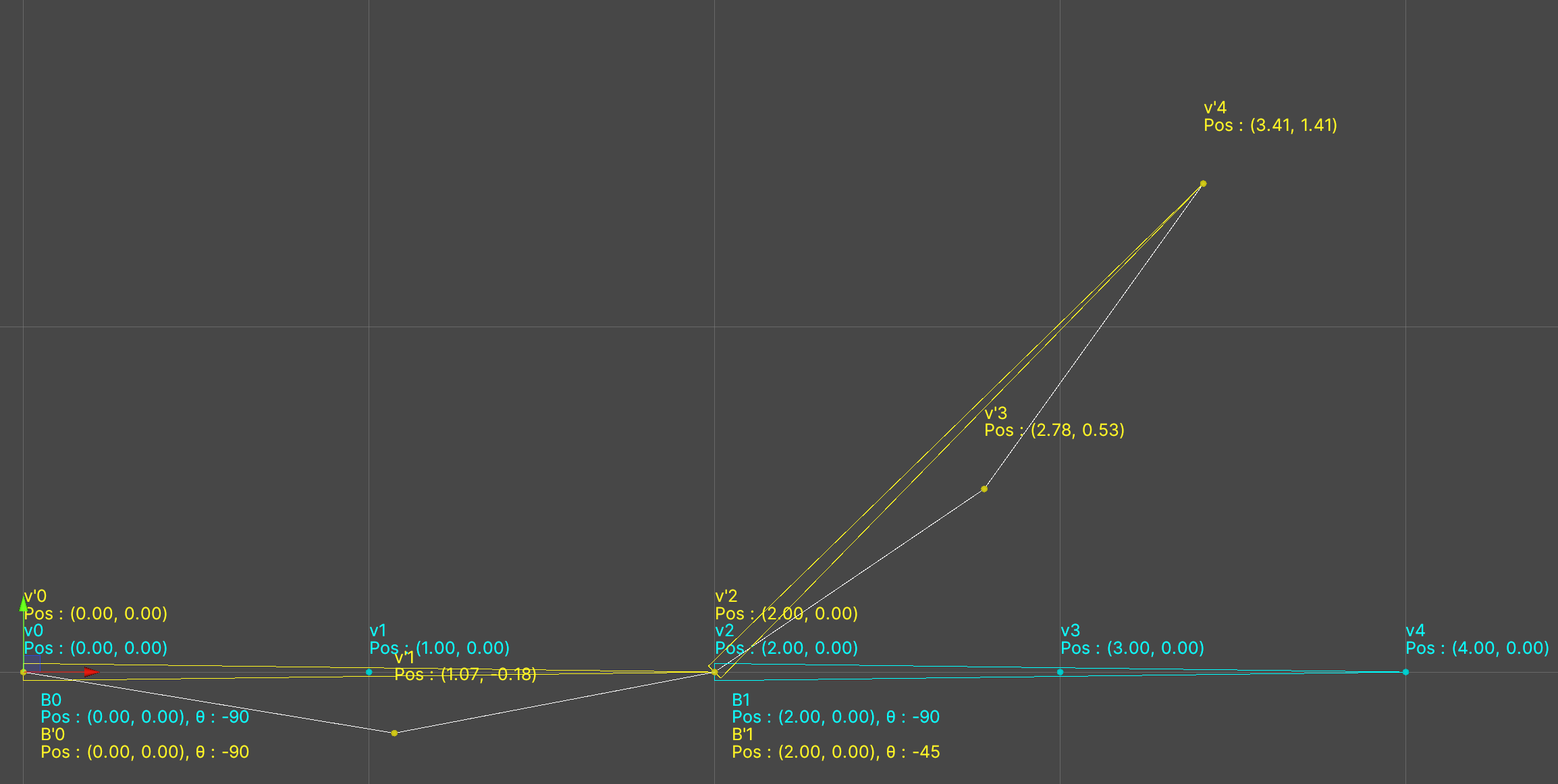
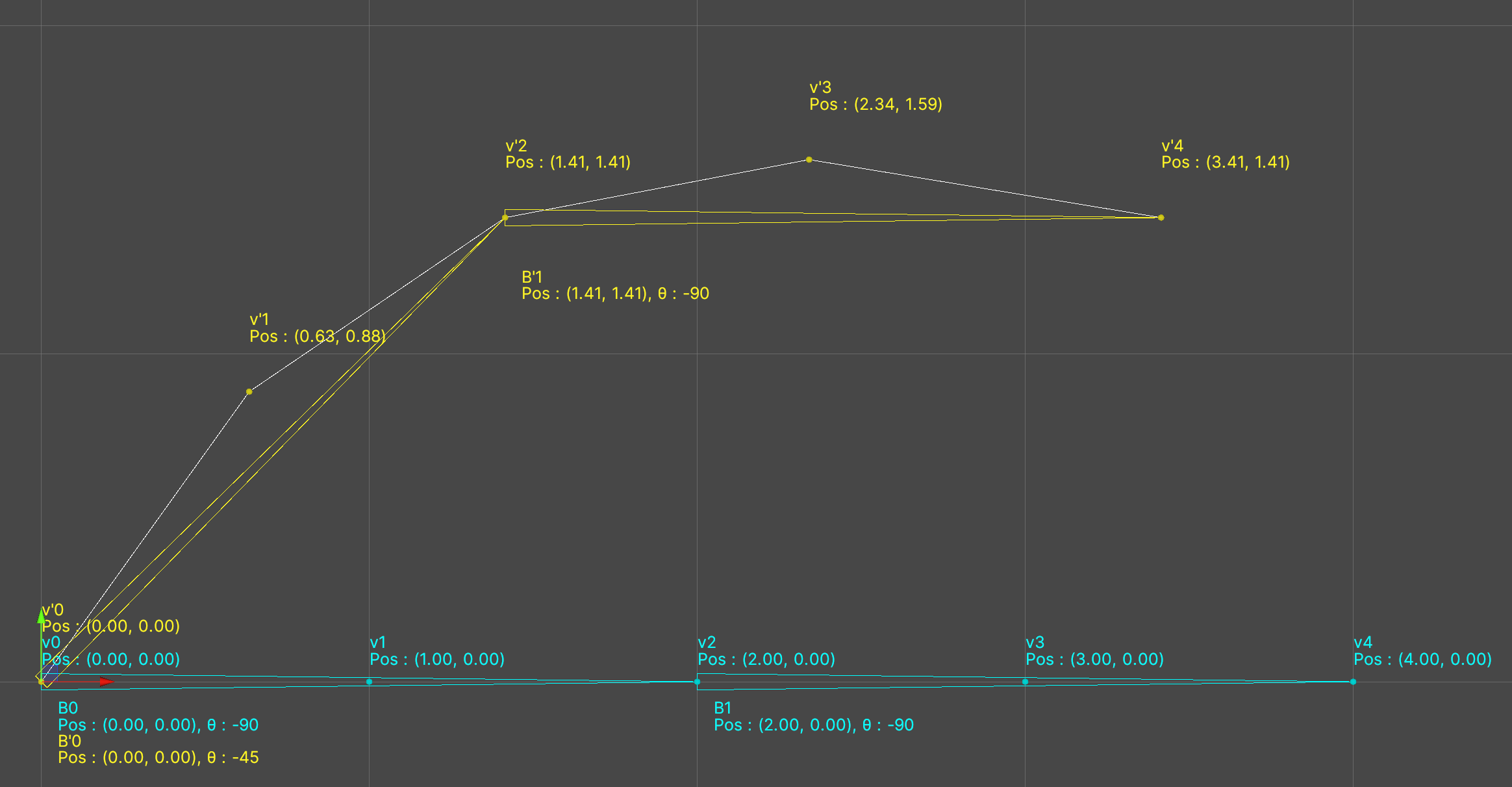
簡単のため、頂点が4個だけのメッシュ(トポロジはLines4)を用意しました。

ボーンの座標・回転は画像のとおりです。ただし、それぞれの頂点のウェイトは表のようにボーンから離れるにつれて小さくなるように設定しました。
| ボーン | v0 | v1 | v2 | v3 | v4 |
|---|---|---|---|---|---|
| B0 | 1 | 0.75 | 0.5 | 0.25 | 0 |
| B1 | 0 | 0.25 | 0.5 | 0.75 | 1 |
3Dモデルでの動作例
ユニティちゃんのunitychan_SLIDE00のモーション5 © UTJ/UCL でスライディングしている様子です。ぱっと見た限りでは同じスキニングを再現できていることが分かります。実際に各頂点の座標の二乗平均平方根誤差を求めたところ、2.64452571331574E-08であったため計算の誤差の範囲内だと思います。
左がUnityのSkinnedMeshRenderer、右が自作のMySkinnedMeshRenderer。

まとめ
今まで何となく理解した気になっていたスキニングでしたが、実際に処理内容を見てみると思ったよりシンプルなものでした。この記事がスキニングへの理解の手助けになれたなら幸いです。
余談 : UnityでのスキニングはGPU?CPU?
ときどき話題に上がる内容ですが、少なくともUnity 2022.3.1f1ではデフォルトでGPUでスキニングが行われます。設定やグラフィックAPIによってはCPUでスキニングが行われることがあります。6(結構昔からUnityのGPUでのスキニングは何かとバグを抱えていたことが多かった印象ですが、最近は安定している気がします。)
[Project Settings]->[Player]->[GPU Compute Skinning]
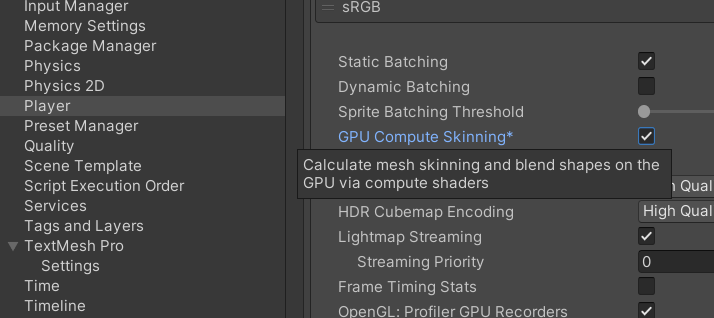
画像から分かるように、GPUでスキニングをする場合はスキニング(とブレンドシェイプ)の計算はコンピュートシェーダーで行われます。
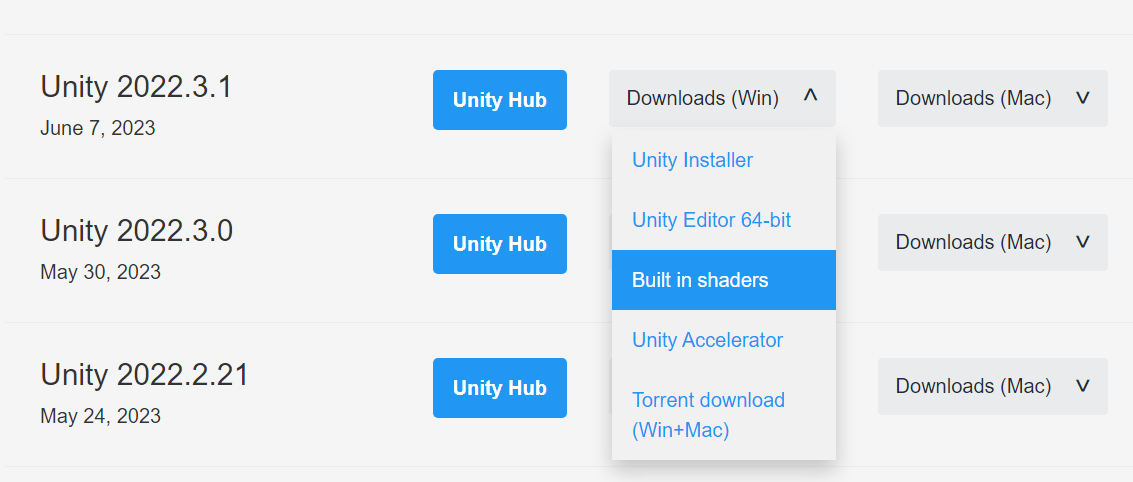
実際のコンピュートシェーダーはUnity download archiveからダウンロードすることができますので、興味のある方は見てみると面白いです。
スキニング : DefaultResources/Internal-Skinning.compute
ブレンドシェイプ : DefaultResources/Internal-BlendShape.compute