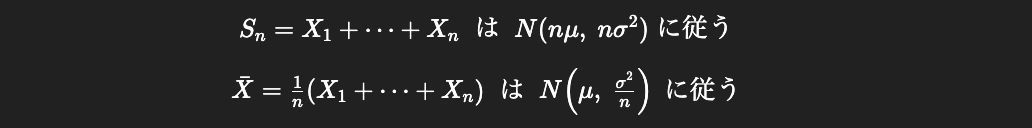自己紹介
- 業務経験10年超えのサーバーサイドWebエンジニア。業務で統計やデータサイエンスを扱ったことはない。
- 大学は経営学部卒。センター試験のための数学1Aと2Bだけ勉強していて、3Cはやっていない。センター試験の結果は1Aと2Bいずれも平均点+15点ぐらいの点数だった。
- 大学でも数学に触れることは無かった。
- 2022年1月から統計検定の勉強を始めた。1カ月で2級(CBT)に77点で合格。
統計検定準1級の受験履歴
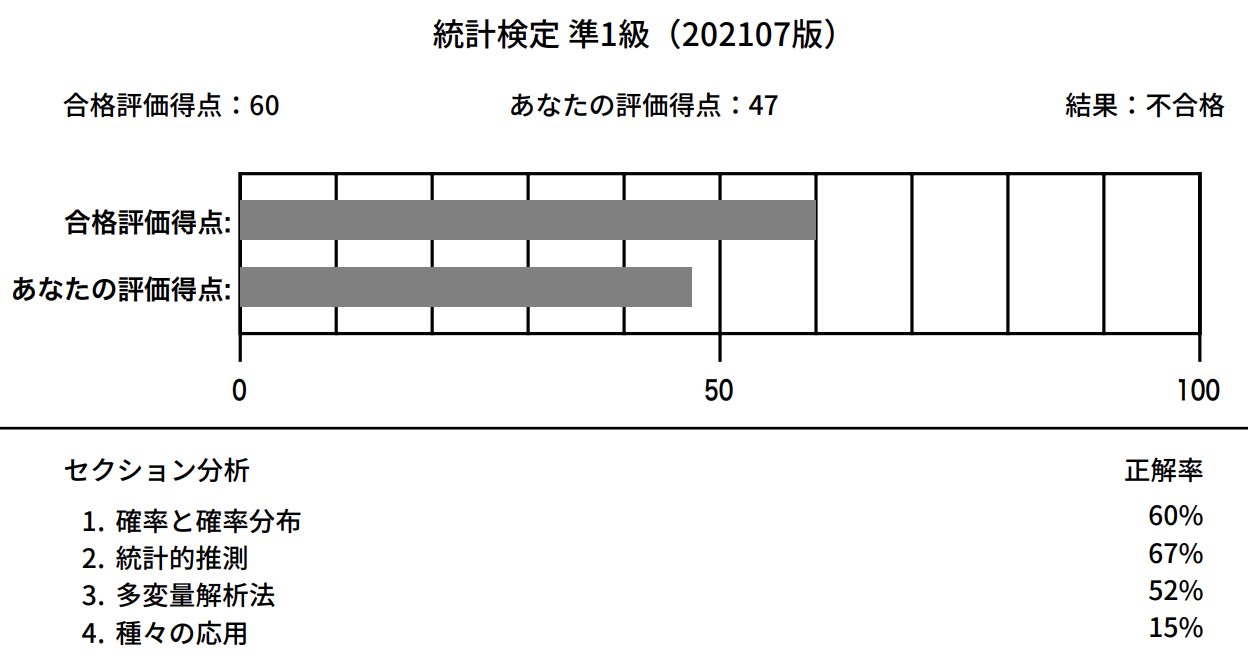
- 2023年5月: 47点で不合格
- 2025年3月: 55点で不合格
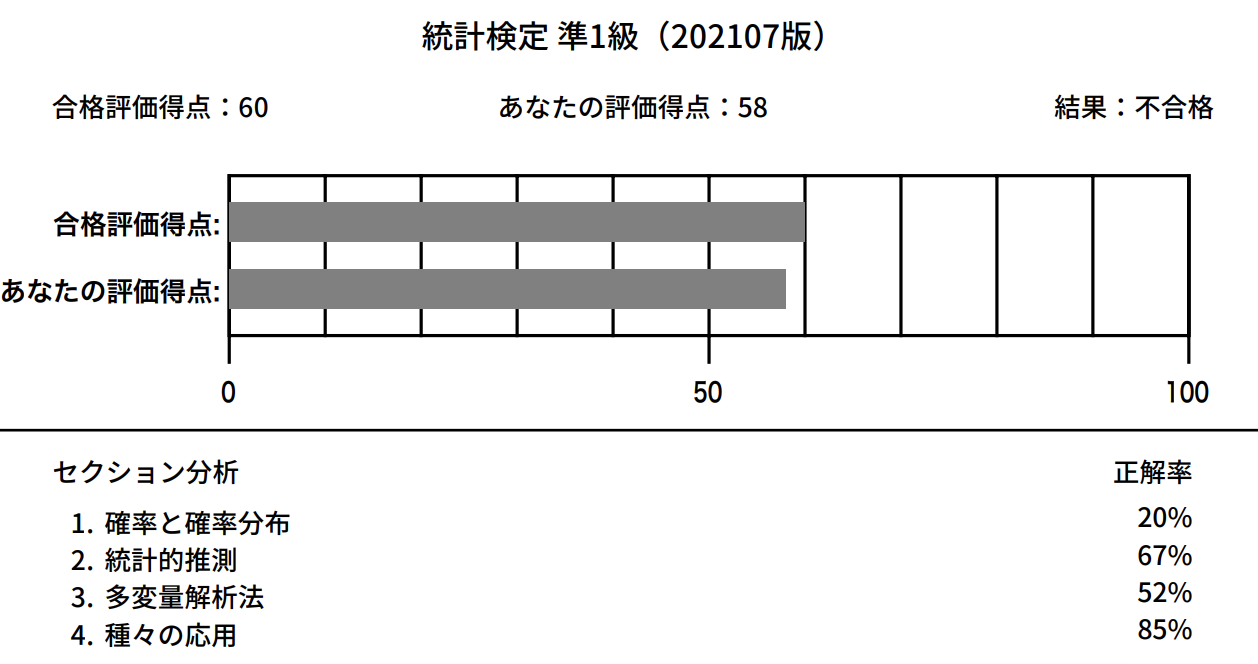
- 2025年7月: 58点で不合格
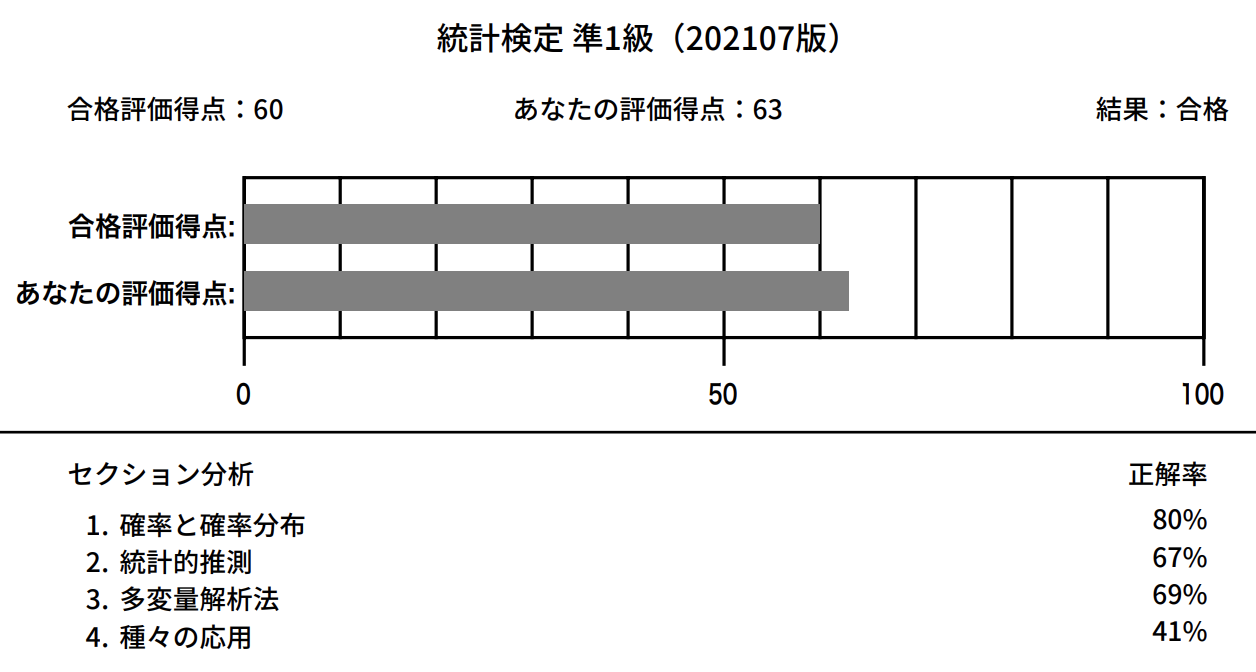
- 2025年8月: 63点で合格
勉強内容
| 時期 | 内容 | 勉強時間概算 |
|---|---|---|
| 2022年2月〜6月 | 初めから学べる大学数学キャンパス・ゼミシリーズの「大学基礎数学」「線形代数」「微分積分」「確率統計」の4冊を2周ずつ | 100時間ぐらい |
| 2022年7月〜2023年2月 | 青本ワークブック1周目 | 100時間ぐらい |
| 2023年3月〜5月 |
青本ワークブック2周目 公式問題集 |
50時間ぐらい |
| 2023年5月〜2024年12月 | (勉強中断期間) 機械学習 や ディープラーニング などの本を読んで息抜き |
30時間ぐらい |
| 2025年1月〜3月 |
とけたろうさんの準1級講座note 青本ワークブックをサッと3周目 |
50時間ぐらい |
| 2025年4月〜6月 |
公式と例題で学ぶ統計学入門 とけたろうさんの準1級講座note2周目 青本ワークブックをサッと4周目 |
50時間ぐらい |
| 2023年7月〜8月 |
統計学入門 ガイダンス確率統計 多変量解析入門 青本ワークブック を半分まで精読 |
70時間ぐらい |
中断期間が1年半あったので、3年半かけたというよりは実質2年ですね。
Webエンジニアとして働きながらだったので、勉強しない日が多かったです。勉強した日の1日の勉強時間は30分〜2時間。
勉強内容詳細
数学の基礎固めとワークブック1周まで (2022年2月〜2023年2月)
- 2022年2月、準1級の勉強を開始
- 定番王道のワークブックを買って開くも意味不明な記号の羅列に圧倒された。総積記号の∏ やベクトル転置記号の⊤が何かも知らなかったので「なんだこの呪術書は・・・」と思った
- なので2月〜6月はワークブックに手をつける前に、初めから学べる大学数学キャンパス・ゼミシリーズの「大学基礎数学」「線形代数」「微分積分」「確率統計」の4冊を2周した
- 7月〜翌2023年2月にかけて、ワークブックを1周した
- 1周目は脳への負荷がめちゃくちゃつらくて、2時間も勉強したら疲れ切っていた。その疲労が原因と思われる熱が2回出たりもした
1度目の受験まで (2023年2月〜2023年5月)
- 2023年2月〜5月にかけて、ワークブック2周目と過去問で試験直前対策
- 理解しようとしても理解出来ず飛ばし読みする箇所が多かった。例題を解くために暗記に頼らざるを得ない部分が多かった
- 2021年以外の年のPBT過去問では6~7割の正解率だったことや、合格体験記を見ると「半年〜1年で合格した」「100〜300時間で合格した」という記事もあったので、「自分もそろそろ合格していい頃なんじゃないか・・?」と思い1度目の受験へ
1度目の不合格
- 開始10分で不合格を察した
- 何を言ってるのか分からない問題や、計算問題もどう解いていけば良いのかわからない問題が多く、「過去問やワークブック例題の表面しか理解していないお前のような者は落とす
 」という出題者からのメッセージを勝手に感じた
」という出題者からのメッセージを勝手に感じた - CBT試験では試験終了後に「優秀合格者の場合氏名を公表してよいですか?」というアンケートがある。「えっ実は合格なの・・?」という連想をさせられてからの不合格表示だったので、1度の試験で2度心を折られた
- セクション分析と合わせて振り返ると、自分の勉強法は目で読んで理屈を理解するインプットに偏っていて手を動かして計算するアウトプットの訓練が足りてないから
4. 様々の応用が15%なんだろうな、と反省した
1年半の勉強中断期間 (2023年5月〜2024年12月)
- 47点から60点までがとても遠く感じたので、モチベーションが一度切れて受験勉強を中断した
- 47点であっても結構時間を注ぎ込んで勉強したし、2級の合格に比べると学んだことはとても多いと感じていてある意味やり切った感もあった
- これまでは専門外と思い興味はあったものの避けていた機械学習系の本やディープラーニングなどの本を読むようにしたり、本業のWeb開発についてのudemyの講座を作るなど別の活動をしてた
勉強再開後、2度目の受験まで (2025年1月〜2025年3月)
-
とけたろうさんの準1級講座note が自分に合うと思い購入した
- 数式が込み入って理解出来ない所は結果だけ暗記したりスキップしながら動画教材を進めた
- 1回目の不合格の反省から、動画を眺めるだけの勉強法はしないようにした。紙とペンで手を動かしながら勉強するようにした
2度目の不合格
- 「どの分野の問題で何を問うてるのかと解法も分かる。準1級講座noteのおかげだ!」と思いながら解けて、合格の手応えがかなりあった
- 45点も失点した覚えがなかったので、不合格の瞬間は思わず天を仰いだ
- 2択まで絞れたけど迷った問題があったし、引っかけの選択肢に気づかないまま引っかかってるものがあったのかも、と反省した。勉強のやり方は変えず、また復習して「大体わかってるつもり」を「ちゃんと分かってる」に上げていく作業をしていこうと思った
3度目の受験まで
- ワークブックは飽きてきたのもあり、基礎レベルのことを問題を解きながら復習する目的で 公式と例題で学ぶ統計学入門 をやった
- 準1級講座noteも定着のためもう1周やった
3度目の不合格
- 最初の4問ぐらいが難しくて序盤でパニック気味になった
- 合格体験記によっては「時間が余って見直しが出来た」というものがあったが、その言葉を間に受けて油断してはいけないとも学んだ
- なぜならそれは十分実力がある合格者だったからであり、合格ラインギリギリの自分には適用されないと気がついた。これを条件付き期待値で表現すると
E[T|合格する実力がある] = 80, E[T|合格する実力がない] = 100 - 途中から残り時間に焦り始めて解いたので結果時間は足りたものの、精神的にゆっくり落ち着いて考える時間は無く、常にミスしやすい精神状態だったと思う
- 「これ絶対解けないといけないやつだ」っていう簡単な独立性の検定の問題を1問間違えたのも、解けてたら合格だったんだろうなあと引きずった
- なぜならそれは十分実力がある合格者だったからであり、合格ラインギリギリの自分には適用されないと気がついた。これを条件付き期待値で表現すると
- セクション分析の
4. 種々の応用が85%にまで成長したのは、準1級講座noteのおかげ。練習問題が特に自分には効果的だった。- 逆に
1. 確率と確率分布の点数が落ちてるのは準1級講座noteの範囲外(むしろ無料で動画公開してる範囲かも)でおろそかになって忘れてるのかなと振り返った。
- 逆に
4度目の受験まで
- 前回も結構解けた手応えがあったにも関わらず58点という結果だったので、何かを変えないといけないと思い、違う教材を買うことにした
- 合格体験記によく出てきてた「統計学入門」「ガイダンス確率統計」「多変量解析入門」を買ってやった
- ワークブックを改めて精読した
- 初めてワークブックを読んだ時とは全然違って読めるようになったと感じた
- 精読して、何を書いてるかの意味がわかりちゃんと読めた
- ただし15章ぐらいの所で受験日を迎えてしまい、最後まで精読しきれなかった
- 受験前の仕上げに準1級講座noteも1周流しておこうと思ったが、その時間も無かった
合格
- 4回も受験すると出題形式や時間配分に慣れた。難しい問題はスキップして後で解くようにした
- 赤本で意識して対策した
1. 確率と確率分布がめちゃ伸びた。直前期に準1級講座noteに触れられなかったため応用系の計算問題に弱くなっていた体感もあり4. 種々の応用が落ちた。誤差や運かも分からないが。 - 合格まで長かったので、めちゃ嬉しい
2025年の自分から、2022年の勉強開始時の自分に向けてアドバイスしたいこと5つ
勉強法系
アドバイス1: 青本ワークブックが難解に感じるのは、数学3Cや大学数学力の不足を理由にしたくなると思うけどそれだけじゃない。普通に統計学の内容も簡素にまとめられてしまっているのもその理由
- ワークブックに数学記号が多いけど文系だからとコンプレックスを感じすぎず、大学数学はほどほどでOK
- 大学数学キャンパス・ゼミシリーズの特に「線形代数」「微分積分」の小難しい所は深くやり込まなくても準1級合格のためなら大丈夫
- 簡単なeやlogの計算 / 重積分 / 合成関数の微分 / 固有ベクトル あたりは慣れておくべき
- 余因子展開 / 部分積分や置換積分 / マクローリン展開 / スペクトル分解 / ラグランジュの未定乗数法 あたりは雰囲気だけ知ってればOK。使いこなせなくても、解説や導出が読めずストレスを感じることはあるが合格はできる。これらに慣れてる人は準1の勉強進める上で有利そうだけど、文系出身者が準1級の合格を目指すなら優先度は下がる
- それ以上マニアックな、ε-δ論法 / ロピタルの定理 / 線形写像 / エルミート行列 などは難しい上に準1級の範囲外で基礎固めにもならないので、飛ばしてOK
- それよりも基礎固めという意味では、2級の内容を解像度高く理解することの方が大事。2級は深く理解してなくても公式に数字を当てはめるだけで77点取れてしまったが、それで2級の範囲を理解した気にならない方がよい
アドバイス2: 「青本のワークブック一冊だけを何周もやって合格」とラクしようとすると、二段飛ばしの勉強法になってしまいかえって遠回りになる
- ワークブックは良くも悪くも広い試験範囲が300ページにまとめられている。理解してる人から見ると試験範囲が1冊にまとまっている良書なんだろうだけど、理解してない人から見るとまとまってるゆえに頭に文字が入ってこない難書。1行1ページが重く進捗が出ないのも精神的につらい
- ワークブックを無理しながら読む前に赤本の「統計学入門」を挟むと良い。この本はネット上では2級対策とも言われていて「入門」というタイトルからもバイアスがかかりパッと見2級の内容に見えるが、実は準1級と考えてよい。ワークブックの1章〜12章の100ページ分を200ページで解説してるって感じなので、こっちの方が読みやすい。
- 赤本の次は緑色の「多変量解析入門」も挟むと良い。これはワークブック後半部分の、重回帰分析や多変量解析の章に対応している。赤本の復習にもなる。
- この2冊をやった後で青本のワークブックに取り組む方が、無理の少ない1段ずつのステップアップになり理解がスムーズのはず。試験に必要な手を動かして具体的な計算する力も身につきやすい。
具体的な内容系 (大事なことなのに初回受験時には知らなかった常識3つ...)
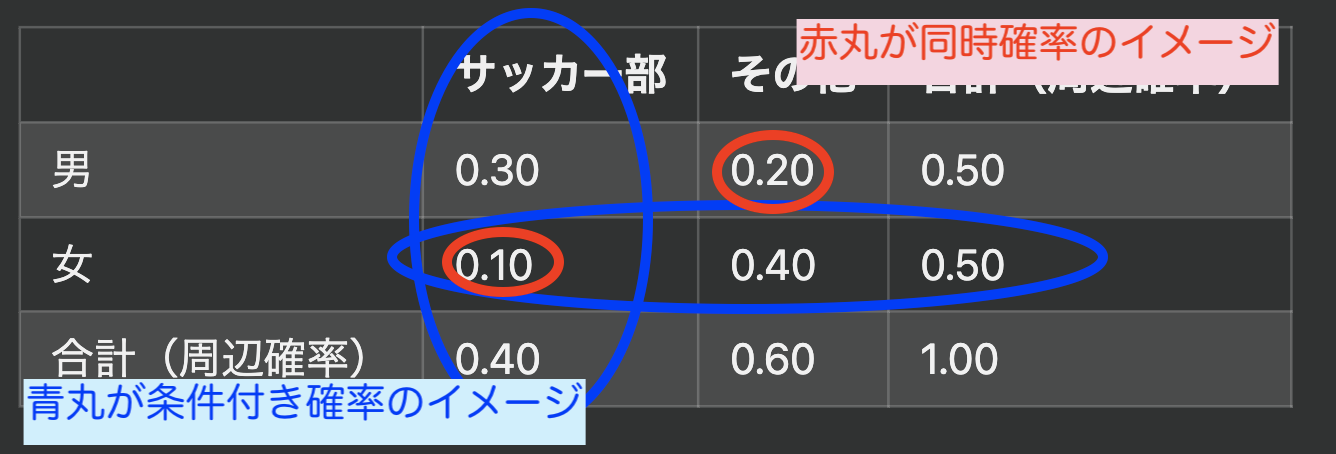
アドバイス3:ワークブックの7,8ページ目にサラっと書いてる 同時確率 周辺確率 条件付き確率 の理解はとても大事
| サッカー部 | その他 | 合計(周辺確率) | |
|---|---|---|---|
| 男 | 0.30 | 0.20 | 0.50 |
| 女 | 0.10 | 0.40 | 0.50 |
| 合計(周辺確率) | 0.40 | 0.60 | 1.00 |
みたいな例があるとしたら、↓のイメージに慣れること
- 最尤法が理解しやすくなり、∏や積分記号へのアレルギーが結構減る
アドバイス4: 確率密度関数 = 積分したら1 ということを知っておかないといけない
- 確率は全部足したら100%っていう当たり前のことを分かってなかった
- これを知ってると
-
https://toketarou.com/poisson/#toc3 にあるポアソン分布の確率密度関数が覚えやすくなる(
Exp(x)のマクローリン展開と紐づけて覚えれるようになる ) -
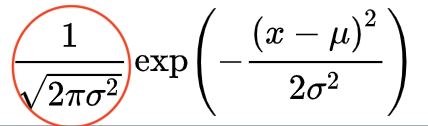
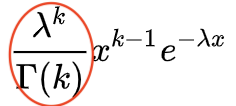
↑こういうウエッてなる確率密度関数をみた時、「赤丸部分はただ1にしてあげるため基準化定数という脇役で、その右側の部分が確率密度関数の主役」という理解になり抵抗感が減るようになる -
ワークブック14章のマルコフ連鎖の傘の問題の連立方程式を立てる時にも使う
-
などなど各所での理解を支える。
アドバイス5: 中心極限定理について
よくある上記図のように「標本数nが増えると分散が減って真ん中に集まっていく」というイメージでずっといた。2級ではこのレベルの理解でごまかせたが準1級だとごまかしきれない感じがしていた。
そんな時、赤本の8章の162ページにある以下の説明が自分的に一番しっくり来た
ワークブックの例題7.1や9.1を解く時にこの説明とセットで確認しながら解くと理解が深まって安心できる。
また2標本問題のプールした分散を求める時も公式の暗記ではない理解ができるようになる。
これから
機械学習系の知識もあるWebエンジニアとして生きていきたい。
2級合格時ではきちんと読めなかったであろう ゼロから作るDeep Learning 5 や ビジネス課題を解決する技術 といった技術書がなんとか読めるようになり楽しい。