線形回帰について現時点で私が理解していることと、その過程で書いたPythonのコードをまとめます。数学はガバガバですがご了承ください。
回帰分析
回帰分析とは、原因となったデータと結果となったデータを分析し、その二つのデータの関係性を導き出すための手法です。線形と非線形に分けることができます。
線形回帰
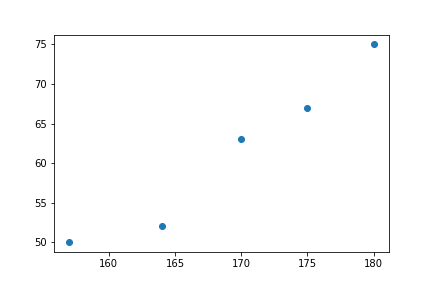
身長と体重の二つの変数からなるデータを考えてみましょう。以下のデータがあったとします。
| 身長 | 体重 |
|---|---|
| 170 | 63 |
| 175 | 67 |
| 164 | 52 |
| 157 | 50 |
| 180 | 75 |
これを散布図で表してみます
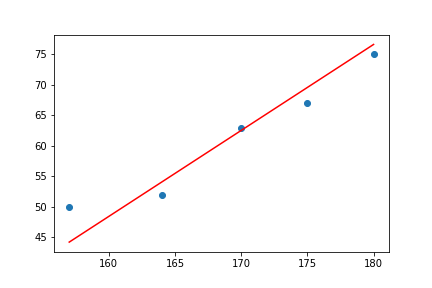
この図に対して、いい感じな直線を引いてみましょう。
できました。
このいい感じな直線を計算で求めるのが線形回帰となります。
非線形回帰
本稿で扱うのは線形回帰ですが、非線形も軽く触れておきます。
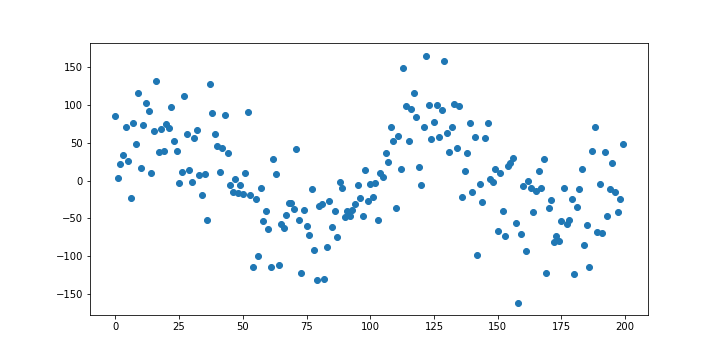
先ほどはいい感じな直線が引けそうなデータでしたが、その様なデータばかりではありません。例えば下の図。
この様なデータの場合、直線ではなく曲線を引くことを考えます。
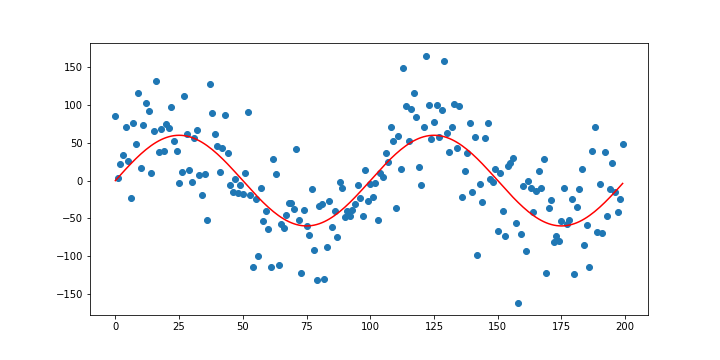
こんな感じです。非線形回帰では、いい感じの曲線を計算で求めます。
(画像は多分$\sin x$なので非線形と言えますが、例えば適当な$m$次の項までの線型結合によって求められていた場合などはこれは線形回帰になります。コメントをいただいていたのに長らく放置していてすいません。)
単回帰と重回帰
上で挙げた二つの例はいずれも単回帰です。単回帰とは、原因となるデータが一次元の場合を指します。上の線形回帰の例では、「身長」という一種類のデータだけで体重を予測していたので、単回帰となります。
一方で、原因となるデータが多次元の場合は重回帰となります。例を挙げると、身長の他に「睡眠時間」「摂取カロリー」「運動量」などが加わった多次元のデータから体重を予測するなどです。
それでは実際に線形回帰をやっていきましょう
単回帰
まずは単回帰からです。最小二乗法を使っていい感じの直線を求めていきます。
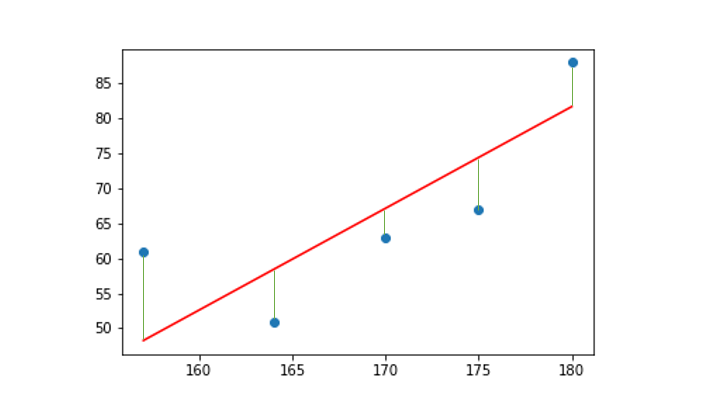
最小二乗法では、線を引いた時、その線とデータの差の二乗和が最小になる様に線を引きます。図で見てみましょう。
この緑の線の長さの和が最小になる直線を求めようと言うことですね。
では計算していきます。
求めたい直線を
$f(k) = ak + b$
と置きます。 また、原因となったデータ$x$と、結果となったデータ$y$を
$x = (x_1 \ x_2\ \cdots \ x_n)$
$y = (y_1 \ y_2\ \cdots \ y_n)$
とします。因みに、原因となったデータを説明変数、結果となったデータを目的変数と呼びます。以下、本稿でもこの表現を用います。
次に、最小化したい関数$E$を以下の様に定義します。これが直線と点の距離の二乗和です。
E = \sum_{i=1}^{n} \big(f(x_i) - y_i\big)^2 = \sum_{i=1}^{n} \big(ax_i + b - y_i\big)^2
そしてこの$E$を最小にする$a$と$b$を求めます。$E$は$a$と$b$の二次関数で、二つの係数はいずれも正なので、偏微分をして傾きが0になる値を探せばいいですね。
\begin{align}
\frac{\partial E}{\partial a} &= 2\sum_{i=1}^{n} x_i \big(ax_i + b - y_i\big)=0 \, \cdots ① \, \\
\frac{\partial E}{\partial b} &= 2\sum_{i=1}^{n} \big(ax_i + b - y_i\big)=0 \, \cdots \, ②
\end{align}
この連立方程式を解いていきます。まず両辺を2で割り、展開してから$y_i$の項を移行します。
\begin{align}
a\sum_{i=1}^{n}x_i^2 + \sum_{i=1}^{n}bx_i &= \sum_{i=1}^{n}x_iy_i \ \cdots ① \\
a\sum_{i=1}^{n}x_i + bn &= \sum_{i=1}^{n}y_i \ \cdots ②
\end{align}
②より、$b$が求まります。
b = -a\frac{\sum_{i=1}^{n}x_i}{n} + \frac{\sum_{i=1}^{n}y_i}{n} = -a\bar{x} + \bar{y}
$b$を$x$と$y$の平均で表すことができました。これを①に代入しして色々いじります。
\begin{align}
a\sum_{i=1}^{n}x_i^2 + \sum_{i=1}^{n}(-a\bar{x} + \bar{y})x_i &= \sum_{i=1}^{n}x_iy_i \\
a\sum_{i=1}^{n}x_i^2 - a\bar{x}\sum_{i=1}^{n}x_i &= \sum_{i=1}^{n}x_iy_i - \bar{y}\sum_{i=1}^{n}x_i\\
\end{align}
両辺をnで割り、$a$を求めます。
\begin{align}
a(\bar{x^2}-\bar{x}^2) &= \bar{xy} - \bar{x}\bar{y} \\
a &= \frac{\bar{xy} - \bar{x}\bar{y}}{\bar{x^2}-\bar{x}^2} = \frac{\sigma_{xy}}{\sigma_x^2}
\end{align}
$a$を$xy$の共分散と$x$の分散で表すことができました。まとめるとこうなります。
\begin{align}
a &= \frac{\sigma_{xy}}{\sigma_x^2} \\
b &= -a\bar{x} + \bar{y}
\end{align}
これを $f(x) = ax + b$ に代入すれば完成ですね。
Pythonで実装
以上の内容をPythonで実装していきましょう
import numpy as np
import matplotlib.pyplot as plt
class simple_linear:
# 回帰係数と切片の計算
def fit(self, X, y):
self.X = X # 説明変数
self.y = y # 目的変数
self.a = np.cov(X, y)[0, 1] / np.var(X) # 回帰係数
self.b = -self.a * X.mean() + y.mean() # 切片
# 予測
def predict(self, X):
return self.a*X + self.b
# プロット
def plot(self):
plt.scatter(self.X, self.y)
Xlim = np.array([self.X.min(), self.X.max()])
plt.plot(Xlim, self.predict(Xlim), color='Red')
単回帰を行うクラスです。メソッドはscikit-learnに倣って書きました。単回帰ということでplot()というメソッドも書いてみました。クラスについてよく分からない方は中の関数だけ見て下さい。
fit()で先ほどの計算が行なわれます。np.var()で分散、np.cov()で共分散が得られます。また、np.cov()は共分散行列というものを返すメソッドで、(x, y)を引数に入れると以下の様な行列(ndarray)が返されます。
\begin{pmatrix}
\sigma_{xx} & \sigma_{xy} \\
\sigma_{yx} & \sigma_{yy}
\end{pmatrix}
$\sigma_{xx}$、$\sigma_{yy}$はxとyの分散です。欲しいのは共分散$\sigma_{xy}$なので、インデックスとして[0,1]を指定しています([1,0]でも可)。
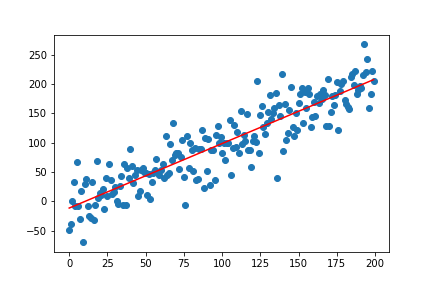
実行してみるとこんな感じです。
# 適当なデータ生成
X = np.arange(200)
y = X + np.random.randn(200)*30
reg_simple = simple_linear()
reg_simple.fit(X, y)
reg_simple.plot()
重回帰
今度は重回帰をしましょう。単回帰と同じ様に計算を進めてもできると思いますが、計算が煩雑になるため、ある前提を考えます。それは、説明変数と目的変数が全て標準化されているというものです。標準化とは、平均が0、標準偏差が1になる様にデータをスケーリングすることです。具体的には、全データから平均値を引き、標準偏差で割ることで得られます。こうすることで切片の値を0にできるため、計算がし易くなります。
それでは計算をしていきましょう。二つの変数が標準化されていると言う前提の元で進めていきます。
まず求めたい関数を、
$f(k_1, k_2 \cdots k_m) = a_1k_1 + a_2k_2 + \cdots + a_mk_m$
と置きます。$m$は説明変数の次元数です。重回帰なので、説明変数とそれぞれの係数は多次元になります。
また、説明変数$X$、目的変数$y$を
X = \begin{pmatrix}
x_{11} & x_{12} & \cdots & x_{1m} \\
x_{21} & x_{22} & \cdots & x_{2m} \\
\vdots & \vdots & \ddots & \vdots \\
x_{n1} & x_{n2} & \cdots & x_{nm} \\
\end{pmatrix} \\
y = \begin{pmatrix}
y_1 \\
y_2 \\
\vdots \\
y_n
\end{pmatrix}
とし、$X_1 \ X_2 \ \cdots \ X_n$ を
X_1 = \begin{pmatrix}
x_{11} \\
x_{12} \\
\vdots \\
x_{1m} \\
\end{pmatrix}\
X_2 = \begin{pmatrix}
x_{21} \\
x_{22} \\
\vdots \\
x_{2m} \\
\end{pmatrix}\
\cdots \
X_n = \begin{pmatrix}
x_{n1} \\
x_{n2} \\
\vdots \\
x_{nm} \\
\end{pmatrix}\
とします。$X$は、データ数$n$ $\times$ 次元数$m$ の説明変数全体の行列で、$X_i$ は、ある目的変数$y_i$に対する説明変数を表します。
次に、最小化したい関数$E$を以下の様に定義します。
E = \sum_{i=1}^{n}(f(X_i) - y_i)^2 = \sum_{i=1}^{n}(a_1x_{i1} + a_2x_{i2} + \cdots + a_mx_{im}- y_i)^2
そしてこの$E$を最小にする $a_1 \ a_2 \cdots \ a_m$ を求めます。$E$は各回帰係数 $a_1 \ a_2 \cdots \ a_m$ の二次関数でそれらの係数はいずれも正なので、単回帰同様、偏微分をして傾きが0になる値を探します。
\begin{align}
\frac{\partial E}{\partial a_1} &= 2\sum_{i=1}^{n}x_{i1}(a_1x_{i1} + a_2x_{i2} + \cdots + a_mx_{im}- y_i) = 0 \\
\frac{\partial E}{\partial a_2} &= 2\sum_{i=1}^{n}x_{i2}(a_1x_{i1} + a_2x_{i2} + \cdots + a_mx_{im}- y_i) = 0 \\
\vdots \\
\frac{\partial E}{\partial a_m} &= 2\sum_{i=1}^{n}x_{im}(a_1x_{i1} + a_2x_{i2} + \cdots + a_mx_{im}- y_i) = 0
\end{align}
この連立方程式を解いていきます。こちらも単回帰同様、まず両辺を2で割り、展開してから$y_i$の項を移行します。
\begin{align}
a_1\sum_{i=1}^{n}x_{i1}x_{i1} + a_2\sum_{i=1}^{n}x_{i1}x_{i2} + \cdots + a_m\sum_{i=1}^{n}x_{i1}x_{im} &= \sum_{i=1}^{n}x_{i1}y_i \\
a_1\sum_{i=1}^{n}x_{i2}x_{i1} + a_2\sum_{i=1}^{n}x_{i2}x_{i2} + \cdots + a_m\sum_{i=1}^{n}x_{i2}x_{im} &= \sum_{i=1}^{n}x_{i2}y_i \\
\vdots \\
a_1\sum_{i=1}^{n}x_{im}x_{i1} + a_2\sum_{i=1}^{n}x_{im}x_{i2} + \cdots + a_m\sum_{i=1}^{n}x_{im}x_{im} &= \sum_{i=1}^{n}x_{im}y_i
\end{align}
できました。ここから単回帰と手順が異なります。
この式を、行列に置き換える作業を行います。まずは、これらを単純な$m$行1列の行列にしてみましょう。
\begin{pmatrix}
a_1\sum_{i=1}^{n}x_{i1}x_{i1} + a_2\sum_{i=1}^{n}x_{i1}x_{i2} + \cdots + a_m\sum_{i=1}^{n}x_{i1}x_{im} \\
a_1\sum_{i=1}^{n}x_{i2}x_{i1} + a_2\sum_{i=1}^{n}x_{i2}x_{i2} + \cdots + a_m\sum_{i=1}^{n}x_{i2}x_{im} \\
\vdots \\
a_1\sum_{i=1}^{n}x_{im}x_{i1} + a_2\sum_{i=1}^{n}x_{im}x_{i2} + \cdots + a_m\sum_{i=1}^{n}x_{im}x_{im}
\end{pmatrix}
=
\begin{pmatrix}
\sum_{i=1}^{n}x_{i1}y_i \\
\sum_{i=1}^{n}x_{i2}y_i \\
\vdots \\
\sum_{i=1}^{n}x_{im}y_i
\end{pmatrix}
次に $a_1 \ a_2 \ \cdots \ a_m$ を縦に並べた以下の行列$a$を考えます。
a = \begin{pmatrix}
a_1 \\
a_2 \\
\vdots \\
a_m
\end{pmatrix}
この行列を使って、左辺を表してみましょう。
\begin{pmatrix}
\sum_{i=1}^{n}x_{i1}x_{i1} & \sum_{i=1}^{n}x_{i1}x_{i2} & \cdots & \sum_{i=1}^{n}x_{i1}x_{im} \\
\sum_{i=1}^{n}x_{i2}x_{i1} & \sum_{i=1}^{n}x_{i2}x_{i2} & \cdots & \sum_{i=1}^{n}x_{i2}x_{im} \\
\vdots & \vdots & \ddots & \vdots \\
\sum_{i=1}^{n}x_{im}x_{i1} & \sum_{i=1}^{n}x_{im}x_{i2} & \cdots & \sum_{i=1}^{n}x_{im}x_{im}
\end{pmatrix}
\begin{pmatrix}
a_1 \\
a_2 \\
\vdots \\
a_m
\end{pmatrix}
=
\begin{pmatrix}
\sum_{i=1}^{n}x_{i1}y_i \\
\sum_{i=1}^{n}x_{i2}y_i \\
\vdots \\
\sum_{i=1}^{n}x_{im}y_i
\end{pmatrix}
こうですね。元の行列から$a$を外に出したイメージでしょうか。このまま、他の行列を$x$と$y$の比較的単純な行列で表すことができれば、$a$ を求めることができそうですね。やってみましょう。
一番左の行列は、$X^T$と$X$の積になっています。$X^T$は、$X$の転置行列(行と列が逆になった行列)を表します。
\begin{pmatrix}
\sum_{i=1}^{n}x_{i1}x_{i1} & \sum_{i=1}^{n}x_{i1}x_{i2} & \cdots & \sum_{i=1}^{n}x_{i1}x_{im} \\
\sum_{i=1}^{n}x_{i2}x_{i1} & \sum_{i=1}^{n}x_{i2}x_{i2} & \cdots & \sum_{i=1}^{n}x_{i2}x_{im} \\
\vdots & \vdots & \ddots & \vdots \\
\sum_{i=1}^{n}x_{im}x_{i1} & \sum_{i=1}^{n}x_{im}x_{i2} & \cdots & \sum_{i=1}^{n}x_{im}x_{im}
\end{pmatrix}
=
X^TX
右辺の行列は、$X^T$と$y$の積で表せますね。
\begin{pmatrix}
\sum_{i=1}^{n}x_{i1}y_i \\
\sum_{i=1}^{n}x_{i2}y_i \\
\vdots \\
\sum_{i=1}^{n}x_{im}y_i
\end{pmatrix}
=
X^Ty
まとめてみましょう
X^TXa = X^Ty
綺麗にまとまりました。
$a=$ 〜 の形にしたいので、両辺に$(X^TX)^{-1}$を左からかけ、左辺を$a$にしましょう。
a = (X^TX)^{-1}X^Ty
できました。 $(X^TX)^{-1}$は$X^TX$の**逆行列**を表します。逆行列とは、積をとった時に**単位行列**となる行列で、単位行列とは、積をとった時にどの行列に対しても変化を与えない行列を指します。行列において、逆行列は「逆数」、単位行列は「1」の様な働きします。
Pythonで実装
では、ここまでをPythonで実装してみましょう。
import numpy as np
from scipy.stats import zscore # 標準化用の関数
class linear_sta:
def fit(self, X, y):
# 標準偏差と平均の保存
self.X_mean = np.array(X.mean(axis=0)) # 平均
self.X_std = np.array(X.std(axis=0)) # 標準偏差
self.y_mean = y.mean()
self.y_std = y.std()
# 標準化して行列に変換
self.X = np.matrix(zscore(X, axis=0))
self.XT = np.matrix(zscore(X.T, axis=1))
self.y = np.matrix(zscore(np.array(y)).reshape(-1,1))
# 回帰係数
XT_X_inverse = np.linalg.pinv(self.XT * self.X) # XTとXの積の逆行列
XT_y = self.XT * self.y # XTとyの積
self.a = np.array(XT_X_inverse * XT_y).ravel() # 積をとって平坦化
# 予測
def predict(self, X):
sta_X = np.array((X - self.X_mean) / self.X_std) # fitで入れた説明変数でスケーリング
return np.dot(sta_X, self.a) * self.y_std + self.y_mean # 回帰係数との内積をとって標準化した分を戻す
例によってfit()で計算が行われます。一つ一つ見ていきましょう。
# 標準偏差と平均の保存
self.X_mean = np.array(X.mean(axis=0)) # 平均
self.X_std = np.array(X.std(axis=0)) # 標準偏差
self.y_mean = y.mean()
self.y_std = y.std()
平均値と標準偏差を変数に格納しています。Xとyが標準化されているという前提のもとで回帰係数($a$)を求めたため、予測を行う際に、入力データをこのデータに基づいてスケーリングする必要があるからです。また、axisのデフォルト値はNoneなので、「列ごとに」を意味するaxis=0を指定しています。
# 標準化して行列に変換
self.X = np.matrix(zscore(X, axis=0))
self.XT = np.matrix(zscore(X.T, axis=1))
self.y = np.matrix(zscore(np.array(y)).reshape(-1,1))
標準化したデータを行列として変数に代入しています。zscore()で標準化、np.matrixで行列に変換しています。np.array()でndarrayに変換しても同じ演算ができますが、行列として扱う場合はmatrixの方が便利です。.Tは転置行列、reshape(-1,1)は 1 $\times$ $n$ の配列を $n$ $\times$ $1$ に変換して返しています。
# 回帰係数
XT_X_inverse = np.linalg.pinv(self.XT * self.X) # XTとXの積の逆行列
XT_y = self.XT * self.y # XTとyの積
self.a = np.array(XT_X_inverse * XT_y).ravel() # 積をとって平坦化
定義した行列を使って回帰係数を求めています。np.linalg.pinv()は逆行列を返します。np.linalg.inv()または**-1でも逆行列が求められますが、元の行列が正則行列でない(逆行列を持たない)ときにエラーを吐いてしまいます。np.linalg.pinv()では擬似的な逆行列を生成してエラーを回避できるため、採用しています。
predict()も見ていきましょう
# 予測
def predict(self, X):
sta_X = np.array((X - self.X_mean) / self.X_std) # fitで入れた説明変数でスケーリング
return np.dot(sta_X, self.a) * self.y_std + self.y_mean # 回帰係数との内積をとって標準化した分を戻す
まず、入力データからfit()で定義した平均を引き、標準偏差で割ることでスケーリングをしています。そしてnp.dot()で回帰係数との内積をとり、目的変数の標準偏差をかけて平均を足すことで、スケーリングした分を元に戻しています。
予測してみる
実際に予測してみましょう。こちらのデータセットを使います。コンクリートの成分から圧縮強度ってやつを求めてみましょう。
import pandas as pd
from sklearn.model_selection import train_test_split
data_path = 'https://archive.ics.uci.edu/ml/machine-learning-databases/concrete/compressive/Concrete_Data.xls'
df = pd.read_excel(data_path) # データセット読み込み
y_columns = 'Concrete compressive strength(MPa, megapascals) ' # 圧縮強度
X = df.drop(columns=y_columns) # 説明変数
y = df[y_columns] # 目的変数
X_train, X_test, y_train, y_test = train_test_split(X, y) # 訓練データとテストデータに分割
linear_s = linear_sta() # インスタンス生成
linear_s.fit(X_train, y_train) # 回帰係数の計算
pre_X = X_test.iloc[:3] # テストデータの上三つ
pre_y = np.array(y_test[:3]) # その正解
print(f'予測値: {linear_s.predict(pre_X)}')
print(f'正解: {pre_y}')
実行するとこうなりました。
予測値: [40.02633476 25.91338266 31.51666727]
正解: [40.8686899 19.41564416 38.56239268]
まあまあですかね? train_test_split()がランダムなので、試行毎に結果は変わります。
回帰係数を直す
今求めた回帰係数を見てみましょう。
print(linear_s.a)
するとこうなります。
[ 0.77131819 0.55916812 0.37295602 -0.15677616 0.10616719 0.09854152
0.11658664 0.43031912]
0付近に固まっていますが、これはデータを標準化したためです。上でやった通りこれでも予測はできますが、回帰係数は直線の傾きを表しており、各説明変数が目的変数に与えている影響として見ることができるため、可能なら元のスケールで表したいですね。
predict()の中を数式で表してみましょう。入力データを縦に並べた行列を$k$、$X$の列ごとの標準偏差・平均を縦に並べた行列をそれぞれ $\sigma_x, \bar{X}$ とすると、出力を以下の様に表せます。
(k - \bar{X}) \oslash \sigma_x ・ a \times \sigma_y + \bar{y}
$\oslash$はアダマール積の記号です。行列の格要素ごとに除算を行います。乗算の場合は$\otimes%$を使います。
上の式を、$k \ ・A + B$ の形に変形します。
\begin{align}
(k - \bar{X}) \ ・ \frac{a}{\sigma_x}\sigma_y + \bar{y} \\
k \ ・ \frac{a}{\sigma_x}\sigma_y - \bar{X} \ ・ \frac{a}{\sigma_x}\sigma_y + \bar{y}
\end{align}
こうなりました。これで、元の回帰係数 $A = \frac{a}{\sigma_x}\sigma_y$、切片 $B = - \bar{X} \ ・ A + \bar{y}$ が求まりました。やったぜ。
Pythonで実装
以上の内容を、Pythonにも反映させましょう。
class Linear:
def fit(self, X, y):
# 標準偏差と平均
self.X_mean = np.array(X.mean(axis=0))
self.X_std = np.array(X.std(axis=0))
# 標準化して行列に変換
self.X = np.matrix(zscore(X, axis=0))
self.XT = np.matrix(zscore(X.T, axis=1))
self.y = np.matrix(zscore(np.array(y)).reshape(-1,1))
# 回帰係数と切片
XT_X_inverse = np.linalg.pinv(self.XT * self.X) # XTとXの積の逆行列
XT_y = self.XT * self.y # XTとyの積
self.A = np.array(XT_X_inverse * XT_y).ravel() / self.X_std * y.std()
self.B = -np.dot(self.b, self.X_mean) + y.mean()
# 予測
def predict(self, X):
return np.dot(X, self.A) + self.B
predict() がシンプルになりましたね。予測もしてみましょう。
linear = Linear()
linear.fit(X_train, y_train)
print(f'予測値: {linear_s.predict(pre_X)}')
予測値: [40.02633476 25.91338266 31.51666727]
しっかり同じ値になりました。
おまけ
scikit-learnを使って先ほど求めた回帰係数が正しいか確かめてみましょう。
from sklearn import linear_model
reg = linear_model.LinearRegression()
reg.fit(X_train, y_train)
print('自作')
print(linear.A)
print(linear.B)
print('----------------------')
print('sklearn')
print(reg.coef_)
print(reg.intercept_)
結果
自作
[ 0.12291481 0.10560904 0.09741413 -0.12366291 0.29375934 0.02143313
0.02399962 0.11264403]
-35.85204847096638
----------------------
sklearn
[ 0.12291481 0.10560904 0.09741413 -0.12366291 0.29375934 0.02143313
0.02399962 0.11264403]
-35.852048470969976
ちゃんと一致していました
これで終わります。ありがとうございました!
参考