久しぶりにpandasなどデータ分析の学び直しをやりたかったので、せっかくなら一昨日終わったばっかりのM-1グランプリのデータでやってみたいと思います。
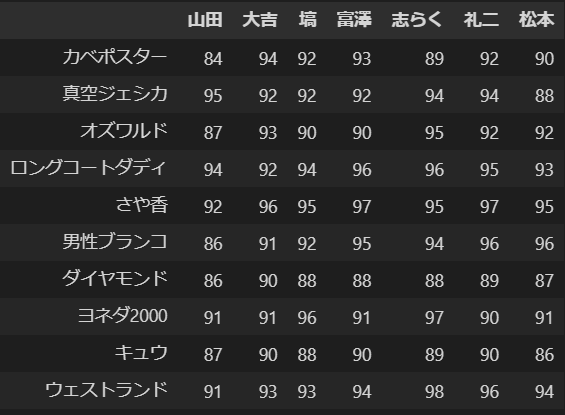
まずは採点結果をcsvファイルに保存(ここでは、まだ合計は入れないでおく)
,山田,大吉,塙,富澤,志らく,礼二,松本
カベポスター,84,94,92,93,89,92,90
真空ジェシカ,95,92,92,92,94,94,88
オズワルド,87,93,90,90,95,92,92
ロングコートダディ,94,92,94,96,96,95,93
さや香,92,96,95,97,95,97,95
男性ブランコ,86,91,92,95,94,96,96
ダイヤモンド,86,90,88,88,88,89,87
ヨネダ2000,91,91,96,91,97,90,91
キュウ,87,90,88,90,89,90,86
ウェストランド,91,93,93,94,98,96,94
まずはpandasをインポートして上記のcsvファイルを読み込み
import pandas as pd
score_df = pd.read_csv("M-1_2022_score.csv", index_col=0)
score_df
出力結果
手っ取り早く、基本統計情報を見るにはdescribe()を使います。
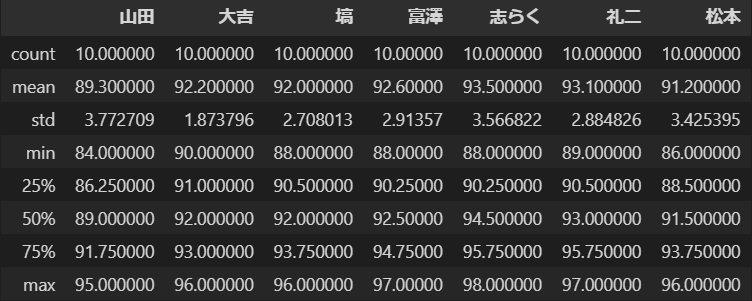
score_df.describe()
出力結果
まず、ここで注目するのはstd:標準偏差の行です。この値が高い審査員ほど採点のばらつきの幅が大きくなるので、最終結果に与える影響が大きくなります。これを見ると山田、志らく、松本が高く、大吉は低いですね。
箱ひげ図でも表示してみましょう。
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'MS Gothic'
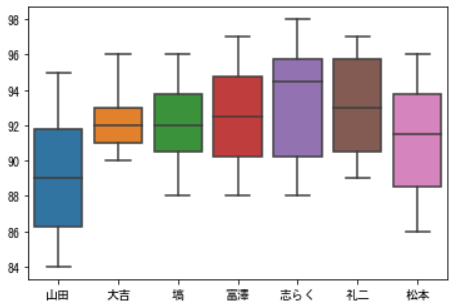
sns.boxplot(data=score_df)
出力結果
やっぱり、山田邦子は幅が大きく、少しだけ基準が低いですね。
次は、審査結果が近い人と遠い人がいそうなので、PCAで次元消滅させて可視化してみましょう。
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
features = pca.fit_transform(score_df.T)
X = features[:, 0]
Y = features[:, 1]
plt.scatter(X, Y)
for i,(x, y) in enumerate(zip(X, Y)):
plt.annotate(score_df.T.index[i],(x, y))
plt.xlabel("PC1")
plt.ylabel("PC2")
plt.grid()
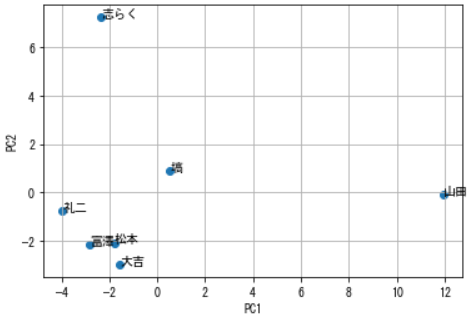
plt.show()
出力結果
確かに、なんとなく大吉、富澤、礼二、松本は正統派が好きな印象で、志らくはヨネダ2000とか個性派を好み、塙はその中間って感じしますね。そして独特な感性で採点する山田邦子。
最後に
ウェストランドのネタで「ネタの分析とかしてくるウザいお笑いファンいるか~」って言ってたけど、ワイの事やった。