この記事はPSE Core Program 2024の一環として作成されました。
この記事を含む、ゼロ知識証明技術に関する学習内容は以下のリンクで公開されています。
STARKs
以下のvitalik氏の記事を自分なりに解釈したものとなっています。
vitalik氏の記事から拝借している図もあります。ご了承ください。
- https://vitalik.eth.limo/general/2017/11/09/starks_part_1.html
- https://vitalik.eth.limo/general/2017/11/22/starks_part_2.html
概要
zkSNARKsは検証可能な計算やプライバシー保護型暗号通貨など、さまざまな用途に使用できる汎用の簡潔なゼロ知識証明技術である。zkSTARKsの「T」は透明性(Transparent)を意味し、zkSNARKsの課題であったTrusted Setupへの依存を解消している。また、楕円曲線やペアリング、KEAを必要とせず、ハッシュと情報理論に基づいている。これにより、量子コンピュータを持つ攻撃者に対しても安全である。
STARKs, Part I: Proofs with Polynomials
「ある多項式$P(x)$を知っている」ことを証明したいとする。ここでは例として$P(x)$と$x$は以下の性質を満たすと仮定する。
(0 \leq P(x) \leq 9), \{x \in \mathbb{N} \mid 1 \leq x \leq 10^6\}
単純な証明を考えると、100万点全てで$(0 \leq P(x) \leq 9)$を確認する方法が考えられる。しかし、これは大変なのでランダムな点で検証する方法が考えられる。しかしこれもまた、サンプリングしたランダムな点において偶然$P(x)$と一致していた$P(x)'$が検証を通過してしまうという問題がある。
問題の変換
まず、制約チェック多項式$C(x)$を導入する。$C(x)$は以下の性質を満たす。
\displaylines{
\begin{align}
&C(x) = (x-1)(x-2) \cdots (x-9) \\
&C(x) =
\begin{cases}
0 & \text{if } 0 \leq P(x) \leq 9 \\
\neq 0 & \text{if } P(x) < 0 \text{ or } P(x) > 9
\end{cases}
\\
\end{align}
}
ここで、「多項式$P(x)$を知っている」という問題は「$C(P(x))=0$なる$P(x)$を知っている」という問題に変換される。
次に、$C(P(x))$は$(1 \leq x \leq 10^6)$を根に持つため、$C(P(x))$は多項式$Z(x)=(x-1)(x-2)\cdots (x-10^6)$で割り切れるという事実を用いると、
「$C(P(x))=0$なる$P(x)$を知っている」という問題は、「$C(P(x)) = Z(x)D(x)$なる$P(x)$と$D(x)$を知っている」という問題に変換される。$D(x)$は$C(P(x))$を$Z(x)$で多項式除算すれば求まる。
証明プロセス
問題の変換によって、以下のように証明プロセスを構築できる。
- 証明者は$(1 \leq x \leq 10^9)$における$P(x)$と$D(x)$の値をマークルツリーにして、マークルルートを検証者にコミットする
- 検証者は16個の値$u \in (1 \leq x \leq 10^9)$を選び証明者に送る
- 証明者は$u$における$P(x)$と$D(x)$のマークルパスを検証者に送る
- 検証者はマークルパスからマークルルートを構成できること、$C(P(x)) = Z(x)D(x)$が$u$において成り立つことを検証する
- 検証が通れば、証明者は$P(x)$を知っていることを証明できる
図で表すと以下の様になる。
更に、証明者はマークルルートをエントロピー源として$u$を生成することで、このプロセスを非対話式にできる。これは、マークルルートを任意の値にすることが困難であるために安全に機能する。
脆弱性1
仮に攻撃者が$C(P(x)’) \neq Z(x)D(x)’$なる$P(x), D(x)$と次数が同じ多項式$P(x)', D(x)'$を偽造した場合を考える。
まず、数学的事実としてN次多項式同士の交点はたかだかN点しかない。$C(P(x)’)$と$Z(x)D(x)’$は1000万次多項式なので、交点はたかだか1000万点しかない。つまり、偶然$C(P(x)’) = Z(x)D(x)’$が成り立つ確率は最大でも$10^7 / 10^9 = 0.01$となる。証明プロセスでは16個の値$u$を使用しているので,偶然検証を通過する確率は$10^{-32}$となる。
今回は$P(x)', D(x)'$の次数が$P(x), D(x)$と同じ場合を考えたため安全そうに見える。しかし、仮に$P(x)', D(x)'$の次数が非常に大きい場合を考えると交点も非常に多くなるため、偶然$C(P(x)’) = Z(x)D(x)’$が成り立つ確率は$0.01$よりも遥かに大きくなってしまう。
つまり、この攻撃を防ぐためには証明者が提供する$P(x)$と$D(x)$の次数に上限を設ける必要がある。
脆弱性2
次に、攻撃者が以下の様に$P(x)$と$D(x)$を偽造した場合を考える。
- $P(x)$の代わりに適当な値$p$を使う
- $D(x)$の代わりに$d=C(p)/Z(x)$を使う
この場合、$C(p)=Z(x)d$は常に成り立つため検証を通過する。
つまり、この攻撃を防ぐためには証明者が提供する点の集合が、ある多項式上に存在することを検証する必要がある。
解決策
これらの脆弱性に対応するため、low-degree testingの一種であるFRIを導入する。これによって、証明者から提供された点の集合が確かにある次数未満の多項式上にあることを検証することで、上記の攻撃手法を防ぐことができる。
STARKs, Part II: Thank Goodness It's FRI-day
証明者が提供した点の集合について、それら全てが次数$D$未満の同じ多項式上にあると主張することを考える。
仮に$p$割の点が多項式上に無い場合、この主張は$D+k$回の(検証者側の)クエリで$(1-p)^k$の確率で検証を通過する。(ラグランジュ補間を使えば$D+1$個の点から$D$次多項式を作れるため)
このままでも良いが、$D$が大きい場合は大変なので、以下のテクニックを使って証明者・検証者の計算量を削減していく。
二変数関数
10億個の点が次数100万未満の多項式$f(x)$上にあるとする。
まず、$f(x)=g(x, x^{1000})$を満たすような二変数関数$g(x, y)$を見つける$(y=x^{1000})$。見つけ方は簡単で、$f(x)$の$k$次の項を以下の様に変換すればよい。
x^k \to x^{k \bmod 1000}y^{floor(k / 1000)}
例えば$1744x^{185423}$という項は以下のように変換される。
1744x^{185423} \to 1744x^{423}y^{185}
この変換を用いると、次に記すように$D+k$回のクエリ以下で検証を行う事ができる。
証明プロセス
二変数関数を用いて以下のように証明プロセスを構築できる。
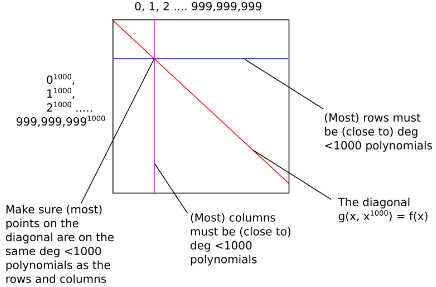
- 証明者は$g(x, y)$を計算して以下の正方形を作成し、10億×10億個の値をツリーにしてマークルルートをコミットする(正方形の対角線は$f(x) = g(x, x^{1000})$の値を意味する)
- 検証者は行と列を数十個指定して、各行/列に対して$1000 + k$個の点を要求する (このうち一つは対角線上の点)
- 証明者は指定された点における$g(x, y)$の値とマークルパスを提出する
- 検証者はマークルパスが正しいこと、各行/列の点が次数<1000の多項式上にあることを検証する
- 検証が通れば、証明者は提供した点の集合がある次数未満の多項式上にあることを証明できる
$f(x)$は次数100万未満の多項式であったが、行と列を指定($x$or$y$を固定)することで$f(x) = g(x, y)$を次数1000未満の多項式にすることができた。
例として30行, 30列, 1010点を指定すれば、60600点にアクセスすることになり、元の100万未満のクエリよりも大幅に少なくなっていることが分かる。
更なる効率化1
フェルマーの小定理より、有限体$F_p$において$p-1$が$k$の倍数ならば、関数$x \to x^k$は$(p-1)/k+1$通りの値のみ出力することが知られている。
この数学的事実を基に更なる効率化を行う。まず、有限体の位数として10億より大きく、素数であり、$p-1$が$1000$の倍数である$p=1,000,005,001$を選ぶ。このとき、関数$x \to x^{1000}$は$1,000,006$個の出力しか持たない。
これを利用すると、正方形の列方向の値の個数は、$10$億から$1,000,006$に減少する。つまり、計算の複雑さは$10^{18}$から$10^{15}$に減少する。
この図を見ると、列方向が有限体で記述されているために、対角線がループしていることに気づく。つまり、一つの行に対角線上の点が1000点含まれているということである。この事実を利用すると、証明者は対角線上の値のみコミットすれば良く、検証者はある一組の行と列を指定すれば十分に証明を満足する結果が得られる。
ここら辺の理解が非常に難しいと思います。メンターの方によれば、「元の多項式$f(x)$を$(1 \leq x \leq 10^9)$の範囲で評価した結果(対角線)をコミットしておけば、任意の$y$(行)での値を1000個の$x$(列)で評価した結果と見做すことができる」ということみたいです。
更なる効率化2
先ほどの考え方を導入すると、証明プロセスは以下の様になる。
- 証明者は対角線の値のみ計算してコミットする
- 検証者は一組の列と行を指定する
- 証明者は列の値と、行の対角線上の1000点を提出する
- 検証者は列の値から次数1000未満の多項式を構成できること、対角線上の1000点から次数999の多項式を構成できること、列と行の交点が多項式上にあることを検証する
- 検証が通れば、証明者は提供した点の集合がある次数未満の多項式上にあることを証明できる
よって、計算の複雑さは$10^{15}$から$10^{9}$に減少する。
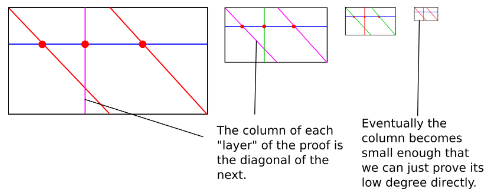
更なる効率化3
$f(x) = g(x, x^{1000})$ではなく、$f(x) = g(x, x^{2})$を採用すると、行方向は次数2の多項式、列方向は次数$D/2$の多項式となる。
列方向の多項式に同様の操作を再帰的に繰り返すと、計算の複雑さは以下の様になり、更なる効率化を達成できる。
D + \frac{D}{2} + \frac{D}{4} + \cdots = 2D