只今勉強中！機械学習 スカラー回帰の例：住宅価格の予想

スカラー回帰

前回は [只今勉強中！機械学習　多クラス分類の例：ニュース配信の分類] (https://qiita.com/minarai/items/58ffbe3c63773de70e59) の演習をしました。多クラス単一ラベル分類では複数のラベルのうちの１つを予測する問題でした。
回帰問題はラベルを予想するのではなく連続値を予測します。たとえば過去の株価から明日の株価を予測したり、過去の気温から明日の気温を予測したりします。
※回帰とロジスティック回帰は異なることに注意。ロジスティック回帰は分類アルゴリズムに属する。

住宅価格の予想

今回は1970年代中ごろのボストン近郊の住宅価格の中央値を予測する問題の演習をします。
予測データには部屋数や大きさ、犯罪発生率や税率などのデータ点が含まれています。
また、今回使用するデータ点は506個（404の訓練データと102個のテストデータ）しかなく、分類問題の時と比較して非常に少ないのが特徴的です。
入力データの特徴量はそれぞれ異なる尺度を使用（犯罪発生率、税率、部屋数など）している点も前回までの分類問題とは大きく異なる。

サンプルデータを読み込む

tutorial.py

# データ読み込み
from keras.datasets import boston_housing

(train_data, train_targets), (test_data, test_targets) = boston_housing.load_data()
# データの確認
print(train_data.shape)
>>> (404, 13)
print(test_data.shape)
>>> (102, 13)
print(train_data[0])
>>> [  1.23247   0.        8.14      0.        0.538     6.142    91.7
   3.9769    4.      307.       21.      396.9      18.72   ]

データの準備

特徴量のデータは価格や部屋の大きさ、部屋のタイプなど、値がバラバラなので正規化する必要がある
※正規化：価格も部屋の大きさも部屋のタイプも同じ基準の数値に揃えてあげる処理のこと
一般的に正規化で用いられる方法が「入力データを特徴量ごとに特徴量の平均値を引き、標準偏差で割る」である。

tutorial.py

# データを特徴量ごとに正規化する関数
def make_train_data(dataset, axis = 0):
    """
     特徴量ごとにデータを正規化する
     [手順]
     入力データを特徴量ごとに特徴量の平均値を引き、標準偏差で割る
     --------
     dataset:正規化するデータ
     axis   :軸を指定（データが2次元配列なら0 #列が対象)
    """
    mean = dataset.mean(axis) # 1軸目の平均値（2次配列なので各列の平均値）
    dataset -= mean # 平均値で引く
    std = dataset.std(axis) # 標準偏差
    dataset /= std # 標準偏差で割る
    
    return dataset

# 訓練でータを正規化
train_data = make_train_data(train_data, 0)
# テストデータも正規化
test_data = make_train_data(test_data, 0)

ニューラルネットワークの構築とモデルの定義

モデルを設計します。
レイヤー層のタイプ、出入力数、活性化関数のタイプ、そして層の数を設計します。
今回はモデルインスタンスを複数呼び出すk分割交差検証と呼ばれる方法を用いる為、model生成用の関数として定義し実装時に関数を呼び出すようにします。

tutorial.py

# モデルの定義
from keras import models
from keras import layers

"""
MEA
平均絶対誤差(mean absolute error)：予測値と目的地の誤差の絶対値の平均
"""
def build_model(train_data):
    # モデルインスタンスを生成するメソッド
    model = models.Sequential()
    model.add(layers.Dense(64, activation='relu', input_shape=(train_data.shape[1],)))
    model.add(layers.Dense(64, activation='relu'))
    model.add(layers.Dense(1))
    model.compile(optimizer='rmsprop', loss='mse', metrics=['mae'])
    return model

モデルの実装

k分割交差検証

• k分割交差検証とはデータセットをk個のサンプルセット（フォールド）に分割して、同じモデルのインスタンスもk個作成する。
  k個のモデルをk-1個のサンプルセットでの訓練と1回の検証を行い、最後に検証スコアの平均を求める方法。
  k値は4または5で行われることが多い。

tutorial.py

import numpy as np

# k分割交差検証データの生成
"""
エポック数を500に増やし、エポックごとに検証ログを保存するようにして再訓練と検証を行う
"""
num_epochs = 500
k          = 4
num_val_samples = len(train_data) // 4 # 小数点以下切り捨て
all_mae_histories = []
for i in range(k):
    print('processing fold #', i)
    # 検証データの準備：フォールドiのデータ
    key   = i * num_val_samples
    value = (i + 1) * num_val_samples

    val_data    = train_data[key:value]
    val_targets = train_targets[key:value]
    
    # 訓練データの準備：残りのフォールドのデータ
    partial_train_data = np.concatenate(
       [
          train_data[:key],
          train_data[value:]
       ],
       axis = 0
    )
    partial_train_targets = np.concatenate(
       [
          train_targets[:key],
          train_targets[value:]
       ],
       axis = 0
    )

    # モデルインスタンスを取得
    model = build_model(train_data)

    # モデルをサイレントモードで訓練と検証を実施
    history = model.fit(
            partial_train_data,
            partial_train_targets,
            validation_data = (val_data, val_targets),
            epochs = num_epochs,
            batch_size = 1,
            verbose = 0
    )
    # i回目の平均絶対誤差を取得して格納
    mea_history = history.history['val_mean_absolute_error']
    all_mae_histories.append(mea_history)

# k分割交差検証の平均スコアの履歴を作成
average_mae_history = [np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]

i回目の（訓練、検証）出力ログ

processing fold # 0
processing fold # 1
processing fold # 2
processing fold # 3

訓練（検証）データをプロット

tutorial.py

# 結果をプロット
import matplotlib.pyplot as plt

# このままだとグラフがみずらいので見やすくなるように修正
def smooth_curve(points, factor = 0.9):
    smoothed_points = []
    for point in points:
        if smoothed_points:
            previous = smoothed_points[-1]
            smoothed_points.append(previous * factor + point * (1 - factor))
        else:
            smoothed_points.append(point)
    return smoothed_points

smoothed_mea_history = smooth_curve(average_mae_history[10:])

plt.plot(range(1, len(smoothed_mea_history) + 1), smoothed_mea_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MEA')
plt.show()

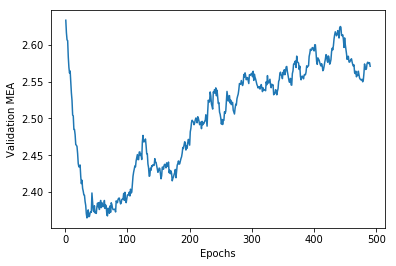
データの検証

上記プロットから検証スコア（MEA=平均絶対誤差）が30エポック付近で大きく改善され、その後過学習に陥っていることが伺える。
ということでモデルをチューニングしてもう一度訓練を実施する。

tutorial.py

import numpy as np


model = build_model(train_data)

# モデルをサイレントモードでfit
model.fit(
        train_data,
        train_targets,
        epochs = 30,
        batch_size = 8,
        verbose = 0 # サイレントモード
)

# 検証スコアを取得
test_mse_score, test_mea_score = model.evaluate(test_data, test_targets)


# 訓練結果出力
print(test_mea_score)
>>> 2.7296556491477815

振り返り

改めて30エポックでバッチサイズを8にして実行してみたが誤差は2700ほどと芳しくなかった。
この後、エポック数を調整していろいろ変えてみるも思わしい結果はでない。
本演習の目的は回帰問題のモデルの実装方法、そしてモデルのチューニング方法である。
モデルをチューニングするにあたって検証スコア（MEA=平均絶対誤差）をプロットし最小点を見つけ出すということがわかったので良しとする（肝心のテスト結果は芳しくないのだが、演習の教科書でも結果は思わしくないようである）。

まとめ

• 回帰ではデータを**正規化（一般的に正規化で用いられる方法が「入力データを特徴量ごとに特徴量の平均値を引き、標準偏差で割る」）**する。
• 損失関数は、**MSE（平均二乗誤差）**を用いることが多い。
• 評価関数は、**MEA（平均絶対誤差）**を用いることが多い。
• 利用可能なデータが少ない場合はk分割交差検証を用いることが有効。
• 利用可能な訓練データが少ない場合は隠れ層の数を少ない（1か2）小さなネットワークを使用する。