動画の足し算、引き算を用いて検索

はじめに

はじめまして、新入社員の三村です。
今年ももう終わりですね。
ドコモの会社の有志でAdventCalendarを書くことになったので、
普段は記事を読むだけの僕ですが、今回初めて記事を書きたいと思います。

概要

皆さんはどのように動画の検索を行いますか？
動画サイトで動画を検索するときは、何かキーワードを入れることが普通ですよね。
キーワード検索した動画の表示順序は、動画の再生数や過去の視聴履歴によりパーソナライズされて算出されます。
自分にとって気になる動画が表示されて便利ではあるのですが、時にはパーソナライズされすぎてしまい、
このところ私は上位に現れる同じような動画しか見なくなってしまいました。。。
そこで、面白い動画を見つけるため、今回は動画を雰囲気で検索する機械学習のモデルを作ってみました。
ここでは動画をベクトル化することで、動画同士をかけあわせるベクトル演算をできるようにしました。
以下のような計算が可能となります。

これにより、複数の動画の組み合わせで、検索したい動画の雰囲気を指定することが出来る様になります。
今回提案する技術の元となったのは、word2vec¹という手法です。
word2vecでは king - man + woman = queen のようなベクトル計算ができます。

今回は、このword2vecを応用して気分に合わせて**女性アイドルの動画-男性アイドルの動画+ヒップホップの動画**みたいなことをして動画を検索したいというのが今回のモチベーションです。

これを行うためにword2vecの拡張であるdocument2vec²を用いて動画をベクトル化します。これは動画という時系列データを対象としてベクトル化するためそれに適した手法として選びました。

本記事では、この結果を動画検索に利用した結果を提示します。

機械学習のモデル

今回のアイデアはすごく簡単で以下の3つの段階に分けることができます。

• 動画をあるまとまりを持った時間に分割・ラベル付けをします。
• 分割した動画をdocument2vecを用いてベクトル化します。
• ベクトル化した動画同士の足し算、引き算で別の動画を検索します。

まずは動画をセグメントに分割について。動画をセグメントに分けるのに人手でやっていては大変すぎて日が暮れてしまいます。そこで教師なし学習を用いて動画を分割していきましょう！

動画には音情報と画像情報があります。今回はこの２つの情報に基づいて動画を分割します！
私はもともとベイジアンだったので、ベイズ生成モデルを用いた分割を行いました。

• そもそもベイズとは？
  • 以下のような式で、事前確率、事後確率、尤度の関係を表現するもので、機械学習ではいろいろなところで使われています。
    

以下のようなベイズ生成モデルを構築しました！

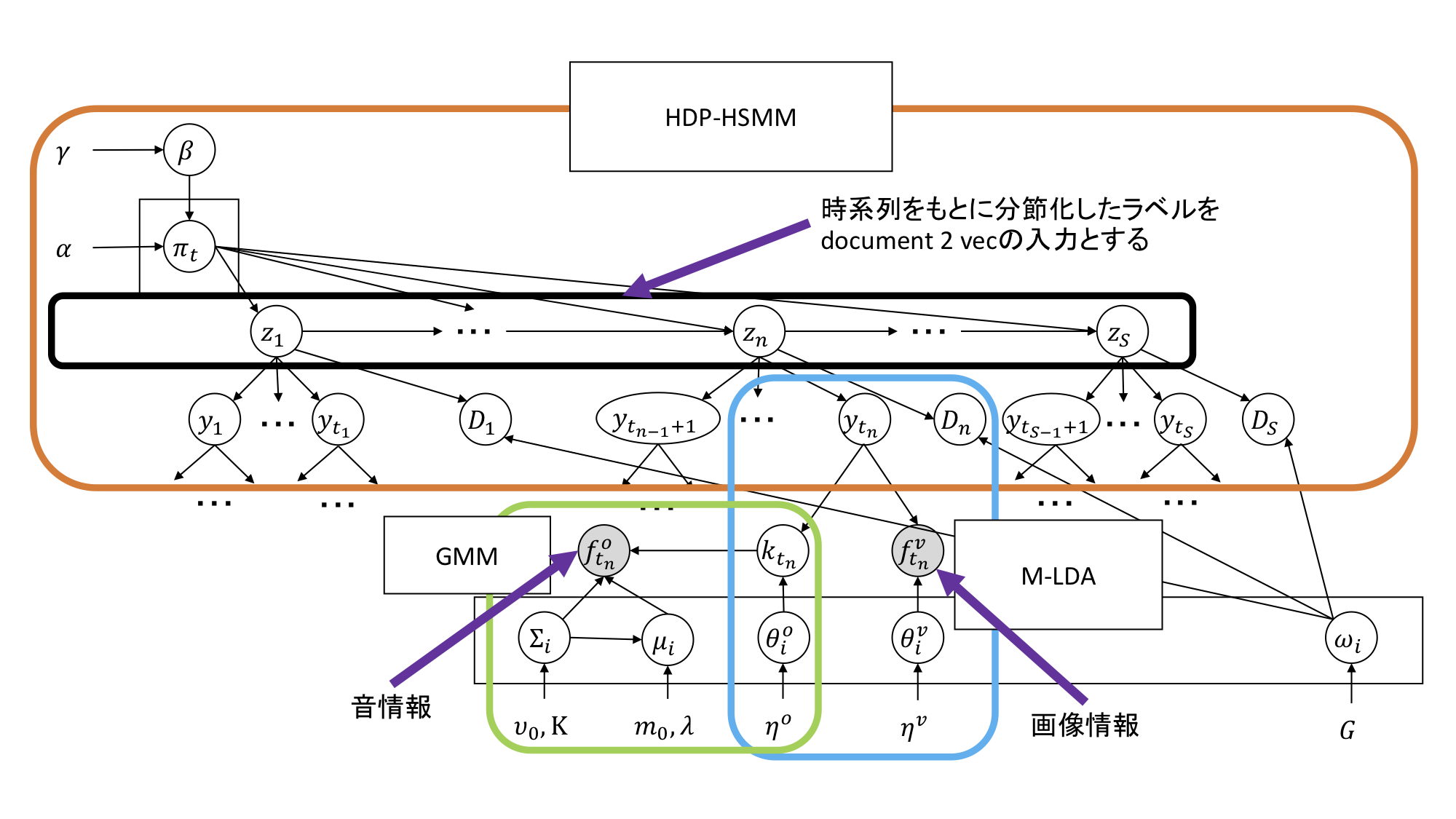
グラフィカルモデル

このモデルは基本的にはHDP-HSMM (Hierarchical Dirichlet Process Hidden Semi-Markov Model)³の拡張になっており、これにM-LDA (Multimodal latent Dirichlet allocation)⁴とGMM (Gaussian Mixture Model)⁵を組み合わせることで画像情報と音情報を組み合わせて動画を分割することができます。
今回は動画分割で与えられるクラスタ番号を文章の単語と捉え、これを用いて動画をベクトル化しました！

生成モデル

　今回作ったモデルはデータはある確率分布から生成されているという仮定をおいてそれに基づいて動画という時系列データを分割します。

以下にどのように生成したと仮定したのかを示します。

$$\beta \sim GEM(\beta|\gamma) $$

$$\pi_t \sim DP(\pi|\alpha,\beta) $$

$$z_t \sim g(z|\pi)$$

$$y_{t_s} \sim p(y|z)$$

$$D_n \sim p(D|z,\omega)$$

$$t_s = \sum_{s<{s^`}} D_{s_n}$$

$$\omega \sim p(\omega|G)$$

$$f_{t_n}^v \sim Multi(f^v|\theta_{y_{t_n}}^v)$$

$$f_{t_n}^o \sim \cal{N}(f^o|\mu_{k_{t_n}},\Sigma_{k_{t_n}})$$

$$k_{t_n} \sim Multi(k|\theta_{y_{t_n}}^o)$$

$$\mu_i \sim \cal{N}(\mu|m_0,(\lambda\Sigma_i^{-1})^{-1})$$

$$\Sigma_i^{-1} \sim \cal{W}(\Sigma^{-1}|v_0,K)$$

$$\theta^v \sim Dir(\theta^v|\eta^v)$$

$$\theta^o \sim Dir(\theta^o|\eta^o)$$

ここまでくれば準備は完成で分節化した動画をdocument2vecに入れてしまい、出てきた動画ベクトルを足し算引き算し、計算結果に最もコサイン類似度が高い動画を推薦するシステムを作ります。

実装

今回の実験では、ロイヤリティフリーの動画(948個)を用いてモデルを作成しました。
またdocument2vecはgensim⁶の実装を用います。
今回はGPUが入っていないマシンで機械学習のモデルを生成するため、できるだけ計算負荷を抑える必要があります。
そこで、画像特徴量はCNN⁷ではなくsift (Scale Invariant Feature Transform)⁸のopencv⁹の実装を用いて特徴量化しました。
音情報も同様に、計算負荷を考慮し、深層学習ではなく、mfcc (Mel-Frequency Cepstrum Coefficients)¹⁰を用いました。
ここまでは、すべてライブラリが揃っているので簡単に実装できます！
次にHDP-HSMMはpip install pyhsmm でインストールしてしまえばOKです。
最後にM-LDAだけは

class M_LDA():
	def __init__(self,data1,data2,num_class):
		self.num_iter  = 100
		self.num_class = num_class
		self.alpha     = np.ones([num_class])*10
		self.eta1      = np.ones([data1.shape[1]])*10
		self.eta2      = np.ones([data2.shape[1]])*10
		self.data1     = data1
		self.data2     = data2
		self.theta     = ss.dirichlet.rvs(self.alpha)
		self.beta1     = ss.dirichlet.rvs(self.eta1,num_class)
		self.beta2     = ss.dirichlet.rvs(self.eta2,num_class)
		self.z_i       = np.random.multinomial(1,self.theta[0],size=data1.shape[0])


	def fit(self):
		for gibbs in range(self.num_iter):
			print gibbs
			self.gibbs_sampling()


	def gibbs_sampling(self):
		self.beta1   =  self.dirichlet_multinomial1(self.eta1, self.data1,self.z_i)
		self.beta2   =  self.dirichlet_multinomial1(self.eta2, self.data2,self.z_i)
		self.theta   =  self.dirichlet_multinomial2(self.alpha,self.z_i)
		self.z_i     =  self.multinomial_multinomial()

	def dirichlet_multinomial1(self,eta,data,z_i):
		beta = np.ones([self.num_class,data.shape[1]])
		for i in range(self.num_class):
			beta[i]  = ss.dirichlet.rvs((z_i[:,i]*data.T).sum(1)+eta)
		return beta

	def dirichlet_multinomial2(self,alpha,z_i):
		return ss.dirichlet.rvs(alpha+z_i.sum(0))

	def multinomial_multinomial(self):
		self.log_beta1  = np.log(self.beta1)
		self.log_beta2  = np.log(self.beta2)
		self.z_i        = np.zeros([self.data1.shape[0],self.num_class])
		self.log_likely = self.data1.dot(self.log_beta1.T)+self.data2.dot(self.log_beta2.T)
		self.sub_theta  = self.theta * np.exp(self.log_likely-np.array([self.log_likely.max(1) for j in range(self.num_class)]).T)
		self.probab     = self.sub_theta/np.array([self.sub_theta.sum(1) for j in range(self.num_class)]).T
		for i in range(self.data1.shape[0]):
			self.z_i[i]    = np.random.multinomial(1,self.probab[i],size=1)
		return self.z_i
		
	def predict(self,new_data1,new_data2):
		self.new_data1 = new_data1
		self.new_data2 = new_data2
		log_beta1  = np.log(self.beta1)
		log_beta2  = np.log(self.beta2)
		z_i        = np.zeros([self.data1.shape[0],self.num_class])
		log_likely = self.new_data1.dot(log_beta1.T)+self.new_data2.dot(log_beta2.T)
		sub_theta  = self.theta * np.exp(log_likely-np.array([log_likely.max(1) for j in range(self.num_class)]).T)
		probab     = sub_theta/np.array([sub_theta.sum(1) for j in range(self.num_class)]).T
		for i in range(self.data1.shape[0]):
			z_i[i]    = np.random.multinomial(1,probab[i],size=1)
		return z_i

こんな感じで書いてしまってこれらを統合して学習できるようにsampling importance resamplingで推論できるように書き直せばOKです。

結果

これで動画をベクトル化して足し算したりできるようになりました。
このシステムを使うことで、これまでにない新しい動画に出会うことができるようになります！

https://www.youtube.com/watch?v=tWsPC2-nkAY
こんな動画と
https://www.youtube.com/watch?v=N5i9eZH4I9E
こんな動画を足し算すると
https://www.youtube.com/watch?v=1rTRyDbfti0
この動画が推薦されました。

https://www.youtube.com/watch?v=N5i9eZH4I9E
こんな動画から
https://www.youtube.com/watch?v=bNK62dXJS_g
こんな動画を引き算すると
https://www.youtube.com/watch?v=_EQHOcSaM28
こんな動画が推薦されます！

https://www.youtube.com/watch?v=bfeSNaybD0g
こんな動画と
https://www.youtube.com/watch?v=N58E5K0VYKU
こんな動画を足し算し
https://www.youtube.com/watch?v=30XOQJrpMP8
こんな動画を引き算すると
https://www.youtube.com/watch?v=PoHwMYq08K4
こんな動画が推薦されます！

結論から言えば精度がいいかと言われると疑問が残る結果にはなってしまいました。
しかし今回の目的は精度の良い検索技術を作ることではなく新しい動画に新しい方法で出会うことにあります。このため、この結果でもまぁいいかなと思います。。。（言い訳）

さいごに

これで気分に合わせて新しい動画を検索できる様になりました！
次はもっといいものを作るために深層学習の手法と組み合わせて行きたいと思います。
もっと詳しく中身が知りたいなどがありましたら、是非コメント・いいねをくださったら書かせていただきます！
今回のアドベントカレンダーの記事投稿はいい経験になりました。企画してくださった先輩方ありがとうございます！

参考文献

1. Goldberg, Yoav, and Omer Levy. "word2vec Explained: deriving Mikolov et al.'s negative-sampling word-embedding method." arXiv preprint arXiv:1402.3722 (2014). ↩

2. Le, Quoc, and Tomas Mikolov. "Distributed representations of sentences and documents." International Conference on Machine Learning. 2014.APA ↩

3. Johnson, Matthew J., and Alan Willsky. "The hierarchical Dirichlet process hidden semi-Markov model." arXiv preprint arXiv:1203.3485 (2012). ↩

4. MLANakamura, Tomoaki, Takayuki Nagai, and Naoto Iwahashi. "Bag of multimodal LDA models for concept formation." Robotics and Automation (ICRA), 2011 IEEE International Conference on. IEEE, 2011. ↩

5. Svensén, Markus, and Christopher M. Bishop. "Pattern Recognition and Machine Learning." (2007). ↩

6. http://cs231n.stanford.edu/index.html ↩

7. https://radimrehurek.com/gensim/ ↩

8. https://docs.opencv.org/3.4.3/da/df5/tutorial_py_sift_intro.html ↩

9. https://opencv.org/ ↩

10. http://speechresearch.fiw-web.net/66.html ↩