これは琉球大学アドベンドカレンダー16日目の記事です.
琉球大学OBのN/A3と書いて,なーさんと呼びます.投稿ギリギリでもうしわけないです.
1. はじめに
2014年にGoodfellow氏がGANを開発して以来,コンピュータが自動で画像を生成してくれる世界が到来しました.そして,年を重ねる毎に論文数も爆発的に増えて,深層学習 $\times$ 画像生成は広く認知された分野かと思います.
興味がある方は,以下のサイトたちがオススメです.前者はホットな論文を教えてくれるので,「こんなことができるのか!!」と驚きますし,後者はGANの歴史的論文を追っていくので,次何読めばいいか道を教えてもらえます.
そんな画像生成なのですが,実は正規性を担保したデータセットに対しては,(深層学習を使わなくても)単純な確率モデルでも生成や画像変形ができます.今日の内容は,じゃあどうやってやるんだって話をしていこうかと思います.
2. 平均画像と分散画像
単純に,画像を生成したい場合は,データ集めてきて,データの平均と分散を求めるだけでも画像生成はできます.(ただし,求めている画像かどうかは別)
ということで,レシピ. まずは,データを読み込む関数を作って,画像をロードしましょう.書くの忘れたけど,データセットMNISTでやってます.
from tensorflow.keras.datasets import mnist
import numpy as np
import pandas as pd
def load_data():
(x, y), _ = mnist.load_data()
mnist_df = pd.DataFrame(x.reshape(-1, 784) / 255.,
columns=['dim' + str(num+1) for num in range(784)])
mnist_df['target'] = y.reshape(-1, 1)
return mnist_df
mnist_df = load_data()
上記の関数から,データロードしたら,下図のような,データテーブルができます.
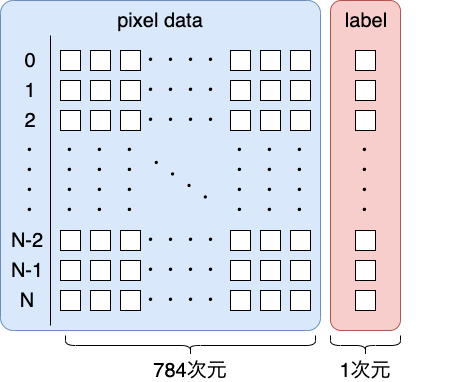
なぜラベルを引っ付けたのかというと,mnistの画像の輝度値からそのまま平均と分散を求めても, 下の画像のように雪玉画像しか生成されないためです.ですので,ラベル毎にデータを抽出して画像の生成を行おうかと思います.
ちなみに,画像かどうかを確認したい場合は,下記のおまじないを打てば確認できます.
(処理の流れ: 1.画像データのインデックス選択, 2.targetのカラムを除去, 3.numpy変換, 4.一次元データを28x28の二次元データ化)
import matplotlib.pyplot as plt
plt.imshow(mnist_df.iloc[0].drop(['target']).values.reshape(28, 28))
そして,おまじないの結果がコレ
2.1 ラベル毎に平均画像,分散画像の作成
表題の通り,ラベル毎に抽出して,平均画像と分散画像を生成してみましょう.
def img_write(name, data, norm=True):
data *= 255 if norm else data
data = np.array(data).astype(np.uint8)
cv2.imwrite(name, data.reshape(28,28))
def mnist_static_by_target_cat(df, column='target', norm=True):
for i, cat in enumerate(df[column].unique()):
cat_df = df.groupby(column).get_group(cat)
cat_df = cat_df.drop([column], axis=1)
img_write('mean_' + str(i) + '.jpg', cat_df.mean(), norm)
img_write('std_' + str(i) + '.jpg', cat_df.std(), norm)
mnist_static_by_target_cat(mnist_df)
そして,生成された画像が以下の通り.
なんかそれっぽい数字がなっているでしょう?
3. 画像変形(工事中)
時間がないので,サマリだけ・・・今週中には理論含めて綺麗に書きます.(すいません)
- 平均と分散を求めたので,正規分布を利用し,輝度値の変化を確率化
- しかし,これだけでは太さをいじれるだけなので,画像の変形方法も考えてみる.
- 輝度値ヒストグラムを確認すると,輝度値のピークが2つあるピクセルがあることに気がつく
- そこで,潜在変数2で混合ガウス分布関数を適用し,ピークが二つの分布に近似させた
- 結果として,より綺麗な画像が生成できるようになった.また,潜在変数の値を変化させると,画像を回転させられる.
以下,出力画像
-
平均と分散より求めた正規分布の確率を利用した画像
(左から, $P(輝度値)=[0.9, 0.99]$ 確率を0.9ずつ変化させた場合の画像の変化)

-
GMMを用いた潜在変数ごとの平均画像の変化
(また,混合ガウス分布は潜在変数ごとに正規分布を用意する.そのため、上記と同様にこちらのモデルでも,輝度確率を変化させれば,形状の太さの変更が可能.)
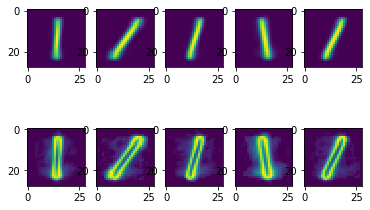
4.終わりに
今回,ノリと勢いだけで参加したのですが,文章ってやっぱり書くの難しいですね.締め切りがあればきっと書ききれると思ったのですが,現実は厳かったのです.後輩の皆様は,僕みたいなダメ人間を反面教師にして,スケジュール組んで活動に取り組めるようになっていただければと思ったり・・・
とにかく,次の記事は噂のjogo氏らしいので,僕なんかよりも為になるかと思います.それでは!!