実装で学ぶ深層学習~異常検知編(教師なし学習)~

#はじめに
この記事はAuto Encoderを実装、チューニング、考察する記事である。
#Target となる読者
1.異常検知を教師なしでするモデルを作りたい人
2.基礎的なニューラルネットワークを自身で読んで改良できる。

上記に当てはまる人に対しておすすめのモデルを提案する。

#異常検知の流れの説明
##問題設定
まず教師なしの異常検知とはなにかについて例を用いて説明する。
製品をつくるとどうしても不良品というものができてしまう。
その不良品の画像をとるとシワが目視できるような場合それを人が分離するのは非常に大変なのでニューラルネットワークで自動で検知してしまおうというものである。
しかしシワのついた画像が異常か正常かを2値分類するには足りない時に正常な画像のみを訓練に使って画像の異常値をもとめることができないかというものである。

##ベーシックなアプローチ
正常画像を入力として正常画像を返す関数:$f(x)=x$となる$f$をニューラルネットワークで学ぶ($x$は正常画像)。
異常値を$|x-f(x)|$によって定義すると$x$が正常画像なら0になるように訓練されているので小さくなるが、$x$が異常画像の場合ニューラルネットワークにとって初見のものなので$|x-f(x)|$は大きくなり,成立するというものだ。
このようなモデルをAuto Encoderと呼び,モデルの内部構造としては畳み込み層で小さくしてUp Sampling で画像を大きくして返すようなものが多い。（砂時計型）
ここでU-netなどの賢いモデルを使うと異常画像などに対しても予測がうまくいってしまいやすいので異常値をうまく取れないことに注意する。
##デノイズを行うアプローチ
上に書いたモデルだとある程度アホなモデルにして正常だとうまく予想するけど異常だと失敗するようなモデルを作る必要がある。
そこでモデルは最大限賢くして入力にノイズを加えたものを元に戻す(デノイズ),つまり$x=f(x+z)$($z$はノイズ)を学習するというものがそれなりによく動くようである。

##筆者のおすすめ
画像の予測を難しくする上でデノイズではなく超解像を用いるとうまく動くのではないかと当たりをつけて行ったところシワや傷を検知する問題においてかなり良いパフォーマンスになった。
ここまでに紹介した3つのアプローチを比較してどの程度差が出るかを示す。

#具体的実装
##問題設定
実際の製品の画像を使って結果を考察するのは権利の関係から行うことができないので問題がかなり簡単になってしまうが,mnistの手書き数字のうち1を正常画像、1以外の数字を異常画像として上記3つのアプローチを比較する。
##データの整理
コードの部分を全てコピーすれば動く形で紹介する。
kerasで実装を行う。
まずもろもろimportしてデータダウンロードする。

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from tensorflow.keras.datasets import mnist
from keras import layers
from keras import models
from keras import optimizers
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

データを扱いやすい形式に変換する

train_true = train_images[train_labels==1].reshape(6742,28,28,1)/255#訓練画像(1)は6742枚
test_true = test_images[test_labels==1].reshape(1135,28,28,1)/255#検証の正常画像(1)は1135枚
test_false = test_images[test_labels!=1].reshape(8865,28,28,1)/255#検証の異常画像(1以外)は1032枚

mnistのデータセットは0~9まで枚数が均一だと思っていたがバラバラのようだ。
画像は[0,1]の範囲に正規化した。

##モデルの定義

model1をただのエンコーダデコーダmodel1を定義

ffc = 8#first filter count
model1 = models.Sequential()
model1.add(layers.Conv2D(ffc,(3,3),padding="same",activation="relu",input_shape = (28,28,1)))
model1.add(layers.BatchNormalization())
model1.add(layers.MaxPooling2D((2,2)))
model1.add(layers.Conv2D(ffc,(3,3),padding="same",activation="relu"))
model1.add(layers.BatchNormalization())
model1.add(layers.MaxPooling2D((2,2)))
model1.add(layers.Conv2D(ffc,(3,3),padding="same",activation="relu"))
model1.add(layers.BatchNormalization())
model1.add(layers.UpSampling2D())
model1.add(layers.Conv2D(ffc,(3,3),padding="same",activation="relu"))
model1.add(layers.BatchNormalization())
model1.add(layers.UpSampling2D())
model1.add(layers.Conv2D(ffc,(3,3),padding="same",activation="relu"))
model1.add(layers.BatchNormalization())
model1.add(layers.Conv2D(1,(3,3),padding="same",activation="sigmoid"))
model1.compile(loss = "mae",optimizer="adam")
model1.summary()

ここで畳み込みと畳み込みの間にバッチ正則化をほどこした。
出力層の活性化はsigmoidである。([0,1]に写像するため)
損失関数はMAEで二乗誤差でなく絶対値を使った方が画像生成ではボケづらいなどの利点がある。
同様にmodel2を定義していった。

ffc = 8#first filter count
model2 = models.Sequential()
model2.add(layers.MaxPooling2D((4,4),input_shape = (28,28,1)))
model2.add(layers.UpSampling2D())
model2.add(layers.Conv2D(ffc,(3,3),padding="same",activation="relu"))
model2.add(layers.BatchNormalization())
model2.add(layers.Conv2D(ffc,(3,3),padding="same",activation="relu"))
model2.add(layers.BatchNormalization())
model2.add(layers.UpSampling2D())
model2.add(layers.Conv2D(ffc,(3,3),padding="same",activation="relu"))
model2.add(layers.BatchNormalization())
model2.add(layers.Conv2D(ffc,(3,3),padding="same",activation="relu"))
model2.add(layers.BatchNormalization())
model2.add(layers.Conv2D(1,(3,3),padding="same",activation="sigmoid"))
model2.compile(loss = "mae",optimizer="adam")
model2.summary()

maxpooling のみを行ってエンコードすることでデコードに計算材料をさいている。

##訓練と結果
それでは実際に訓練してみよう。

###通常のエンコーダデコーダ

t_acc = np.zeros(50)
f_acc = np.zeros(50)
for i in range(50):
  hist = model1.fit(train_true,train_true,steps_per_epoch=10,epochs = 1,verbose=0)
  true_d = ((test_true - model1.predict(test_true))**2).reshape(1135,28*28).mean(axis=-1)
  false_d = ((test_false- model1.predict(test_false))**2).reshape(8865,28*28).mean(axis=-1)
  t_acc[i] = (true_d<=true_d.mean()+3*true_d.std()).sum()/len(true_d)
  f_acc[i] = (false_d>true_d.mean()+3*true_d.std()).sum()/len(false_d)
  print("{}週目の学習正常画像の正答率は{:.2f}%で、異常画像の正答率は{:.2f}%です".format(i+1,t_acc[i]*100,f_acc[i]*100))
plt.plot(t_acc)
plt.plot(f_acc)
plt.show()

異常値の導出は損失関数と違い二乗誤差をもちいた。
これを行うとmodel1つまり普通のエンコーダデコーダが訓練する中で正常画像と異常画像をそれぞれどの程度正しく判断できたかの確率の推移を表したグラフが出力される。
閾値を正常画像の$\mu(平均)+3\sigma(標準偏差)$とおいた。

以下出力例

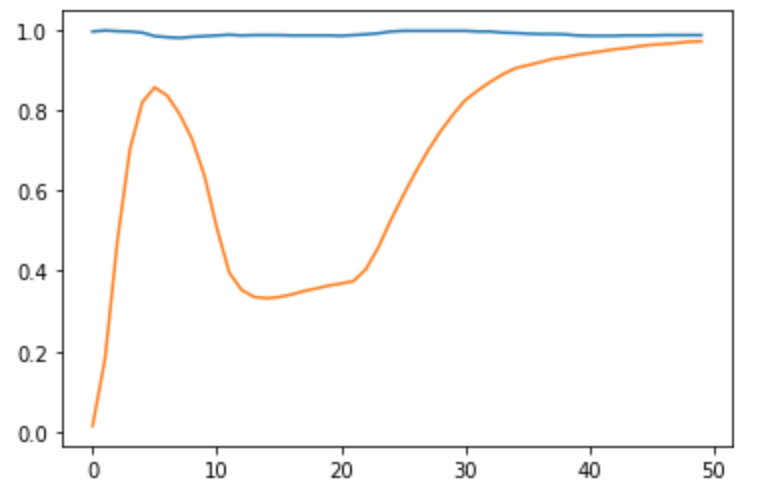
青は正常画像を正常と判断する確率の推移でオレンジが異常画像を異常画像と判断するの確率の推移である。
正常画像の平均から上に標準偏差3つ分のところに常に閾値があるので正常画像を正常画像と判断する確率は常に98%程度である。
50epoch程度で十分学習できたようだ。
(最終値は正常画像の正答率が98.68%で、異常画像の正答率は97.13)

###ノイズ付きエンコーダデコーダ
モデルはmodel1を用いて入力に0中心でscale0.1で学習するサイズと同じサイズのノイズを加えて学習を行う。具体的なコードは以下の通りである。

t_acc = np.zeros(50)
f_acc = np.zeros(50)
for i in range(50):
  hist = model1.fit(train_true,train_true+0.1*np.random.normal(size=train_true.shape),steps_per_epoch=10,epochs = 1,verbose=0)
  true_d = ((test_true - model1.predict(test_true))**2).reshape(1135,28*28).mean(axis=-1)
  false_d = ((test_false- model1.predict(test_false))**2).reshape(8865,28*28).mean(axis=-1)
  t_acc[i] = (true_d<=true_d.mean()+3*true_d.std()).sum()/len(true_d)
  f_acc[i] = (false_d>true_d.mean()+3*true_d.std()).sum()/len(false_d)
  print("{}週目の学習正常画像の正答率は{:.2f}%で、異常画像の正答率は{:.2f}%です".format(i+1,t_acc[i]*100,f_acc[i]*100))
plt.plot(t_acc)
plt.plot(f_acc)
plt.show()

これを実行すると以下のようなグラフが得られる。

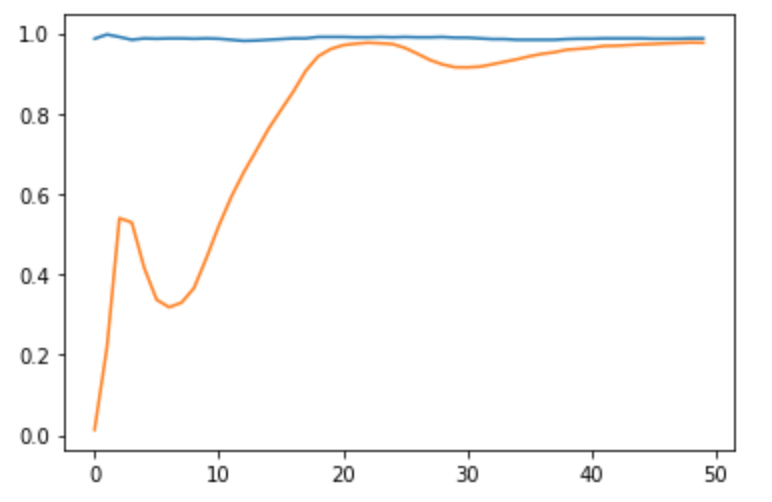
収束がある程度早くなったようだ。
最終値は正常画像の正答率が98.68%で、異常画像の正答率は97.59％であった。

###超解像的アプローチ
それではmodel2を訓練して結果を見てみよう。

t_acc = np.zeros(50)
f_acc = np.zeros(50)
for i in range(50):
  hist = model2.fit(train_true,train_true,steps_per_epoch=10,epochs = 1,verbose=0)
  true_d = ((test_true - model2.predict(test_true))**2).reshape(1135,28*28).mean(axis=-1)
  false_d = ((test_false- model2.predict(test_false))**2).reshape(8865,28*28).mean(axis=-1)
  t_acc[i] = (true_d<=true_d.mean()+3*true_d.std()).sum()/len(true_d)
  f_acc[i] = (false_d>true_d.mean()+3*true_d.std()).sum()/len(false_d)
  print("{}週目の学習正常画像の正答率は{:.2f}%で、異常画像の正答率は{:.2f}%です".format(i+1,t_acc[i]*100,f_acc[i]*100))
plt.plot(t_acc)
plt.plot(f_acc)
plt.show()

結果グラフ

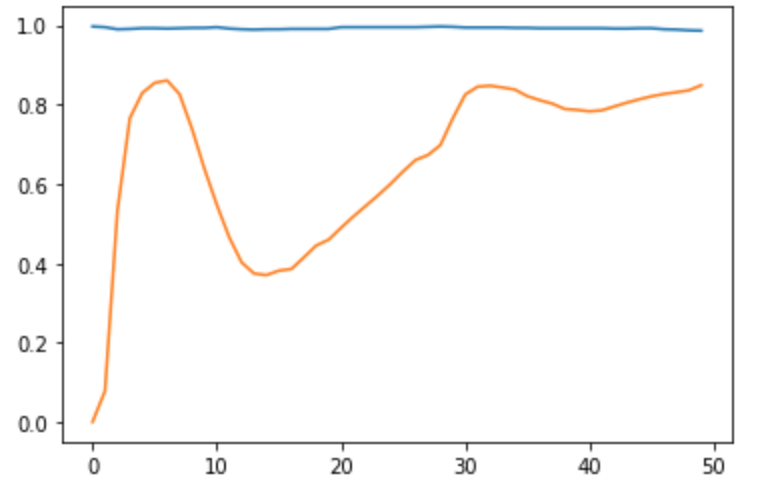
想像以上にだめなモデルであった。
最終値も収束していなさそうだが正常正答率が98.59%で、異常画像の正答率は84.85％であった。

#結論
手書き文字の1を見て1とそれ以外を区別していったがこの問題の場合ノイズを加えるのが効果的であることがわかった。それはこのノイズを加えるという操作で1は7に見えたり9に見えたりするのでそれを1に戻すのに慣れたモデルが精度向上をするのはかなり目に見えている。
つまり異常の種類がわかっていればその種類の異常を付け足すような変換をしてそれを戻すという訓練を入れるとAuto Encoder の性能は非常に高くなると考えられる。

今回のデータセットでおすすめした超解像的アプローチがあまり効果を得なかったが、実際の工業製品のシワや傷を検知する場合解像度を落としてシワや傷を一度見えなくしてから復元するというアプローチが効果的なケースもあるので、対象となる問題を見ながら使うモデルを変えていくといいだろう。