はじめに
Pythonで機械学習などを扱っていると,二次元以上の多次元の行列を可視化したくなりますよね.
自分用メモとしてスニペットを載せます.
前提
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
Qiita記事用に使用するデータはすべてランダムデータ
matrix_2d = np.random.rand(5, 5)
matrix_3d = np.random.rand(5, 5, 5)
2次元
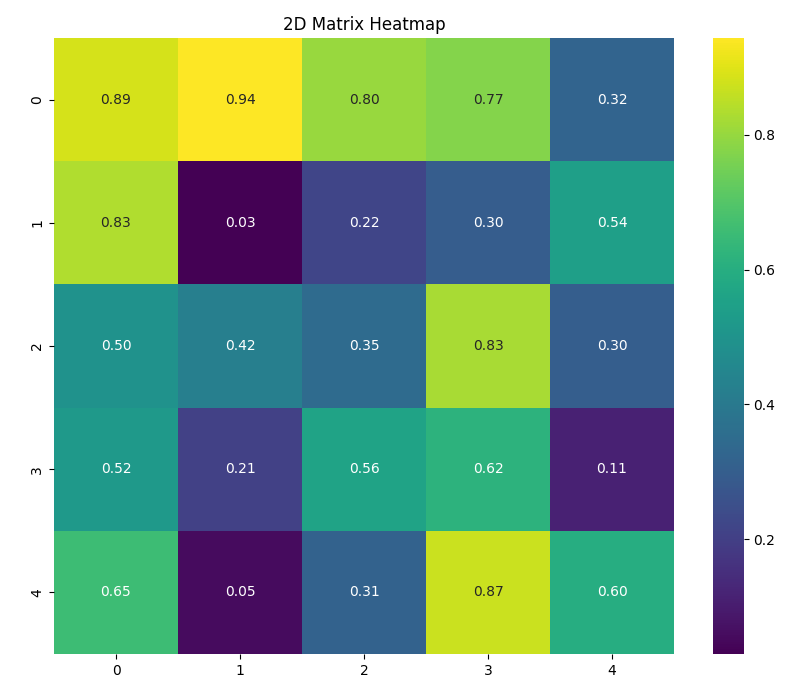
ヒートマップ
大体の可視化手法はこれに勝てない.
ヒートマップ亜種みたいなものがたくさんある.
plt.figure(figsize=(10, 10))
sns.heatmap(matrix_2d, annot=True, fmt=".2f", cmap='viridis')
plt.title('2D Matrix Heatmap')
plt.show()
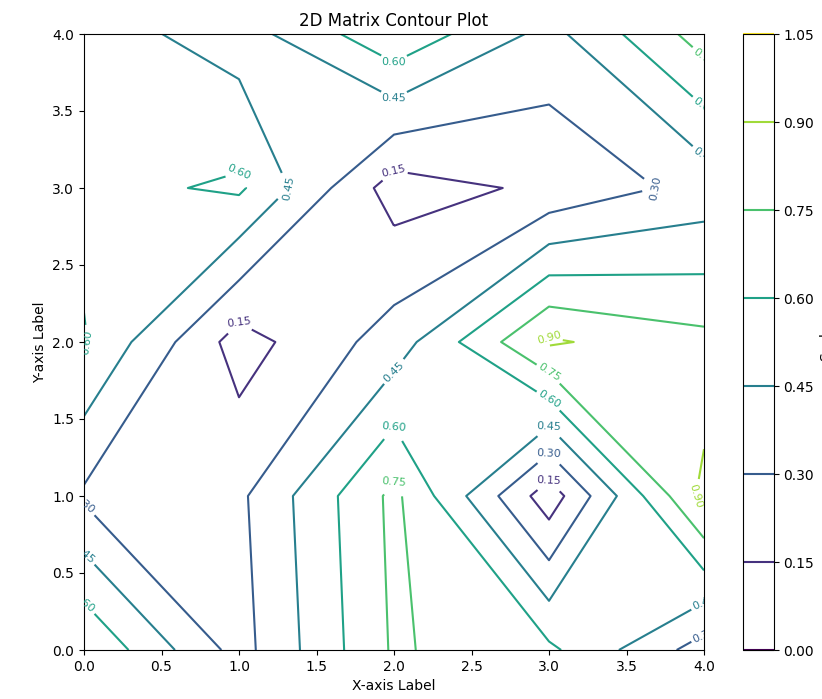
等高線
plt.figure(figsize=(10, 8))
contour = plt.contour(matrix_2d, cmap='viridis')
plt.clabel(contour, inline=True, fontsize=8)
plt.colorbar(contour, label='Scale')
plt.title('2D Matrix Contour Plot')
plt.xlabel('X-axis Label')
plt.ylabel('Y-axis Label')
plt.show()
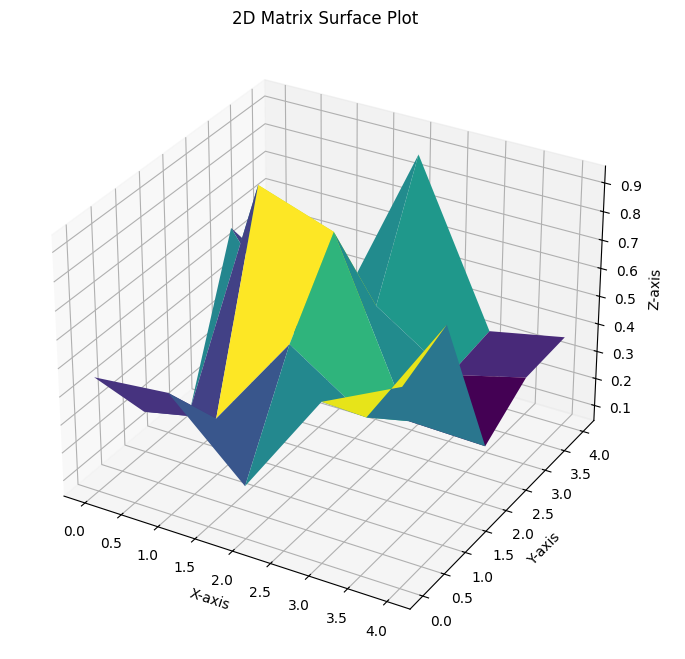
3Dプロット
from mpl_toolkits.mplot3d import Axes3D
x = np.arange(matrix_2d.shape[0])
y = np.arange(matrix_2d.shape[1])
x, y = np.meshgrid(x, y)
z = matrix_2d
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, cmap='viridis')
plt.title('2D Matrix Surface Plot')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
ax.set_zlabel('Z-axis')
plt.show()
3次元
ちゃんと傾向がはっきりしているデータなら可視化しやすいが,そうでないなら可視化より他の統計的な手法で分析した方がいい.
複数ヒートマップ
2次元ヒートマップをいくつも並べるだけ
for i in range(matrix_3d.shape[2]):
plt.figure(figsize=(6, 5))
sns.heatmap(matrix_3d[:, :, i], annot=False, cmap='viridis')
plt.title(f'Slice {i+1} of 3D Matrix')
plt.show()
Axes3D
数字の格納されている場所のプロット
0と1や0と小数など,0がいっぱい入っているようなSparseな行列の可視化には使えるかも?
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
x, y, z = matrix_3d.nonzero()
ax.scatter(x, y, z, c=matrix_3d[x, y, z], cmap='viridis')
plt.title('3D Matrix Scatter Plot')
plt.show()

マーチングキューブ法
点の配置に規則性があるなら,メッシュを張れば何か分かるかもしれない.
そんなデータはあまりなさそうな気もする.
from skimage import measure
verts, faces, _, _ = measure.marching_cubes(matrix_3d, level=0.5)
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
ax.plot_trisurf(verts[:, 0], verts[:, 1], faces, verts[:, 2], cmap='Spectral', lw=1)
plt.title('3D marching cubes Plot')
plt.show()

多次元
可視化というよりは,可視化したい次元をどう選択するか,どう処理して次元を削減するか,といったことを考えた方が良さそう
4次元データ: 複数のAxes3D
単純だが分かりにくい
for i in range(matrix_4d.shape[3]):
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
data_slice = matrix_4d[:, :, :, i]
x, y, z = data_slice.nonzero()
ax.scatter(x, y, z, c=data_slice[x, y, z], cmap='viridis')
plt.title(f'Slice {i+1} of 4D Matrix')
plt.show()
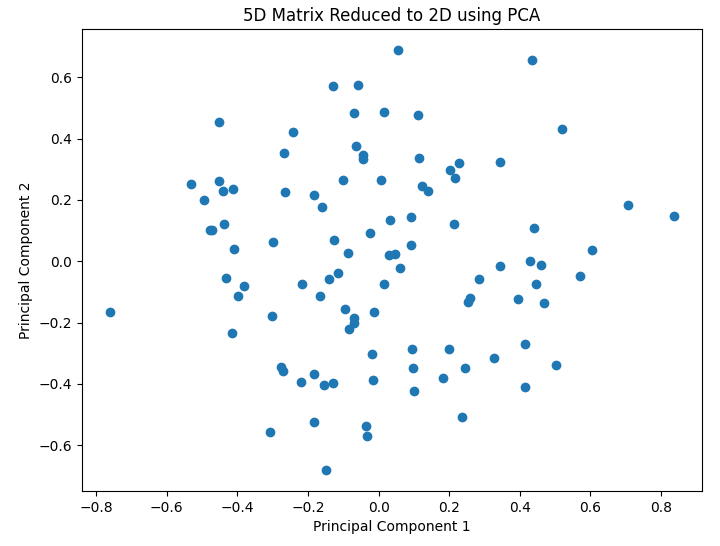
主成分分析
皆さんご存じ主成分分析.
ライブラリが勝手にやってくれるが,主成分分析が効くようなデータであることが前提
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
reduced_matrix = pca.fit_transform(matrix_5d)
plt.figure(figsize=(8, 6))
plt.scatter(reduced_matrix[:, 0], reduced_matrix[:, 1])
plt.title('5D Matrix Reduced to 2D using PCA')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.show()
t-SNE
こちらも主成分分析と同様に次元圧縮の手法.
特に可視化に使用することを意図しているらしい.
sklearnが勝手にやってくれるので,使用感はPCAと一緒.
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, random_state=42)
reduced_matrix_tsne = tsne.fit_transform(matrix_5d)
plt.scatter(reduced_matrix_tsne[:, 0], reduced_matrix_tsne[:, 1])
UMAP
非線形データでもいけるらしい.
import umap
reducer = umap.UMAP(n_components=2)
embedding = reducer.fit_transform(matrix_5d)
plt.scatter(embedding[:, 0], embedding[:, 1])
MDS
データの位置関係を大事にするらしい.
from sklearn.manifold import MDS
mds = MDS(n_components=2, random_state=42)
mds_result = mds.fit_transform(matrix_5d)
plt.scatter(mds_result[:, 0], mds_result[:, 1])
さいご
行列の可視化手法って,亜種みたいなものは多いですが,アイデア自体は思ったより少ないですね……筆者が見つけられていないだけかも