週streakが切れそうだけど書けそうなことが他に思いつかないから
E - Forbidden Prefix を自分が解いたやり方が解説タブに載っていなそうだったから、ここに記す。
問題概要
- 指定の文字列を多重集合 $X$ に追加する
- 指定の文字列を多重集合 $Y$ に追加する
の2種類のクエリが与えられる。
各クエリを実行した後、毎回「$Y$ の要素のうち、どの接頭辞も $X$ の要素でないもの」の個数を出力する。
自分の解き方概要
- それぞれの $Y$ に追加する文字列について、どのクエリでカウント対象外になる (すなわち、最初に接頭辞が $X$ に追加される) かを求める
- 「これまでに $Y$ に追加された文字列の個数」から「これまでに $Y$ に追加された文字列のうち、このクエリまでにカウント対象外になったものの個数」を引くことで、求めたい個数を求める
自分の解き方
提出 #66046051 - AtCoder Beginner Contest 403(Promotion of AtCoder Career Design DAY)
クエリ列の走査を2回行い、2回目で答えを出力する。
1パス目
$X$ に追加するそれぞれの文字列について、どのクエリで追加されるかを Trie に登録する。
複数回追加される文字列は、最も早いクエリを登録する。
ここでは、文字列を $Y$ に追加するクエリは処理しない。
Trie は、根付き木の一種で、根 (空文字列に対応する) から初めて文字列の各文字に対応する辺をたどっていくことで、文字列に対応する頂点に行くことができるデータ構造である。
今回は、$X$ に追加する文字列に対応する頂点に、その文字列が追加されるクエリの番号を書き込むことを、「登録する」という。
(その途中に通る) $X$ に追加する文字列に対応しない頂点には、$\infty$ を書き込んでおく。
たとえば
- $X$ に
fooを追加 - $X$ に
barを追加 - $Y$ に
bazを追加 - $X$ に
baを追加 - $X$ に
bazを追加 - $Y$ に
booを追加
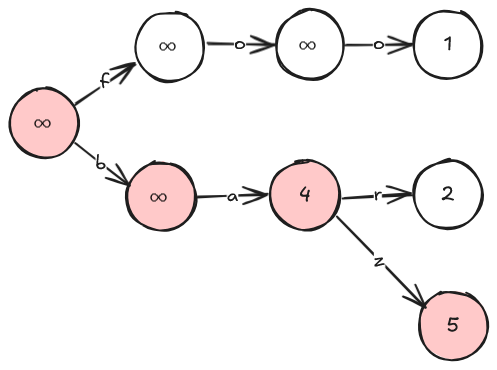
というクエリ列では、以下の Trie になる。
クエリ 3 およびクエリ 6 は $Y$ への追加なので、今回の処理の対象外である。
2パス目
BIT (Binary Indexed Tree) を用いて処理を行う。
BITは、
- 指定した要素への値の加算
- 最初の要素から指定した要素までの値の和
を効率よく行うことができるデータ構造である。
Y に追加するクエリで行う処理
1パス目で作成した Trie を用いて、追加する文字列の接頭辞が最初にどのクエリで $X$ に追加されるかを求める。
このとき、接頭辞も考慮するので、追加する文字列に対応する頂点だけでなく、その頂点に行く途中で通る頂点についても書き込まれた値をチェックし、それらの最小値を用いる。
たとえば、先ほど例示したクエリ列の 3 番目で追加する baz については、以下の赤く塗った頂点をチェックし、($\infty, \infty, 4, 5$ の最小値は 4 なので) 最初にクエリ 4 で $X$ に追加されることがわかる。
途中で行くべき頂点が無くなってしまった場合は、それ以降に $\infty$ が書き込まれた頂点があるとみなす。
たとえば、先ほど例示したクエリ列の 6 番目で追加する boo については、以下の赤く塗った頂点をチェックする。
頂点が無くなった時点で、それ以降の頂点はすべて $\infty$ とみなすので、探索を打ち切ってよい。
今回は、最初に $X$ に追加されるクエリは $\infty$ (すなわち、追加されない) である。
追加する文字列の接頭辞が最初に $X$ に追加されるクエリを求めたら、そのクエリの位置に対応する BIT の要素に 1 を加算する。
すなわち、たとえばクエリ 4 で追加される場合は、4 番目の要素に 1 を加算する。
追加されない場合は、最後のクエリに対応する要素よりも後の適当な要素に 1 を加算する。
全てのクエリで行う処理
$Y$ に追加するクエリの場合は、前述の処理を行った後でこれを行う。
BIT を用いて、以下を求める。
- これまでに $Y$ に追加された文字列の総数
- これまでに $Y$ に追加された文字列のうち、このクエリまたはそれより前のクエリで接頭辞が $X$ に追加された文字列の数
前者は、接頭辞が $X$ に追加されない場合に 1 を加算する要素までの和である。
後者は、このクエリに対応する要素までの和である。
これらを求めたら、前者から後者を引くことで、求めたい数が求まる。
たとえば、前述のクエリ列の 3 番目のクエリを処理すると、文字列の総数は 1、接尾辞が $X$ に追加された文字列の数は 0 なので、求めたい数は $1 - 0 = 1$ である。
4 番目のクエリでは、baz の接頭辞である ba が $X$ に追加される。
すると、文字列の総数は 1、接尾辞が $X$ に追加された文字列の数は 1、求めたい数は $1 - 1 = 0$ となる。
6 番目のクエリの処理では、文字列の総数は 2、接尾辞が $X$ に追加された文字列の数は 1、求めたい数は $2 - 1 = 1$ となる。
考え直した結果
提出 #66375663 - AtCoder Beginner Contest 403(Promotion of AtCoder Career Design DAY)
2 パス目を
- 現在の答えを、変数で持っておく
- $Y$ に文字列を追加するクエリでは
- この文字列の接頭辞が最初に $X$ に追加されるクエリを求める
- それが今のクエリかそれより前のクエリであれば、何もしない (捨てる)
- 後のクエリで追加される、もしくは追加されないならば、現在の答えに 1 を加算し、追加されるクエリでの答えの減算を予約する
- 予約されている答えの減算を実行し、現在の答えを出力する
とすることで、BIT を使わずに答えを求めることができる。
答えの減算の予約は、減算を行うクエリに対応する配列の要素に減算する値を加えることで行う。
減算の予約が行われていないクエリでは、0 を減算する予約が行われているとみなす。
計算量
クエリ数を $Q$、全てのクエリで与えられる文字列の文字数の和を $L$ とする。
時間計算量
それぞれのクエリで与えられる文字列内の各文字について、Trie のノードを高々 1 回ずつたどるので、1 パス目と 2 パス目の Trie の操作はあわせて $O(L)$ である。
2 パス目では、要素数がクエリ数程度の BIT の操作を各クエリで高々定数回行うので、$O(Q \log Q)$ である。
あわせて、この解き方の計算量は $O(L + Q \log Q)$ である。
BIT を使わないバージョンでは、2 パス目の操作のうち Trie の操作を除く部分はそれぞれのクエリについて高々定数時間でできるので、$O(Q)$ となり、計算量は $O(L + Q)$ である。
ここで、各クエリで与えられる文字列の長さは 1 以上なので、$Q \leq L$ である。
よって、この計算量は $O(L)$ と表せる。
空間計算量
クエリ列の保存に $O(Q + L)$ かかる。
それぞれのクエリで与えられる文字列内の各文字について、Trie のノードを高々 1 個作るので、Trie の構築に $O(L)$ かかる。
BIT または答えの減算の予約に要素数がクエリ数程度の配列を用い、これは $O(Q)$ である。
あわせて $O(L + Q)$ であるが、$Q \leq L$ なので、これは $O(L)$ と表せる。
おまけ
競技プログラミングなので安全性はあまり考慮しなくてよいが、気持ち悪いので配列の範囲外アクセスをなるべく防ぎたいとする。
このとき、26 要素の配列 hoge および整数 idx に対して
if ('a' <= idx && idx <= 'z') {
// hoge[idx - 'a'] を用いた処理
}
としてしまうと、'a' から 'z' までのコードが連続していない文字コードでは範囲外アクセスが行われてしまう恐れがある。
今回、配列は「26 要素」だとわかっているので、この数字をそのまま用いて
if ('a' <= idx && idx < 'a' + 26) {
// hoge[idx - 'a'] を用いた処理
}
としたほうが、安全性は高まるだろう。
ただし、このコードでも
- マジックナンバーの
26を条件式に使うのはよくない -
'a'から'z'までのコードが連続していない文字コードでは、範囲外アクセスにはならないものの、仕様の範囲内 (アルファベット小文字) でも処理に失敗する入力が出てくる
といった問題点がある。
まあ、どうせ杞憂なので、気にして対応したい奴だけ気にして対応すればよい。
今回の実装では、文字列の終端 (\0) の判定を、この「アルファベット小文字でない」という条件式で行っている。
まとめ
- それぞれの文字列が $X$ に追加されるクエリの位置を Trie で管理する
- これまでに $Y$ に追加された文字列のうち、まだ無効化 (接頭辞が $X$ に追加) されていないものの数を答える
ことで、時間計算量・空間計算量ともに $O(L)$ でこの問題を解くことができた。($L$ はクエリで与えられる文字列の長さの和)