「中心からの距離を計算し、それが半径以下だったら点を描く」という方法で円を描くとき、適当に実装してしまうと、このような偏った美しくない円になってしまうことがある。
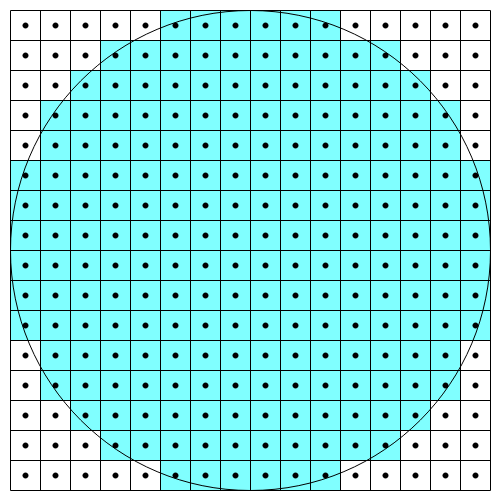
本記事では、このような円ではなく、以下のような対称的なきれいな円を描く方法を紹介する。
悪い実装
以下のような疑似コードで円を描くと、偏ってしまう。
# 縦 diameter、横 diameter の正方形の中に直径 diameter の円を描く
def draw_circle_bad(diameter):
# 円の中心の座標
cx = diameter / 2
cy = diameter / 2
# 円の半径
radius = diameter / 2
# 円を描画する
for y in range(diameter):
for x in range(diameter):
# 円の中心からの距離を計算・判定する
dx = x - cx
dy = y - cy
if dx * dx + dy * dy <= radius * radius:
# 円の中なので、点を描画する
draw_point(x, y)
これは、各ピクセルに点を描画するかの判定を各ピクセルの左上の点で行うことに相当するので、画像の左上のほうが右下のほうよりも中心から遠いという判定になりやすくなるためである。
良い実装
「悪い実装」では、各ピクセルの左上の点で判定を行ったのが描画が偏った原因である。
そのため、それぞれの座標に 0.5 を足し、各ピクセルの中央の点で判定を行うことで、描画の偏りを解消できる。
# 縦 diameter、横 diameter の正方形の中に直径 diameter の円を描く
def draw_circle_bad(diameter):
# 円の中心の座標
cx = diameter / 2
cy = diameter / 2
# 円の半径
radius = diameter / 2
# 円を描画する
for y in range(diameter):
for x in range(diameter):
# 円の中心からの距離を計算・判定する
# 0.5 を足し、ピクセルの中心で判定する
dx = x + 0.5 - cx
dy = y + 0.5 - cy
if dx * dx + dy * dy <= radius * radius:
# 円の中なので、点を描画する
draw_point(x, y)
結論
各点の中心からの距離に基づいて円を描画する際、点 (ピクセル) の中心の座標で距離の計算を行うと、対称性が向上したよりきれいな円を描画できることがある。
おまけ
今回の記事に掲載した画像を作成するために実装したプログラムを公開した。