1.はじめに
業務で時系列データ解析を担当している中で、たまたま本屋で参考資料[1]を見かけ、量子コンピューティングと時系列データ予測でリンクしている部分があると知り、個人で勉強を進めていた。
アドベントカレンダー(量子コンピュータ)も見かけ、せっかくなので勉強したことをまとめ、同じ分野に興味を持っている同志との出会いを期待し、本記事を作成する。
2.参考資料
[1] 今野紀雄著、量子ウォークによる時系列解析、日本評論社、2020年9月
[2] webマガジン「RAD-IT21」,ランダムウォークから量子ウォークへ
[3] a memory less ephemeral 実装例
[4] 今野紀雄著、量子ウォークの過去・現在・未来, 2013年5月
[5] Qiita記事,量子ウォークの量子コンピュータ実装1、2019年12月
3.量子ウォークと時系列解析
3-1. ランダムウォーク
・いわゆる酔歩。
・確率$p$で右に、確率$(1-p)$で左に動く、1次元のランダムウォークを考える。
・$ \Phi[x,t] $が、時刻tに、地点xにいる確率とする。
・$ \Phi[x,t+1] = p*\Phi[x-1,t] + (1-p)*\Phi[x+1,t] $ で表される場合を、ランダムウォークという。
・株価の時系列データなどは、ランダムウォークでうまく表現できることが知られている。
3-2. 量子ウォーク
・ランダムウォークの量子版。
・確率の表現に、量子コインを用いている。
・一番基礎的な手法に、「アダマールウォーク」がある。本ページでは、アダマールウォークの実装例を記載する。
4.実装例
4-1. ランダムウォーク
ランダムウォークの実装例を以下に示す。
import numpy as np
import random
from matplotlib import pyplot as plt
N_steps = 1000
prob = 0.5
def SimpleRandomWalk(N, p, line):
position = np.empty(N)
position[0] = 0
pos_counter = 0
steps = np.arange(N)
#ランダムウォークスタート
for i in range(1,N):
test = random.random()
if test >= p:
pos_counter += 1
else:
pos_counter -= 1
position[i] = pos_counter
plt.plot(steps, position, line)
plt.xlabel('Steps taken')
plt.ylabel('Distance from Starting Position')
return position
position_distribution = []
for i in range(1000):
p = SimpleRandomWalk(N_steps, prob, line="-")
position_distribution.append(p[-1])
plt.figure()
plt.hist(position_distribution)
plt.show()
ランダムウォークの軌跡を以下に示す。
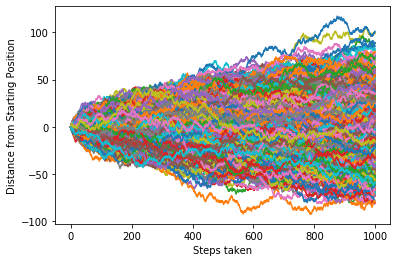
Fig.1 ランダムウォークの軌跡(Step=1000の場合)
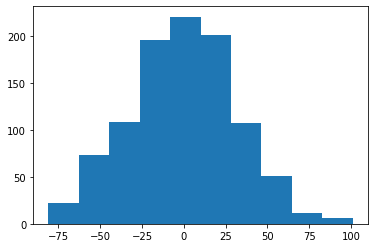
Fig.2 ランダムウォークのゴール地点の確率分布(Step=1000の場合)
4-2. 量子ウォーク
量子ウォークの実装例を以下に示す。
from numpy import *
from matplotlib.pyplot import *
from scipy import stats
def quantum_walk(N):
P = 2*N+1 # number of positions
coin0 = array([1, 0]) # |0>
coin1 = array([0, 1]) # |1>
C00 = outer(coin0, coin0) # |0><0|
C01 = outer(coin0, coin1) # |0><1|
C10 = outer(coin1, coin0) # |1><0|
C11 = outer(coin1, coin1) # |1><1|
C_hat = (C00 + C01 + C10 - C11)/sqrt(2.)
ShiftPlus = roll(eye(P), 1, axis=0)
ShiftMinus = roll(eye(P), -1, axis=0)
S_hat = kron(ShiftPlus, C00) + kron(ShiftMinus, C11)
U = S_hat.dot(kron(eye(P), C_hat))
posn0 = zeros(P)
posn0[N] = 1 # array indexing starts from 0, so index N is the central posn
psi0 = kron(posn0,(coin0+coin1*1j)/sqrt(2.))
psiN = linalg.matrix_power(U, N).dot(psi0)
prob = empty(P)
for k in range(P):
posn = zeros(P)
posn[k] = 1
M_hat_k = kron( outer(posn,posn), eye(2))
proj = M_hat_k.dot(psiN)
prob[k] = proj.dot(proj.conjugate()).real
return prob, P
N = 100
prob ,P = quantum_walk(N)
fig = figure()
ax = fig.add_subplot(111)
plot(arange(P), prob)
show()
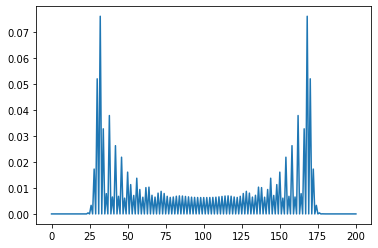
ゴール位置の確率分布を以下に示す。
ランダムウォークでは、出発地点をピークに、正規分布を描くが、量子ウォークでは、二つのピークが現れる。
5.終わりに
・応用例として、時系列データ予測に使えることが示唆されているが、応用例にそった実装例がない。今後は、応用例の実装例を共有したい。
更新履歴
Rev.0 2020/12/6 新規作成