数学とプログラミング(どうでもいい前書き)
この記事は NCC Advent Calendar 2017 の24日目の記事です。
ちなみに今は12月24日、クリスマスイブの朝1時ごろです!爆速で今から書き上げるのです!
Lineの背景に雪が降り始めましたが、特にそうなる兆しもなく、でも今日の夜は雨になるみたいな予報を電車の中で見ました。書き始めます。適当なテンションで書いているので、日本語はかなりデタラメです。イッチバン下にある、作成した作品の例をチラッと見ていただくだけでもいいので、楽しんでいってください!
はじめに
こんにちは、まずは、アクセスしていただきありがとうございますm(_ _)m
季節の挨拶みたいに、適当な前書きから始めたいと思います。ご迷惑でしたらすっ飛ばしてください。
ネットの記事だったり技術書だったり、ちまたでは「数学なんていらない!!簡単プログラミング!アプリ開発!」といった文言をたくさん見かけますね。すごく煽り口調で書いてしまったのですが、特に否定をしているわけではありません。誰でもプログラミングをできるようになって、作りたいものを作れるようになるのは素晴らしいことです。
ですが、プログラミングで自分の作りたいものを、表現したいものを創る時には複雑なアルゴリズムや設計が求められることは少なくありません。そういう時に求められるのはやはり数学だと思います。
まあ、そんなことは誰でも分かってるんです。
- 「機械学習をやりたい!入門だけでも!!」と思って本屋に行ったら
行列・微積・統計のさんコンボの1発KOを食らった人も少なくないと思います。 - たまたま開いたアルゴリズムの本に$ \sum $が出てきて、脳卒中で倒れてしまった方もいるのではないでしょうか...?
でもでもでも、こういう難しい計算をしてくれるものは、たくさんの世界の頭がいい強い人が作ってくれています。そのおかげで、みんな怖いよ機械学習ちゃんだって簡単なものならば
- 2次元配列をちょちょいと用意する
- データを読み込む
- 用意された関数に投げる
- 結果を表示する
という、たかだか4つくらいのステップでできてしまいます。
Artになるとさ...
複雑な計算をして、それをソフトウェアのViewに表示させたい時くらいはいいんです。こうやって誰かが用意してくれたものを使えばfloat型かなんやらの結果が返ってくるんです。車輪の再発明はしなくて良いように世界が頑張ってるんです。
しかし、それがメディアアートになるとどうでしょうか...? 個人的にですが、メディアアートを作っているとソフトウェアを作るよりも細かいことを求めてしまうんですね。そういう時、既存のものではなんだか満足できない時があります。そういうのは、大抵、 計算するというよりは アルゴリズムを組み立てなきゃいけない内容に現れてきます。
ところで、このNCC Advent Calendarに先輩たちが個人的に心にくる記事を書いてくださいました。
この二つなんですが、分野としては、画像処理と幾何学ですね...
ちょっとここに便乗するとして、幾何学のアルゴリズムを頑張って組み立てて、画像加工に利用した遊びを紹介したと思います
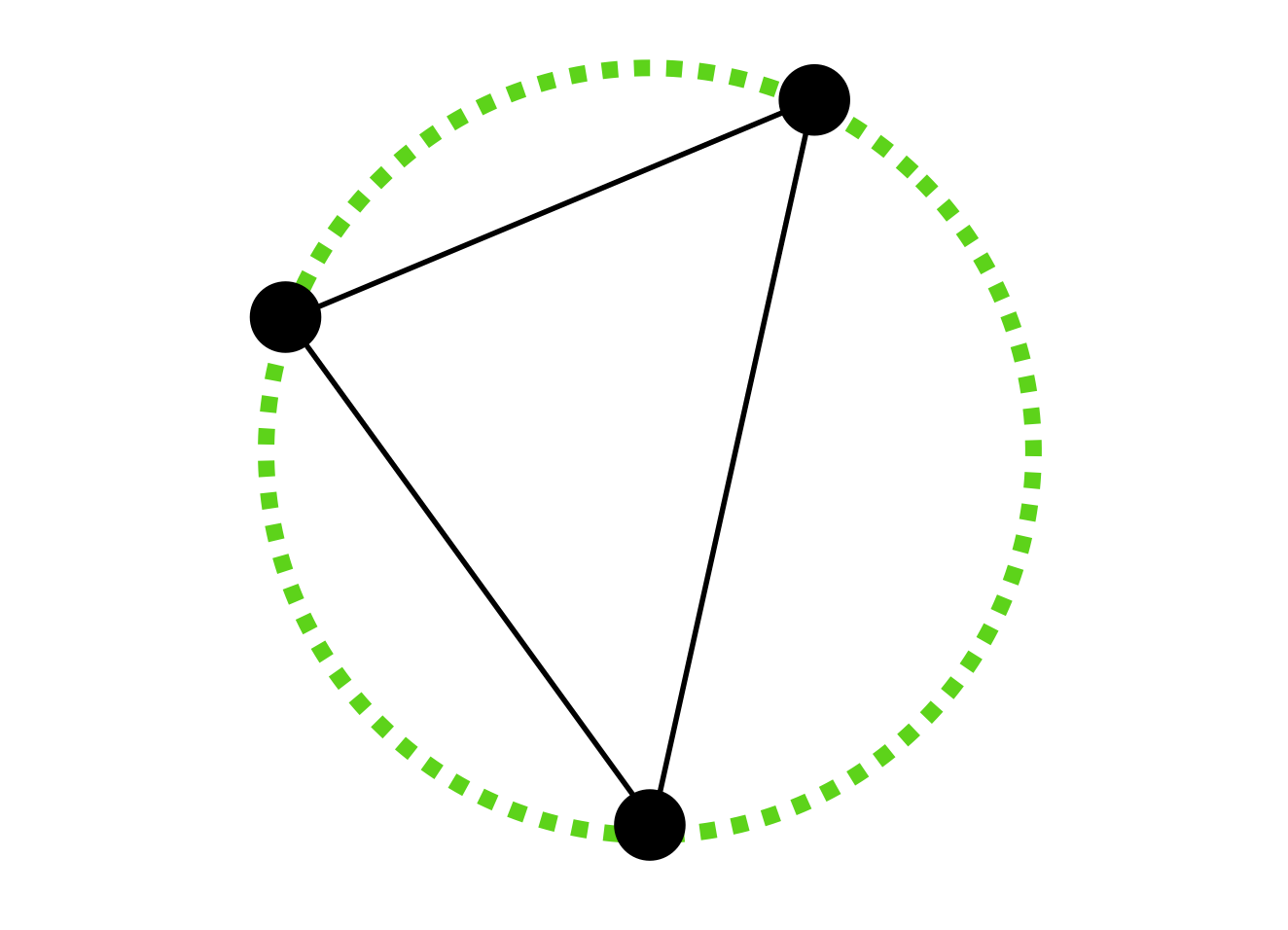
「外接円」覚えてる...?
三角形の外接円は上みたいな感じです。さてさてこれから数式と遊んでいきましょう!
これから、(三角形の外接)円にまつわる公式を2つ紹介します。
正弦定理
$$ 2R = \frac{a}{sinA} $$
みたいな色は覚えていますか...?
三角形の角から1つ選んでAとし、の対辺をa としてあげると、この公式が成り立ちます。
この式は使わないのですが、高校の時にみなさんならいましたよね...?いろんなことを思い出して欲しいので紹介しました笑
円の方程式
$$ (x-a)^2 + (y-b)^2 = r^2 $$
としてあげれば、この円は$(a,b)$が中心で$r$が半径の円となります。
もし、ユーザー(or 初期条件)から3つの座標情報が与えられているとしましょう。
そんな時にその3つの点でできる三角形の外接円の中心の座標と半径を求めてください!! って言われたら、すぐ求め方を答えられますか...?それをプログラミングで書きあらわせたらもっと良いですね!
こんな、数1とか数2で習った簡単な知識ですが、これから紹介するもののアルゴリズムにはバンバン使うので、確認して見ました!それでは本題に行きましょう!!!
Delaunay's Triangulation
なにそれ
かっこよく英語で書いてしまったのは本当にゴメンなさい。日本語で言えば 「ドロネーの三角形分割」
ちなみに
Triangulationという単語ですが
「三角測量」という意味で使われる方が多いみたいです...?
数学者のドロネーさんが考えたものなのですが、なんというか
空間を与えられた点を用いて、三角形で分割する
ものなんですね。まあ、言葉で言ってもあれなので...
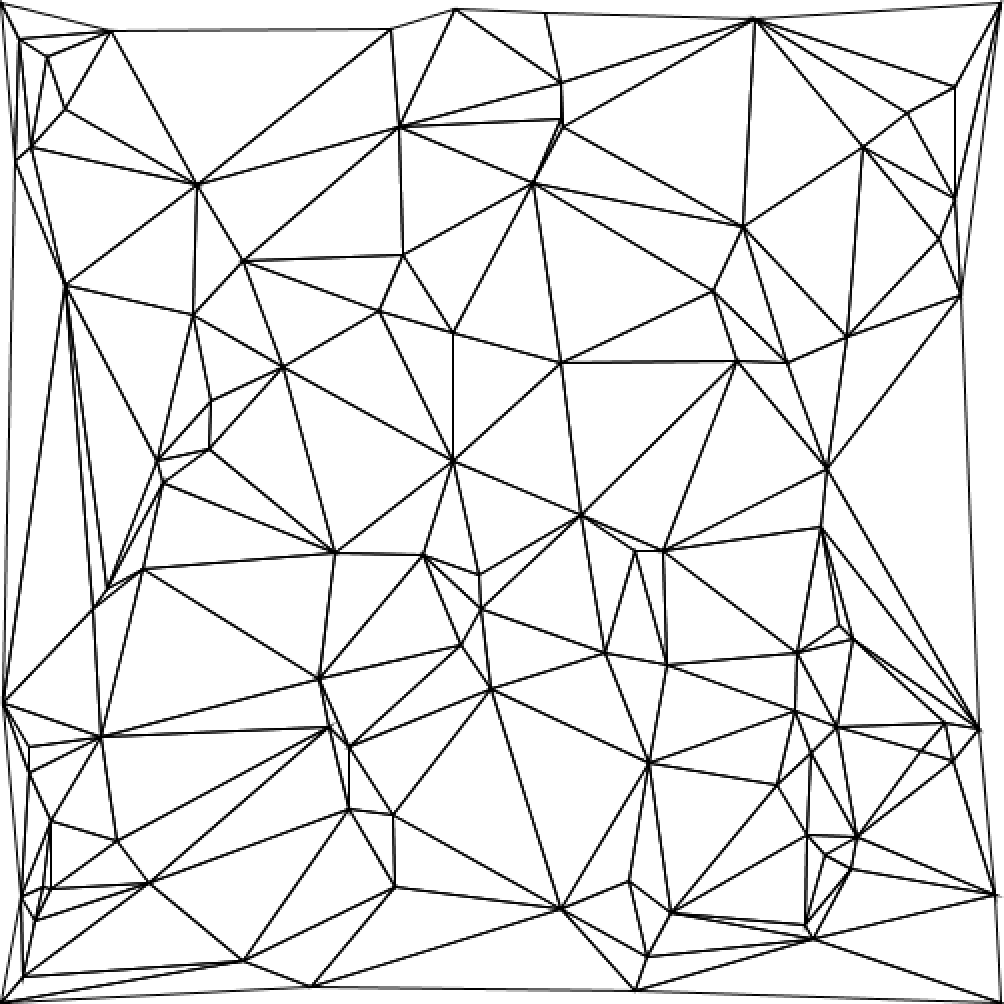
こんな感じに空間を三角形で分割したいんです。たくさんの与えられた点を使って三角形を作るのですが、ランダムに点を選んで結ぶわけにはいかないんです。とっても細長い三角形や、線と線が交差して、意図していない三角形ができてしまうかもしれません。そういう風に、「綺麗な三角形」で綺麗に分割していくのが、ドロネーの三角形分割です!
綺麗な三角形って...?
みなさんどんな三角形が綺麗だと思いますか...?
異論反論はとりあえずすっ飛ばして、一番綺麗な三角形は正三角形です。
なぜならば、正三角形はどこかの点が飛び出ているみたいなことは絶対にありません。
じゃあ沢山の三角形を空間内につくりたいな〜〜って時はどうしましょうか。目標としては、次のようなことを掲げます。
3つの内角の最小角度が最大になるような組み合わせを得る
正三角形はすべての角度が60度です。当たり前のことなのですが、三角形の最小角度は何があろうと60度を超えることはないです。だから、この目標のもとでは正三角形がもっとも綺麗な三角形となります。
これで伝わったらすごい、アルゴリズム紹介
さてさて、問題はこのアルゴリズムです。どうやったら上に貼った画像のように空間を三角形で分割できるのでしょうか...?
詳解OpenCV (←amazon)という本によれば、次のようなアルゴリズムで解けるといいます。
- とある点の集合すべてを含むような巨大な三角形を追加する
- 点集合のうち、i番目の点(Pi)を三角形分割図形に追加
(初期であれば、巨大三角形の中に集合の中のどれかの点を入れるところから開始)- 点Piをその外接円に含む三角形ABCを見つけ、点Piを使ってその三角形を分割する
(ABPi,BCPi, CAPiの3つの三角形)
このとき、辺AB, BC, CAをスタックに積む。このスタックをSとする。 - スタックSが空になるまで以下を繰り返す
- スタックSの一番上の辺をpopし、これを次の辺ABとする
- 辺ABを含む2個の三角形をABC, ABDとする。
三角形ABCの外接円にDが含まれる場合は、辺Bをフリップし、辺AD/DB/BC/CAをスタックSにpushする
そうでないならば処理をスキップする
- 点Piをその外接円に含む三角形ABCを見つけ、点Piを使ってその三角形を分割する
- 最初に作成した、巨大三角形と、その頂点を1つでも含む三角形をすべて削除する
まだ、少しだけ、読みやすいようにしたつもりですが、さっぱりなんのことかわかりませんね...
特に「以下を繰り返す」という部分。どうみたってここが一番重要なのに、さっぱりわかりません。
頑張って、図とともに解説してみます...
まあ順番おってこうぜ
だんだん解説記事になってきましたね。実際にソースコードにするところまではいきませんが、順をおって頭の体操をしてみましょう!!
1. とある点の集合すべてを含むような巨大な三角形を追加する
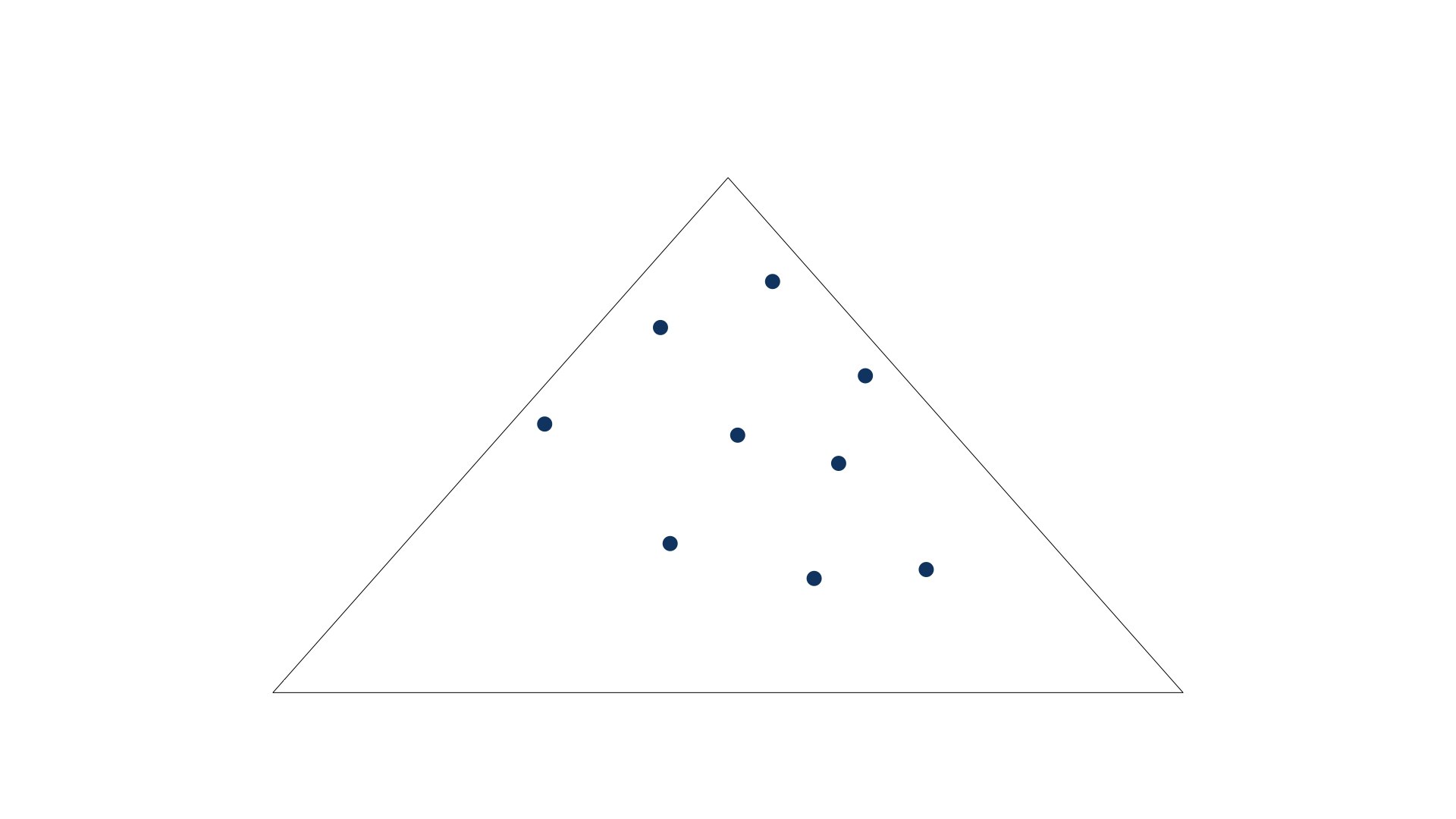
これは簡単です。このように、点の集合を用意してあげれば...
こんな風に巨大な三角形を作るっていうことです。
これで完成です!次に行きましょう!
2. 点集合のうち、i番目の点(Pi)を三角形分割図形に追加
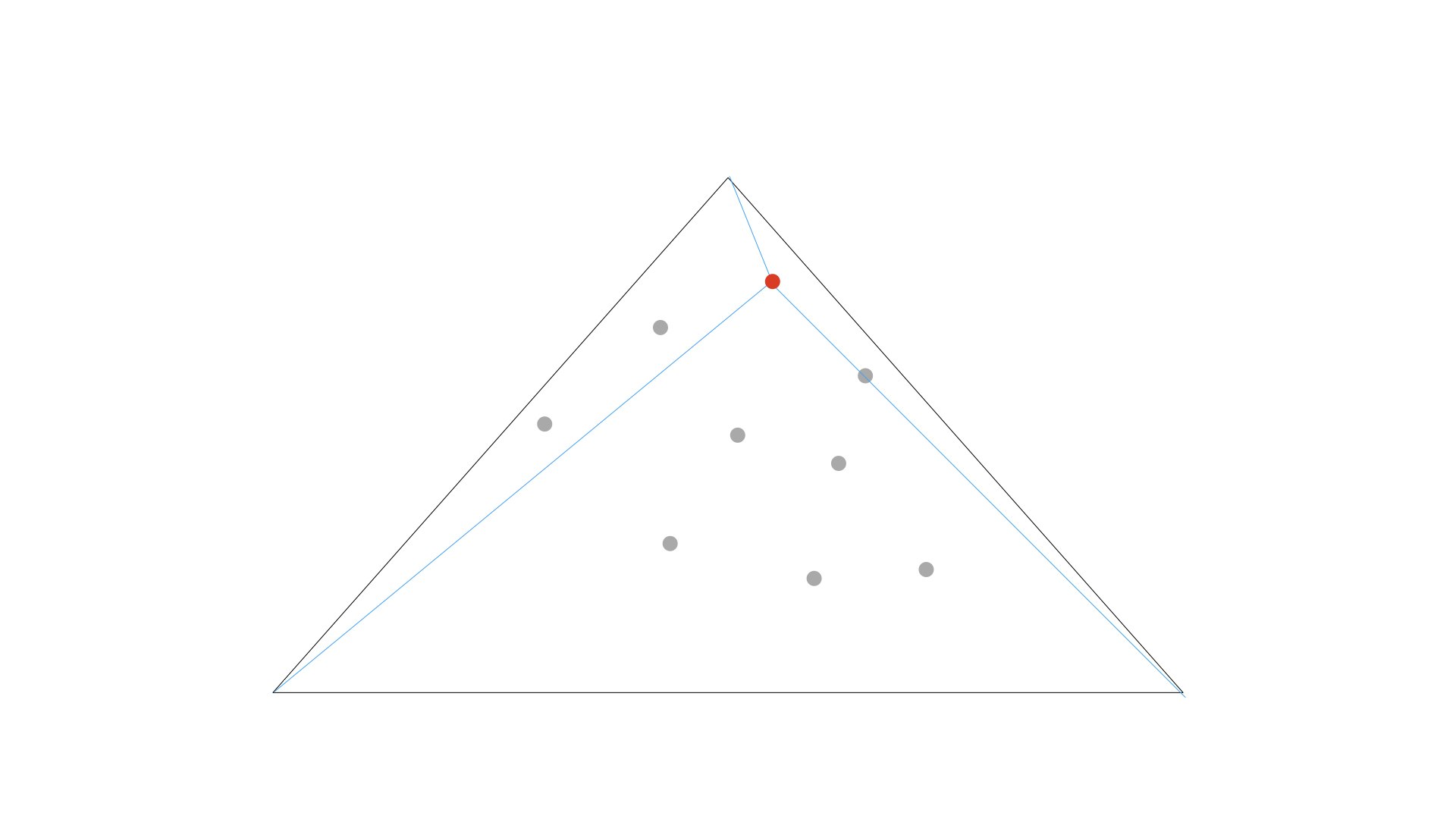
さっきの点の中から、一つ取り出して、追加しましょう!この三角形に対して、いくつか処理を行います!
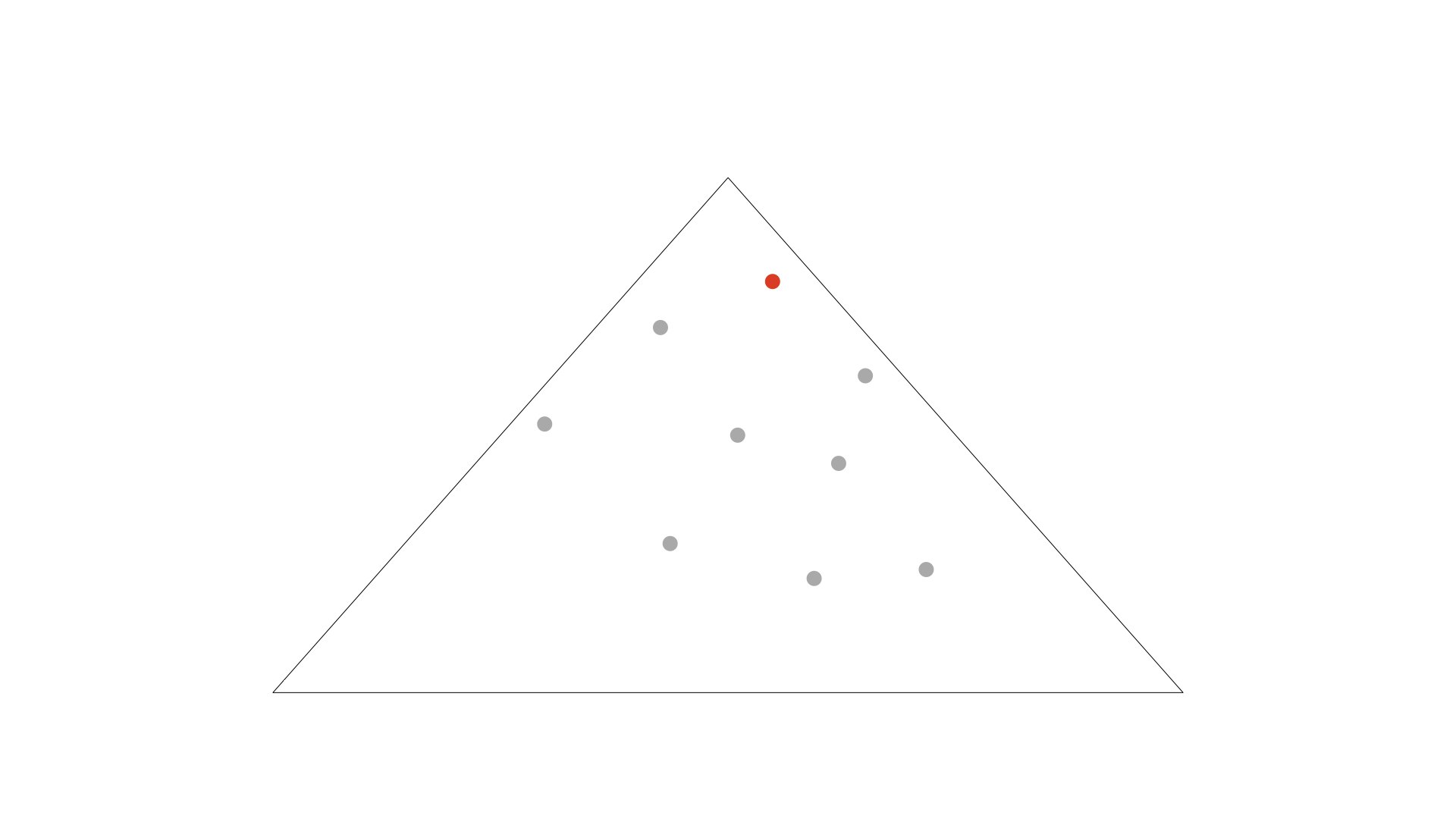
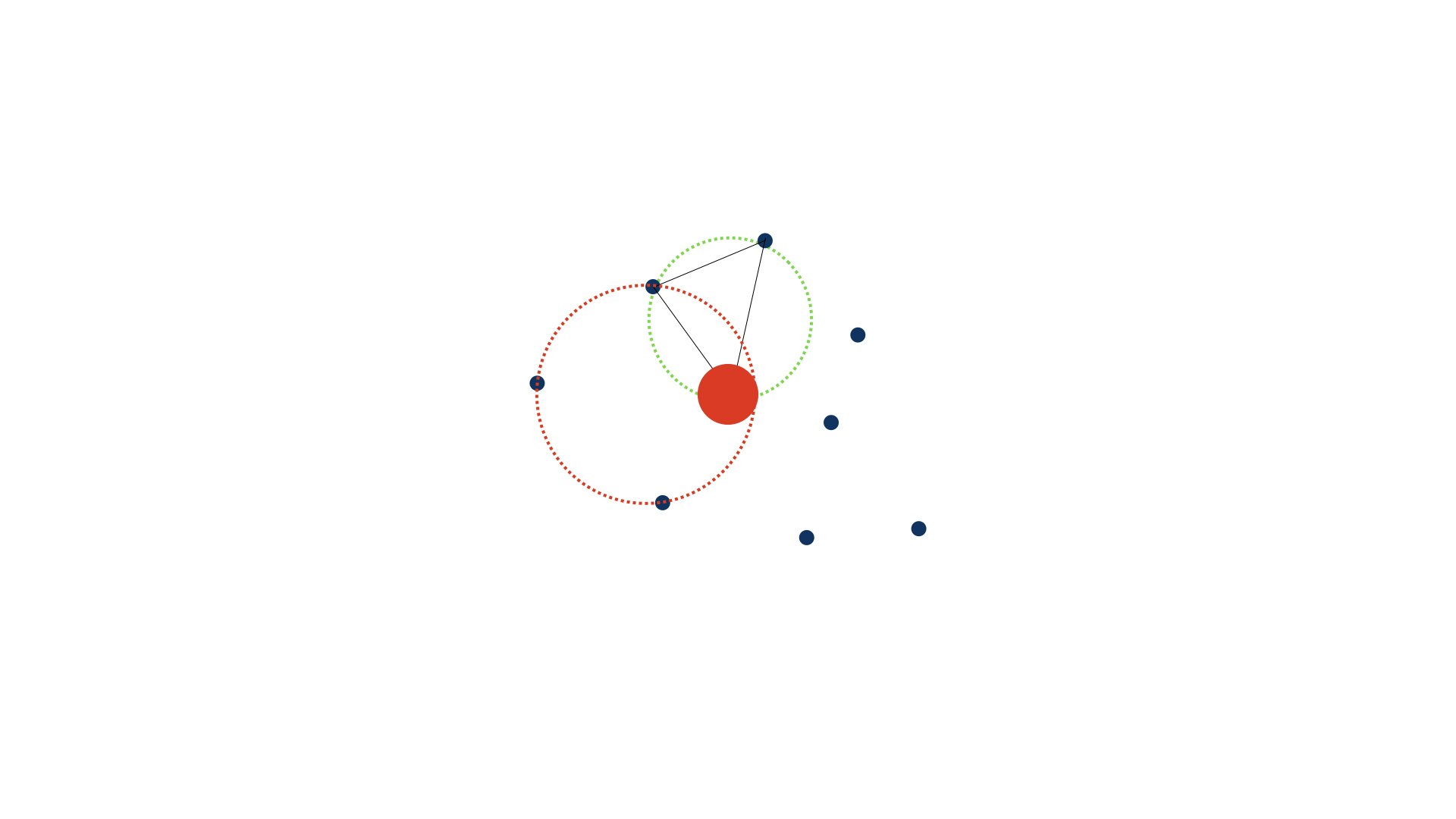
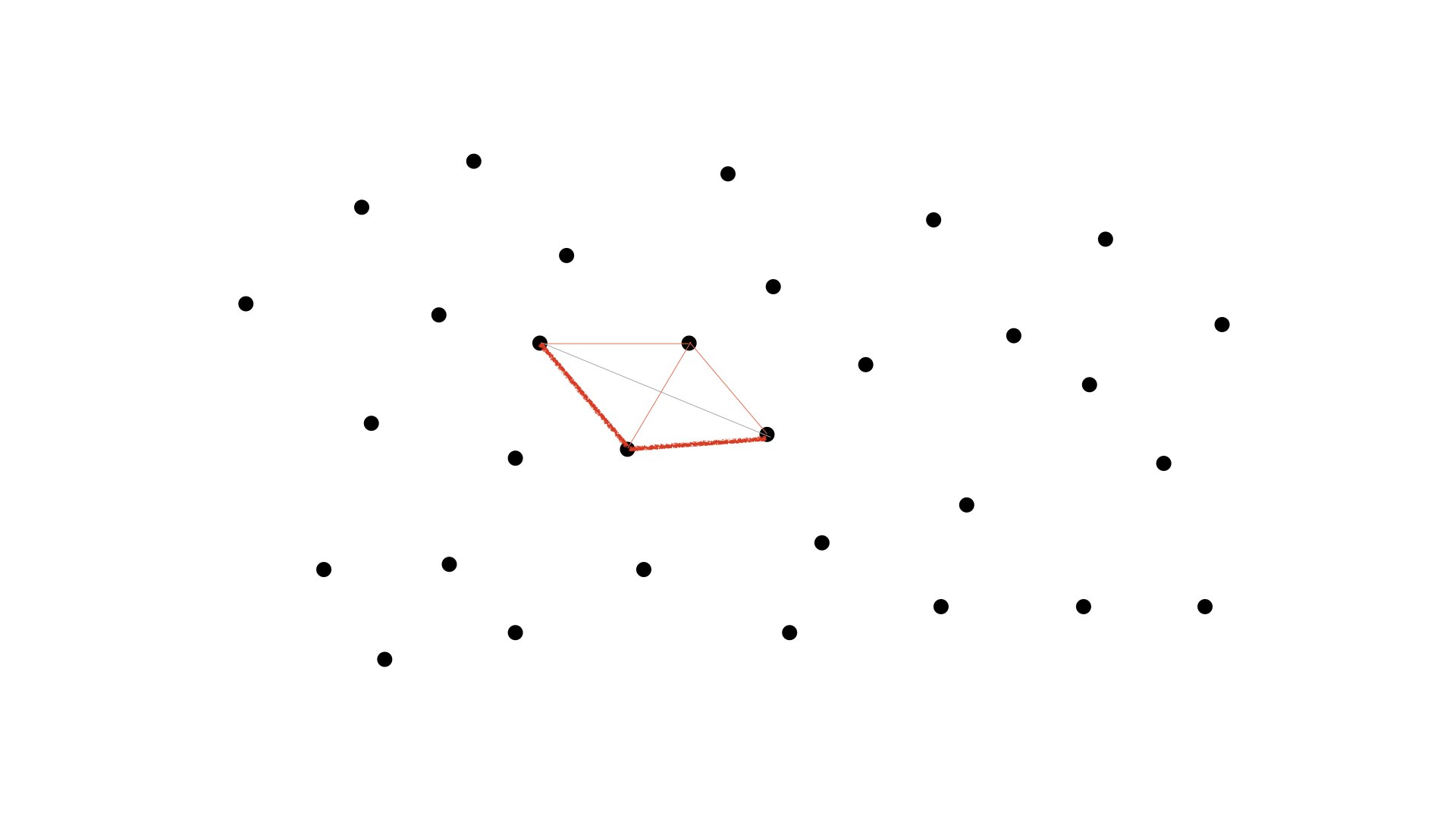
点Piをその外接円に含む三角形ABCを見つけ、点Piを使ってその三角形を分割する
さっき追加した赤い点は、最初に用意した巨大三角形外接円にの中に位置しますね。(さすがにこれは自明です)なので、この点を使って巨大三角形を分割したいと思います
このように水色の線を使って巨大三角形を分割し、新しい三角形を3つ作ります。
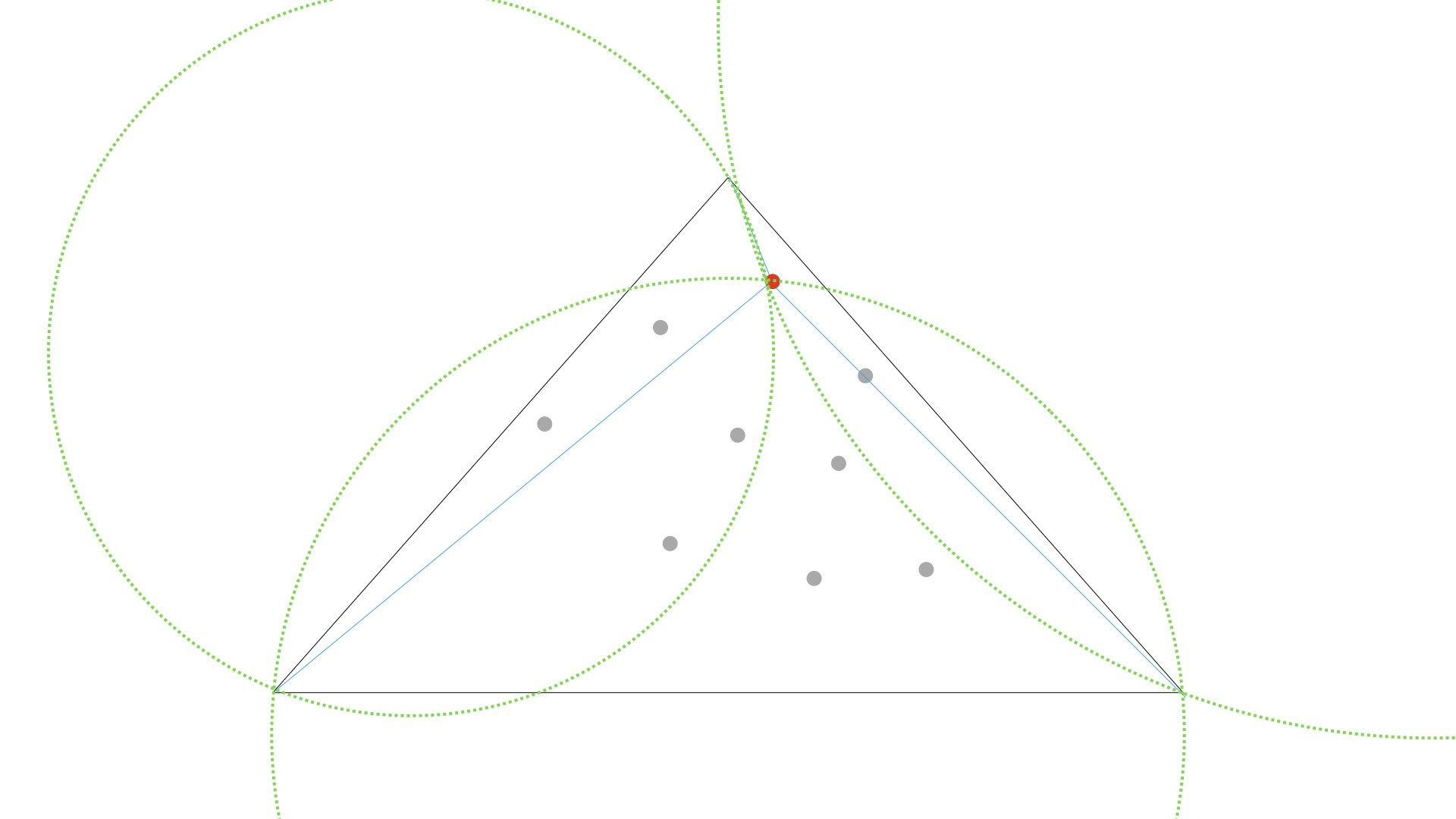
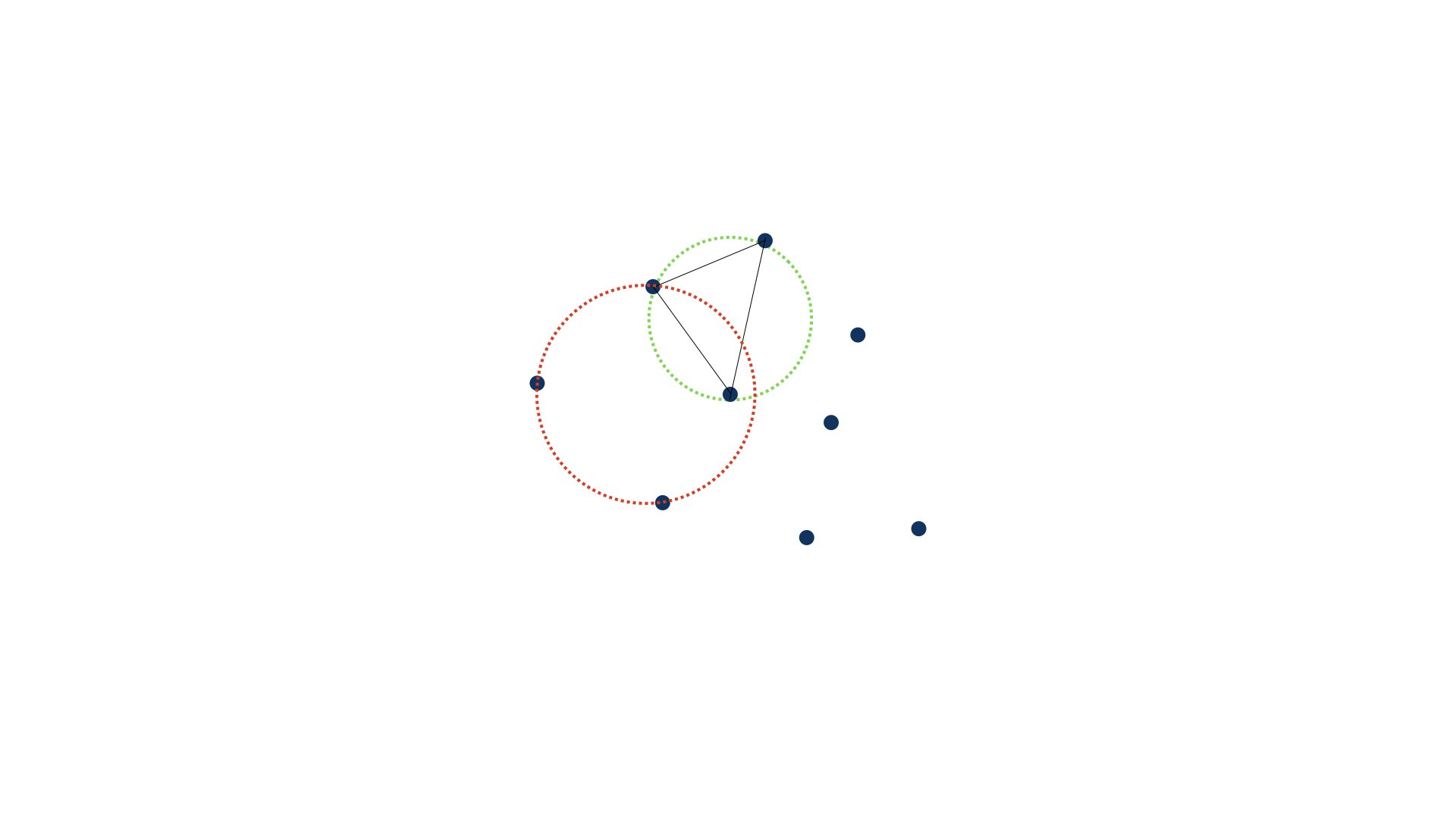
今分割した三角形について、それぞれの三角形の外接円を調べる
3つの三角形の外接円を書くと、このようになります
引いてみればこんな感じです。
今は、巨大三角形に点を追加して、3つの三角形に分割しました。この新たな3つの三角形すべてのが外接円をみてみると、それぞれの外接円に、他の三角形の頂点が含まれてはいなかったので、これで処理は終わりです。
次はまた2番を最初から繰り返します。
こんな感じに、分割したすべての三角形の外接円に、他の三角形の頂点が含まれないように、していくんです。これを外接円特性そうすると、綺麗に三角形分割ができます。
3. 最初に作成した、巨大三角形と、その頂点を1つでも含む三角形をすべて削除する
最初に作成した巨大三角形は、最初から三角形分割が予期せぬエラーなく実行できるように用意した、いわば初期条件で、任意の点での空間の分割にはあまり関わりはありません。なので、この巨大三角形とその三角形の頂点を含んだ三角形をすべて削除することをお勧めします。
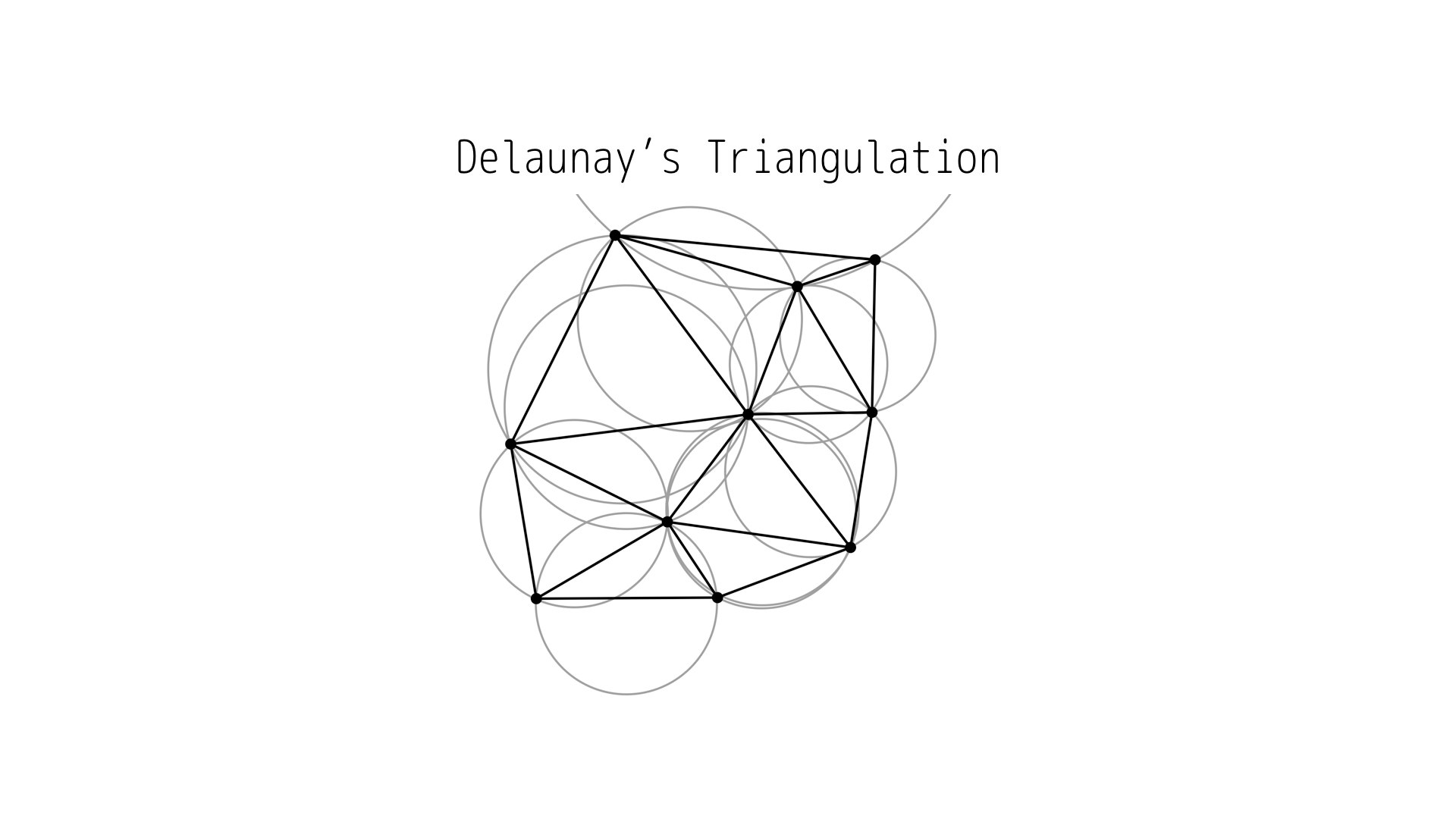
完成図
これは10個の点で三角形分割されています。また、それぞれの三角形の外接円も書かれています。
すべての外接円の中に、他の三角形の頂点が含まれていないことが、確認できたと思います...
ところで、今みたいにスルーーっといかないと...?
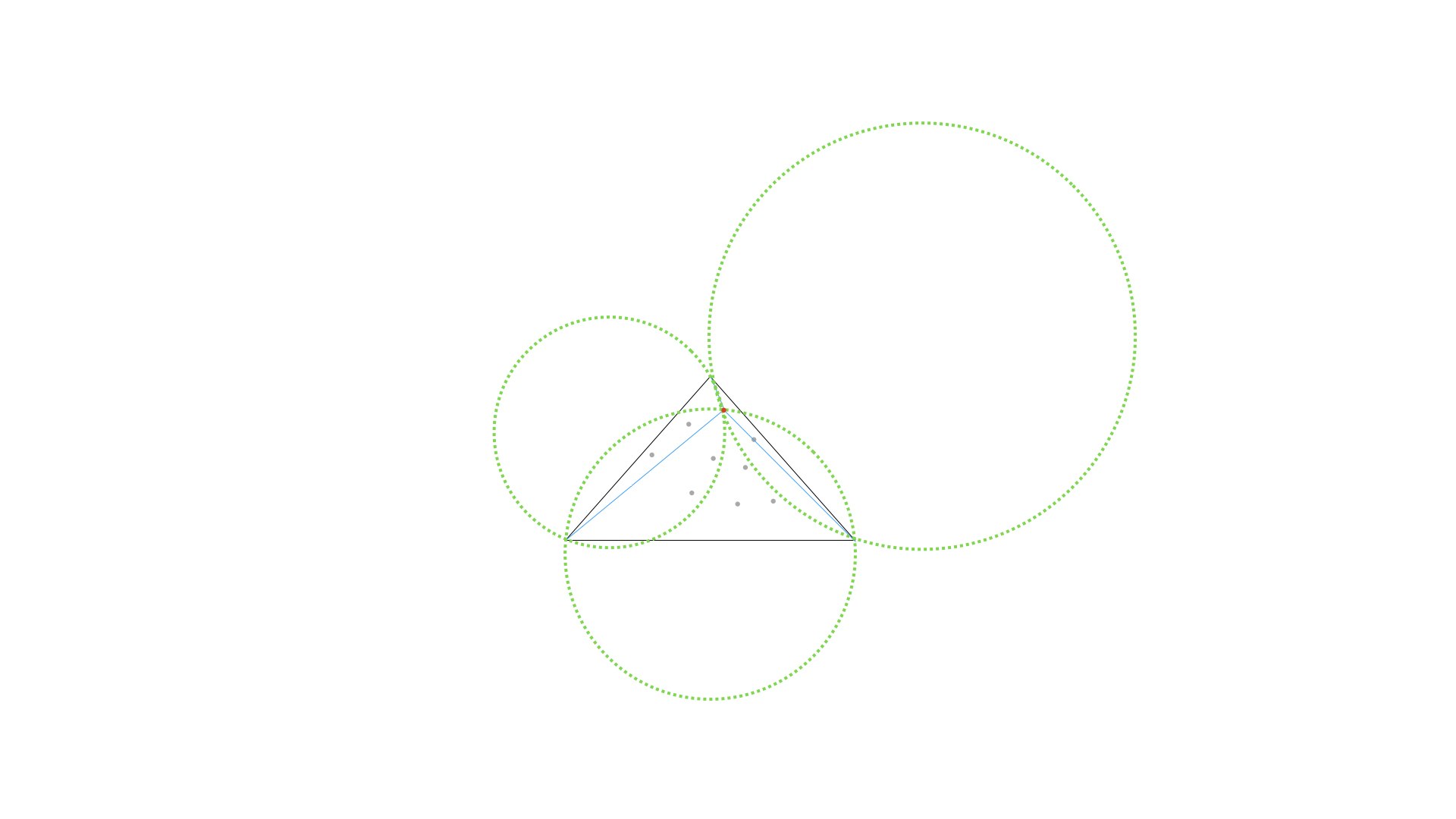
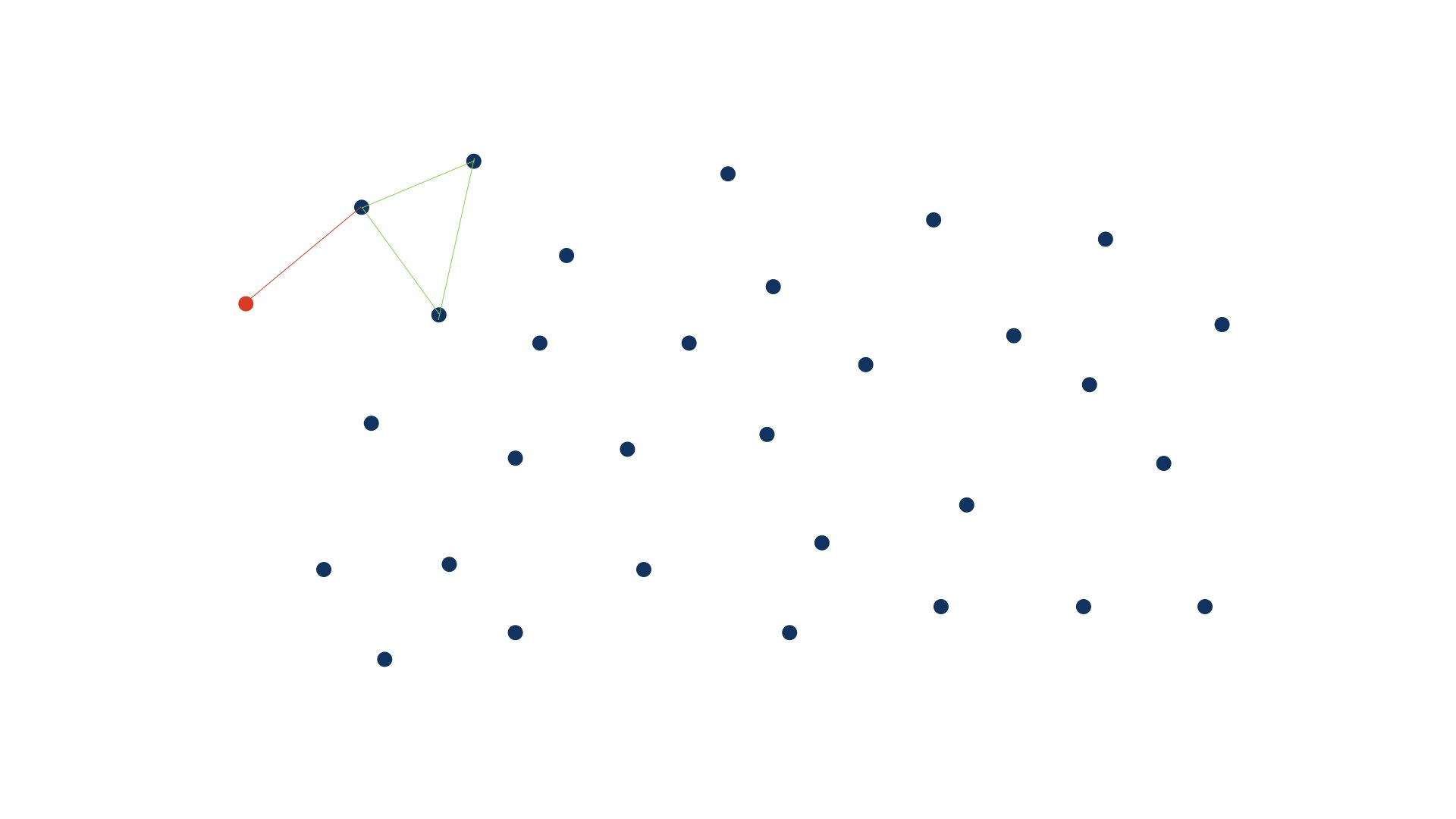
さっき、巨大三角形の中に一つだけ点を追加して、うまく分割することができました。しかし、そうはうまくいかない場合もあります。色々複雑な場合があるのですが、とりあえず理解を深めるために次の図について考えてみましょう。
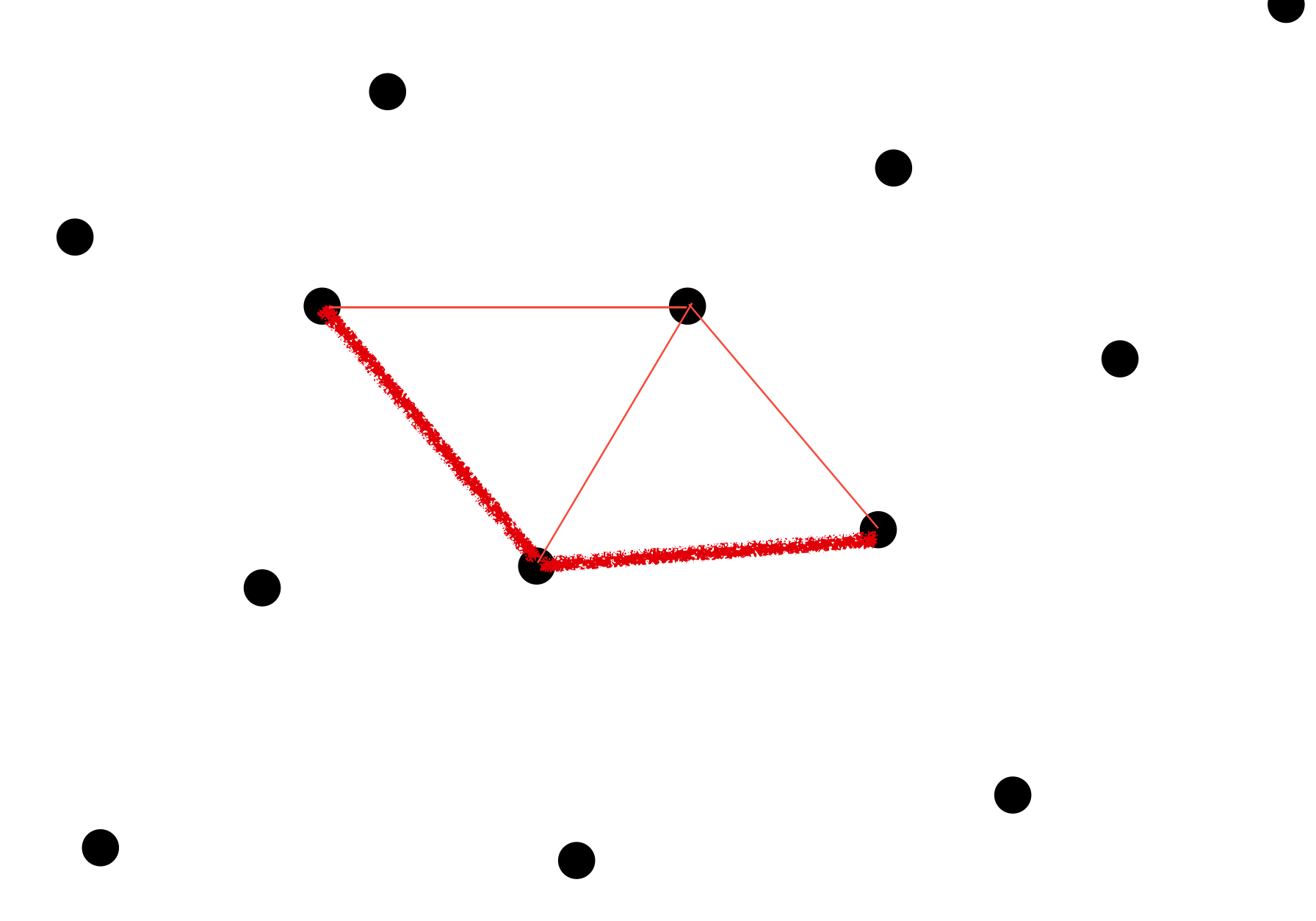
外接円で判定する①
- 黄緑色の辺の三角形の隣に赤い点を追加したとしましょう。
こうなった時に、更に次の画像のなかで
- 水色の点線
- 赤色の点線
どっちの線を使って三角形分割を行えばいいのでしょうか...?
これは簡単に水色の点線とわかるのですが、それを外接円を使って確認してみましょう。
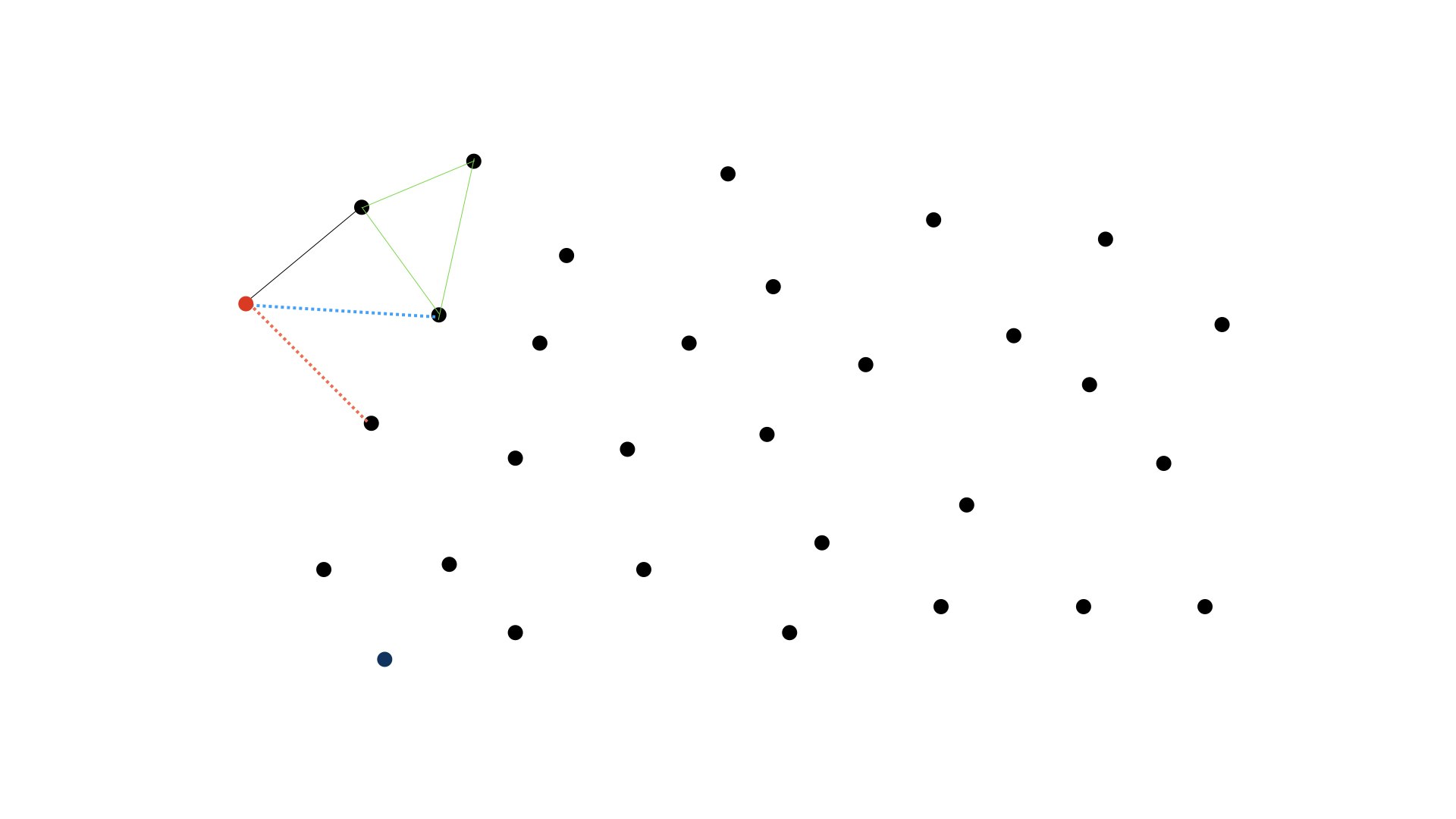
水色の点線を選んだ時(正解ルート)
水色の点線を選んだ時にできる三角形の外接円が、これまた水色の点線で書かれています。これをみれば、この外接円の中に、他の三角形の頂点が含まれていないので、これが正解とわかります。
赤色の点線を選んだ時(不正解ルート)
こんな感じの赤い点線の外接円が出来上がります。みれば簡単に気付いちゃいますね、ダメだ!!って
ご覧の通り、大きい赤い点が、赤い点線の外接円の中に位置しています。こうなっては、正しく分割できていないんです。さっきの水色の点線を選んだ方が綺麗に分割できるということが、外接円を使った判定だけで書くことができます!!
外接円で判定する②
もし、下のような図の状況に出会ったとします!
ですが、一つ点を追加すると、どうやって三角形に分割していいのかわからなくなってしまったのです。
ひし形みたいな形の中に、2つの直線が交わっています。その2つの直線のうち、どっちの直線を使って三角形に分割した方が、綺麗な三角形になるのでしょうか....? これもさっきの問題と考え方は同じで、どっちかの線を選べば、そこにあるすべての三角形の外接円は、他の三角形の頂点を含んでいない人がよくよくわかります!!
なんなら、この図を見て見ましょう。明らかに、さっきの三角形より正三角形に近い形で分割できているように思えます。
Delaunayを使って遊びたかった。
さて、そもそも自分がDelaunay's Triangulationにハマった理由なんですが、Photoshopでも作れるような三角形のポリゴン絵を作りたかったんです。PhotoshopとIllustratorで画像をポリゴン風に加工する方法 の記事みたいな感じです。こういう加工がとても好きなので、ちょいとプログラムでもやってみたいなと思って始めました。なので、簡単なアプリケーションみたいなものも作ったのでそちらを紹介します。
やったことは次のことです
- 画像を読み込む
- 1000*1000ピクセルの空間を用意し、その中に含まれる任意の点でDelaunay's Triangulationを行う
- 分割し終わった三角形すべてを描画する
- その際、三角形の重心の座標を求め、そこに対応する画像の色で三角形を塗りつぶす
そうすると...
この画像が、
こんな感じになります。
結構ありな感じだと思うんですよね。
他の作品としては、、、
こんな感じです。すっかり気に入ってしまって、LineとインスタグラムとTwitterのほぼすべてのアカウントを、このポリゴンで分割した画像にしてしまいました...!
おわりに!
さて、深夜テンションも大詰めです。なかなか辛くて、何を書いているのかほぼわかっていませんが、多分大丈夫です!クリスマスイブにふさわしい、ある程度の分量の記事を投げつけられたと思います!!寝ます!
外部リンク
いくつか、参考に見ていただけたらなあ〜といのがあります!
-
自分のGithub
- DelaunayTriangulation というクラスがこのアルゴリズムを実装しています
- ProcessingでDelaunay分割(解説篇)
-
ProcessingでDelaunay分割(実装篇)
- いくつか挙動が不審なところがあったので、自分のgithubの方で書き換えたり、好みな仕様にしていたりします