信号の時間-周波数解析の代表的な手法の1つである、連続ウェーブレット変換を勉強していたのですが、実際にプログラミングで実装するためには離散化しなければなりません¹。
ググると離散化した後の数式も見つかったのですが、イマイチよく分からなかったので自分で導出して、さらに実装してみました。

主に参考としたのは、I. Daubechies著の「ウェーブレット10講」（丸善出版）です。
かなりしっかりした理論の本ですが、ざっと読んだだけだと途中から訳わかめだったので、時間を取ってじっくり読み直したいです。

連続ウェーブレット変換の定義

連続ウェーブレット変換の背景やらは色んなところに載っているのでここでは割愛します。時間信号$x(t)$の連続ウェーブレット変換の式は以下の通り。

X(a, b) = \int_{-\infty}^{\infty} x(t)\,\overline{\psi}_{a, b}(t)\,dt \tag{1.1}

\psi_{a, b}(t) = \frac{1}{\sqrt{a}}\,\psi\Bigl(\frac{t - b}{a}\Bigr) \tag{1.2}

ここで、$\psi(t)$はマザーウェーブレット、$a$はスケール、$b$は時間シフトです。$\overline{\psi}$は$\psi$の複素共役を表します。
スケール$a$は周波数$f$の逆数に相当し、補正係数$\lambda$を用いて以下のように表せます。

a = \frac{\lambda}{f}\tag{1.3}

一方で、連続ウェーブレット変換の逆変換は以下の通り。

x(t) = \frac{1}{C_{\psi}}\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} X(a, b) \,\psi_{a, b}(t)\,db\,\frac{da}{a^2} \tag{1.4}

$C_{\psi}$はadmissible constantと呼ばれる数で、この値が有限であることが逆変換の存在条件になっています。

C_{\psi} = 2\pi\int_{-\infty}^{\infty}\frac{|\hat{\psi}(\omega)|^2}{|\omega|}d\omega<\infty \tag{1.5}

ここで、$\hat{\psi}(\omega)$はマザーウェーブレット$\psi(t)$のフーリエ変換です。

実用上、時間信号$x(t)$は実数である場合がほとんどで、この場合は(1.4)式を以下のように変形できるようです。

x(t) = \frac{2}{C_{\psi}}\int_{0}^{\infty} \int_{-\infty}^{\infty} X(a, b) \,\psi_{a, b}(t)\,db\,\frac{da}{a^2} \tag{1.6}

文献によって、(1.5)式の係数の$2\pi$が無かったり²、(1.6)式の係数に$2$が出てこなかったり、記述がバラバラですごく混乱しました…
今回は(1.1)式と(1.6)式を離散化していきます。

連続ウェーブレット変換の離散化

時間の離散化

連続ウェーブレット変換を離散信号に適用するためには、時間$t$に関する積分が邪魔なので、時間$t$を離散化していきます。
サンプリング周波数を$f_{s}$として、次式を満たす実数$n$を定めます。

\begin{align}
t &= \frac{n}{f_{s}}\\
&= n\Delta t\tag{2.1.1}
\end{align}

積分変数の置換のために微分しときます。

\frac{dt}{dn} = \Delta t \tag{2.1.2}

この時、時間信号$x(t)$をサンプリングした信号$x[n]$は以下のように表せます。

x[n] = x\Bigl(\lfloor\frac{t}{\Delta t}\rfloor \Delta t \Bigr) \tag{2.1.3}

ここでウェーブレットも離散化しておきます。

\psi_{a, b}[n] = \psi_{a, b}(n\Delta t) = \psi_{a, b}\Bigl(\lfloor\frac{t}{\Delta t}\rfloor \Delta t \Bigr) \tag{2.1.4}

(2.1.1)-(2.1.4)式より、(1.1)式は以下のように近似できます。

\begin{align}
X(a, b) &= \int_{-\infty}^{\infty} x[n]\,\overline{\psi}_{a, b}[n]\,\Delta t\,dn\\
&= \Delta t\sum_{n=-\infty}^{\infty} x[n]\,\overline{\psi}_{a, b}[n]\tag{2.1.5}
\end{align}

これで離散信号に対応させることができました。丁寧に書きましたがこれくらいは簡単ですね。

連続ウェーブレット逆変換の離散化

次に逆変換を離散化していきます。こっちが曲者でした。
とりあえず逆変換の式を再掲。

x(t) = \frac{2}{C_{\psi}}\int_{0}^{\infty} \int_{-\infty}^{\infty} X(a, b) \,\psi_{a, b}(t)\,db\,\frac{da}{a^2} \tag{1.6}

(2.1.3)(2.1.4)式を適用すると以下のようになります。

x[n] = \frac{2}{C_{\psi}}\int_{0}^{\infty} \int_{-\infty}^{\infty} X(a, b) \,\psi_{a, b}[n]\,db\,\frac{da}{a^2} \tag{3.1}

時間シフトの離散化

まずは時間シフト$b$の離散化です。
後々の計算のしやすさ等を考えて、時間$t$の離散化と同様に、サンプリング周期$\Delta t$を使って離散化します。具体的には以下の式を満たす実数$m$で表します。

b = m \Delta t \tag{3.1.1}

同じように微分しときます。

\frac{db}{dm} = \Delta t \tag{3.1.2}

(3.1.1)(3.1.2)式を(3.1)式に適用してみましょう。

\begin{align}
x[n] &= \frac{2}{C_{\psi}}\int_{0}^{\infty} \int_{-\infty}^{\infty} X(a, m\Delta t) \,\psi_{a, m\Delta t}[n]\,\Delta t\,dm\,\frac{da}{a^2}\\
&= \frac{2\Delta t}{C_{\psi}}\int_{0}^{\infty} \sum_{m=-\infty}^{\infty} X(a, m\Delta t) \,\psi_{a, m\Delta t}[n]\,\frac{da}{a^2} \tag{3.1.3}
\end{align}

とりあえずこれで時間シフト$b$の離散化は終わりです。

スケールの離散化

次はスケール$a$の離散化です。
時間$t$や時間シフト$b$の離散化は、信号自体をサンプリングしたものと考えればすんなりと出せるのですが、スケール$a$は特に決まりがないので、取り方によってはかなり粗い近似になってしまいます。その辺の妥当性については長くなりそうなので別記事へ。（2019/08/31 書きました→続: 連続ウェーブレット変換を使ってみたかったので離散化して実装した）

離散化の考え方ですが、(1.3)式の周波数$f$に対して、以下のように実数$l$を定めると逆変換の式が綺麗になって嬉しいです。

f = f_{0}\cdot2^{\frac{l}{l_{0}}} \tag{3.2.1}

周波数をオクターブ単位で表現しただけです。ここで$f_{0}$は基準周波数で、$l_{0}$はオクターブ分解能です。
例えば、$f_{0}$を440Hz、$l_{0}$を12とすれば、整数$l$に対し、周波数$f$はピアノの各鍵盤の音の高さ（12平均律）を表します。楽曲の解析にちょうど良い。

(1.3)式より、スケール$a$は以下のように表せます。

a = a_{l} = \frac{\lambda}{f_{0}} \cdot 2^{-\frac{l}{l_{0}}} \tag{3.2.2}

またまた微分しときます。

\begin{align}
\frac{da}{dl} &= \frac{\lambda}{f_{0}} \cdot 2^{-\frac{l}{l_{0}}} \cdot \Bigl(-\frac{\ln 2}{l_{0}}\Bigr)\\
&= -\frac{a\ln 2}{l_{0}} \tag{3.2.3}
\end{align}

(3.2.2)(3.2.3)式より、(3.1.3)式は以下のように変形できます。

\begin{align}
x[n] &= \frac{2\Delta t}{C_{\psi}}\int_{\infty}^{-\infty} \sum_{m=-\infty}^{\infty} X(a_{l}, m\Delta t) \,\psi_{a_{l}, m\Delta t}[n]\, \Bigl(-\frac{a_{l}\ln 2}{l_{0}}\Bigr) \frac{dl}{a_{l}^2}\\
&= \frac{2\ln 2 \cdot \Delta t}{C_{\psi}l_{0}}\int_{-\infty}^{\infty} \frac{1}{a_{l}} \sum_{m=-\infty}^{\infty} X(a_{l}, m\Delta t) \,\psi_{a_{l}, m\Delta t}[n]\,dl\\
&\approx \frac{2\ln 2 \cdot \Delta t}{C_{\psi}l_{0}}\sum_{l=-\infty}^{\infty} \frac{1}{a_{l}} \sum_{m=-\infty}^{\infty} X[l, m] \,\psi_{l, m}[n] \tag{3.2.5}
\end{align}

最後の行で$X(a_{l}, m\Delta t)$を$X[l, m]$、$\psi_{a_{l}, m\Delta t}[n]$を$\psi_{l, m}[n]$と書き直しました。これでスケール$a$の離散化終わりです。

周波数$f$を対数で取ってあげると綺麗になりますね。音声に適用すれば実用性も兼ね備えて良い感じです。
周波数$f$を線形に取る場合でも、同じように積分変数の置換をしてあげればできるはず³。

導出のまとめ

整数$l, m, n$を用いて、周波数$f$、スケール$a$、時間シフト$b$、時間$t$を以下のように離散化しました。

f = f_{0}\cdot2^{\frac{l}{l_{0}}}

a = \frac{\lambda}{f}

b = m \Delta t

t = n\Delta t

この時、連続ウェーブレット変換および逆変換は以下のように離散化できます。

X[l, m] = \Delta t\sum_{n=-\infty}^{\infty} x[n]\,\overline{\psi}_{l, m}[n] \tag{4.1}

x[n] = \frac{2\ln 2 \cdot \Delta t}{C_{\psi}l_{0}}\sum_{l=-\infty}^{\infty} \frac{1}{a_{l}} \sum_{m=-\infty}^{\infty} X[l, m] \,\psi_{l, m}[n] \tag{4.2}

Pythonで実装

数式を導出できたので実装していきましょう。言語はpython3です。
そもそも、Pythonで連続ウェーブレット変換と逆変換を手軽に扱えるモジュールが見つからなくて、それなら自作してやる！ってのがこの記事の始まりだったりします。
コード全文はGitHubに上げています。

マザーウェーブレットの実装

マザーウェーブレットは色んな関数がありますが、今回は以下の式で表されるMorletウェーブレットと呼ばれる関数を使います。

\psi(t) = \frac{C_{\omega_{0}}}{\pi^{1/4}}e^{-\frac{1}{2}t^2}\,(e^{j\omega_{0}t} - e^{-\frac{1}{2}\omega_{0}^2}) \tag{5.1.1}

ここで$C_{\omega_{0}}$は以下の式で表されます。

C_{\omega_{0}} = \Bigl(1 + e^{-\omega_{0}^2} - 2e^{-\frac{3}{4}\omega_{0}^2}\Bigr)^{-\frac{1}{2}} \tag{5.1.2}

それではMorletクラスを実装していきましょう。__init__メソッドはこんな感じ。

Morlet.py

import numpy as np

class Morlet(object):
    def __init__(self, w0=6.0):
        self.w0 = w0
        self.Cw = (1 + np.exp(-self.w0 ** 2) - 2 * np.exp(-0.75 * self.w0 ** 2)) ** (-0.5)
        self.C = self._get_C() # admissible constant

admissible constantの計算

admissible constantの計算部分のコードは以下の通り。

Morlet.py

    def _get_C(self):
        # calc admissible constant
        wmax = 1000
        dw = 0.01
        w = np.arange(-wmax, wmax + 1, dw)
        Wf = self._get_W_fourier(w)
        C = 2 * np.pi * dw * np.sum(np.abs(Wf) ** 2 / np.abs(w))
        return C

    def _get_W_fourier(self, w):
        # calc fourier transform of wavelet
        k = np.exp(-0.5 * self.w0 ** 2)
        Wf = self.Cw / np.pi ** 0.25 *\
            (np.exp(-0.5 * (w - self.w0) ** 2) - k * np.exp(-0.5 * w ** 2))
        return Wf

admissible constantは(1.5)式で表されます。

C_{\psi} = 2\pi\int_{-\infty}^{\infty}\frac{|\hat{\psi}(\omega)|^2}{|\omega|}d\omega<\infty \tag{1.5}

解析解を求めることが難しいので、近似解を求めます。
Morletウェーブレットのフーリエ変換は以下のように表せます。

\hat{\psi}(\omega) = \frac{C_{\omega_{0}}}{\pi^{1/4}} \bigl(e^{-\frac{1}{2}(\omega - \omega_{0})^2} - e^{-\frac{1}{2}(\omega^2 + \omega_{0}^2)} \bigr) \tag{5.1.3}

(1.5)式の被積分関数をプロットしてみると下図のようになります。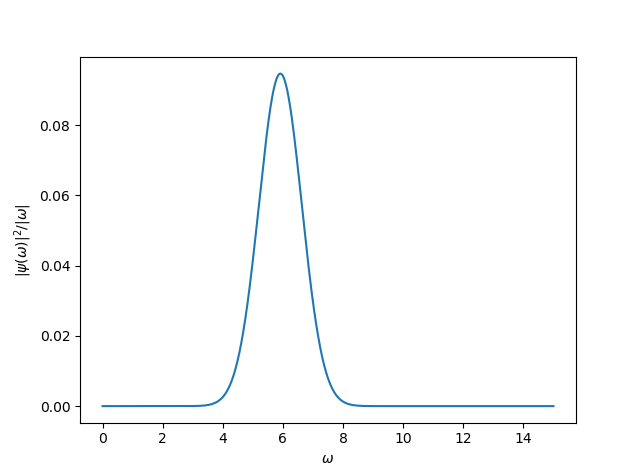
今回は積分範囲を$-1000\leqq\omega\leqq1000$としましたが、もっと狭くても大丈夫そうですね。

スケールの計算

周波数からスケールへの変換は(1.3)式で求められます。

a = \frac{\lambda}{f}\tag{1.3}

スケール$a$に対し、ウェーブレット$\psi(\frac{t}{a})$のフーリエ変換は$a\,\hat{\psi}(a\omega)$となります。このピークを取る角周波数$\omega_{c}$がスケール$a$に対応する角周波数と見なせます。よって、スケール$a$に対応する各周波数$\omega$は以下の式を満たします。

a\omega = \omega_{c} \tag{5.1.4}

ここで、$\omega_{c}$は以下の式の解となります⁴。

\omega_{c} = \frac{\omega_{0}}{1 - e^{-\omega_{0}\omega_{c}}} \tag{5.1.5}

逆に周波数$f$に対応するスケール$a$は(5.1.4)式を変形することで求められます。

a = \frac{\omega_{c}}{\omega} = \frac{\omega_{c}}{2\pi f} \tag{5.1.6}

よって、(1.3)式の補正係数$\lambda$は次式で表せます。

\lambda = \frac{\omega_{c}}{2\pi}

コードに起こすとこんな感じ。

Morlet.py

    def freq2scale(self, freq):
        # calc scales from frequencies.
        # center freq wf is given by the solution of below:
        #   wf = w0 / (1 - exp(-wf * w0))
        # if w0 > 5, wf is nearly equal to w0.

        w_center = self.w0
        for i in range(100):
            w = w_center
            w_center = self.w0 / (1 - np.exp(-w * self.w0))
            if np.abs(w_center - w) < 1.0e-8:
                break
        return w_center / (2 * np.pi * freq)

$\omega_{c}$の解析解はやっぱり難しいので、近似解を求めています。これがfor文のところですね。
$\omega_{c}$は$\omega_{0}$に近い値になるので、初期値を$\omega_{0}$としておくといいです。

ウェーブレットの計算

ウェーブレットの計算はほぼ数式通りです。

Morlet.py

    def _get_W(self, t):
        # calc wavelet
        k = np.exp(-0.5 * self.w0 ** 2)
        W = self.Cw / np.pi ** 0.25 *\
            np.exp(-0.5 * t ** 2) * (np.exp(1j * self.w0 * t) - k) # [n, s]
        return W

    def get_W(self, t, scale):
        # calc wavelet at scale s
        tt = t.reshape([1, -1]) / scale.reshape([-1, 1])
        W = self._get_W(tt) / scale.reshape([-1, 1]) ** 0.5
        return W

連続ウェーブレット変換と逆変換の実装

Morletクラスが少し長くなってしまいましたが、ようやく本番です。
連続ウェーブレット変換と逆変換を行うCWaveletクラスを実装していきましょう。
__init__メソッドはこんな感じ。

CWavelet.py

import numpy as np
from .Morlet import Morlet

class CWavelet(object):
    def __init__(self, fs, wavelet='morlet', w0=6.0, window_len=None,
        freq_range=None):

        self.fs = fs # sampling frequency
        self.dt = 1 / self.fs # sampling interval
        self.n_per_octave = 12
        self.window_len = window_len
        self.n = None
        self.W = None
        if wavelet == 'morlet':
            self.wavelet = Morlet(w0=w0) # Wavelet class
        else:
            raise ValueError('Unexpected wavelet: ' + str(wavelet))

        if freq_range is None:
            freq_range = (13.75, self.fs // 2)
        else:
            freq_range = (max(0, freq_range[0]), min(self.fs // 2, freq_range[1]))
        self.freq_period = self.get_freq_period(freq_range)
        self.scale = self.wavelet.freq2scale(self.freq_period)

対数スケールで等分された周波数の計算はget_freq_periodメソッドで取得しています。

CWavelet.py

    def _get_freq_log(self, freq_range):
        # get frequencies spaced at epual intervals on log2 scale.
        # frequencies on log2 scale are calculated from music keys based on 440Hz.
        k0 = int(self.n_per_octave * np.log2(freq_range[0] / 440)) # minimum key
        kn = int(self.n_per_octave * np.log2(freq_range[1] / 440)) # maximum key
        k = np.arange(k0, kn + 1, dtype=np.float64)
        freq_period = 440 * 2 ** (k / self.n_per_octave) # frequencies
        return freq_period

    def get_freq_period(self, freq_range):
        freq_period = self._get_freq_log(freq_range)
        return freq_period

連続ウェーブレット変換の実装

(4.1)(4.2)式に従って連続ウェーブレット変換を実装していくわけですが、式の通りに素直に実装してしまうと、スケールの数を$M$、時間長を$N$とした時に、計算量が$O(MN^2)$となってしまいます。
しかし、フーリエ変換を利用した畳み込みを行うことで、この計算量を$O(MN\log N)$に減らすことができます⁵。
フーリエ変換の畳み込み定理から以下の式が成り立ちます。

\int_{-\infty}^{\infty} f(\tau)g(t - \tau)\,d\tau = F^{-1}[\hat{f}(\omega)\hat{g}(\omega)] \tag{5.2.1}

ここで、$\hat{f}(\omega)$と$\hat{g}(\omega)$はそれぞれ$f(t)$と$g(t)$のフーリエ変換を表し、$F^{-1}[\cdot]$はフーリエ逆変換を表します。信号処理をやっているとお馴染みの式ですね。連続系で表しましたが、離散系でも成り立ちます。
(5.2.1)式を使うと(4.1)式は以下のように表せます。

\begin{align}
X_{l} &= \Delta t\sum_{n=-\infty}^{\infty} x[n]\,\overline{\psi}_{l, 0}[n - m]\\
&= \Delta t\sum_{n=-\infty}^{\infty} x[n]\,\overline{\psi'}_{l, 0}[m - n]\\
&= \Delta t \cdot F^{-1}[\hat{x}(\omega) \hat{\overline{\psi'}}_{a, 0}(\omega)] \tag{5.2.2}
\end{align}

ここで$\psi'[n]$は以下で表されます。

\psi'[n] = \psi[-n] \tag{5.2.3}

実際には高速フーリエ変換(FFT)を使うので、適切にパディングしてあげないと巡回畳み込みという別の計算になってしまうことに注意です。
また、ウェーブレット変換は$-\infty\leqq n\leqq \infty$の区間で和を取るのに対し、FFTは$0\leqq n\leqq N-1$の区間で和を取りますが、区間長$N$を十分大きくすれば、区間の両端におけるウェーブレットの値は限りなく0に近づくので、問題ありません。⁶

FFTで畳み込みを計算する部分を関数にするとこんな感じ。

fft_convolve

def fft_convolve(x1, x2):
    if x1.shape[-1] < x2.shape[-1]:
        x1, x2 = x2, x1
    x1_len = x1.shape[-1]
    x2_len = x2.shape[-1]
    s1 = np.fft.fft(x1, x1_len)
    s2 = np.fft.fft(x2, x1_len)
    y = np.fft.ifft(s1 * s2, x1_len)
    return y[..., x2_len - 1:]

この関数を使ってCWaveletクラスに連続ウェーブレット変換を計算するメソッドを実装します。

CWavelet.py

    def _transform_via_fft(self, x, strides=1):
        y = fft_convolve(x[..., np.newaxis, :], self.W[..., ::-1].conj())
        return y[..., ::strides]

    def _transform(self, x, strides=1):
        y = self._transform_via_fft(x, strides)
        #y = self._transform_directly(x, strides) # too late
        return y

    def _update_W(self, N):
        # if precomputed wavelet is not available, update wavelet.
        if self.window_len is None:
            window_len = 2 * N - 1
        else:
            window_len = self.window_len
        if self.W is None or self.n is None or window_len != self.n.shape[-1]:
            self.n = np.arange(-(window_len // 2), (window_len + 1) // 2)
            self.W = self.wavelet.get_W(self.n * self.dt, self.scale)

    def transform(self, x, strides=1):
        self._update_W(x.shape[-1])
        y = self.dt * self._transform(x, strides)
        return y

何度もウェーブレット変換を行う場合に毎回ウェーブレットを計算し直すのは無駄なので、_update_Wメソッドで再利用するか計算し直すか判断するようにしています。

逆変換の実装

逆変換の場合にもフーリエ変換による計算量削減が可能で、(4.2)式も(5.2.2)式と同じように変形できます⁷。

\begin{align}
x[n] &= \frac{2\ln 2 \cdot \Delta t}{C_{\psi}l_{0}}\sum_{l=-\infty}^{\infty} \frac{1}{a_{l}} \sum_{m=-\infty}^{\infty} X[l, m] \,\psi_{l, 0}[n - m]\\
&= \frac{2\ln 2 \cdot \Delta t}{C_{\psi}l_{0}}\sum_{l=-\infty}^{\infty} \frac{1}{a_{l}} F^{-1}[\hat{X_{l}}(\omega) \,\hat{\psi}_{l, 0}(\omega)] \tag{5.2.4}
\end{align}

逆変換もCWaveletクラスに実装するとこんな感じになります。

CWavelet.py

    def transform_inverse(self, y):
        self._update_W(y.shape[-1])
        xs = fft_convolve(y, self.W) / self.scale.reshape([-1, 1])
        coefficient = 2 * np.log(2) * self.dt / self.n_per_octave / self.wavelet.C
        x = coefficient * np.sum(xs.real, axis=-2)
        return x

使ってみる

実装したCWaveletクラスを使って実際に連続ウェーブレット変換を計算してみます。
今回はサンプリング周波数を44.1KHzとし、0.5~1.0秒で440Hz、1.5~2.0秒で880Hz、2.5~3.0秒で1760Hzのsin波を含む3.0秒の信号を解析します。
テストコードは以下。

test.py

import time
import numpy as np
import matplotlib.pyplot as plt
from wavelet.CWavelet import CWavelet

fs = 44100
f = 440
t = np.arange(fs // 2)
x = np.zeros(3 * fs, dtype=np.float64)
x[fs//2:fs] = np.sin(2 * np.pi * f * t / fs)
x[fs + fs // 2:2 * fs] = np.sin(2 * np.pi * 2 * f * t / fs)
x[2 * fs + fs // 2:3 * fs] = np.sin(2 * np.pi * 4 * f * t / fs)

wavelet = CWavelet(fs)
start = time.time()
y = wavelet.transform(x, strides=1)
end = time.time()
print(end - start)

fig = plt.figure()
ax = fig.add_subplot(111)
im = ax.imshow(np.abs(y) ** 2, aspect='auto', origin='lower')
ax.set_xticks(np.arange(0, y.shape[1], fs // 2))
ax.set_xticklabels(map(str, np.arange(0, 3, 0.5)))
ax.set_yticks(np.arange(0, y.shape[0], 12))
ax.set_yticklabels(map(str, wavelet.freq_period[::12]))
ax.set_xlabel('Time [s]')
ax.set_ylabel('Frequency [Hz]')
plt.colorbar(im)
fig.tight_layout()
plt.show()

start = time.time()
x2 = wavelet.transform_inverse(y)
end = time.time()
print(end - start)

fig = plt.figure()
ax = fig.add_subplot(211)
ax.plot(np.arange(x.shape[-1]) / fs, x)
ax.set_title('original')
ax = fig.add_subplot(212)
ax.plot(np.arange(x.shape[-1]) / fs, x2)
ax.set_title('recovered')
fig.tight_layout()

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x[fs // 2:fs // 2 + 500], label='original')
ax.plot(x2[fs // 2:fs // 2 + 500], label='recovered')
ax.legend(loc='upper right')
plt.show()

連続ウェーブレット変換によるスペクトログラムはこんな感じです。

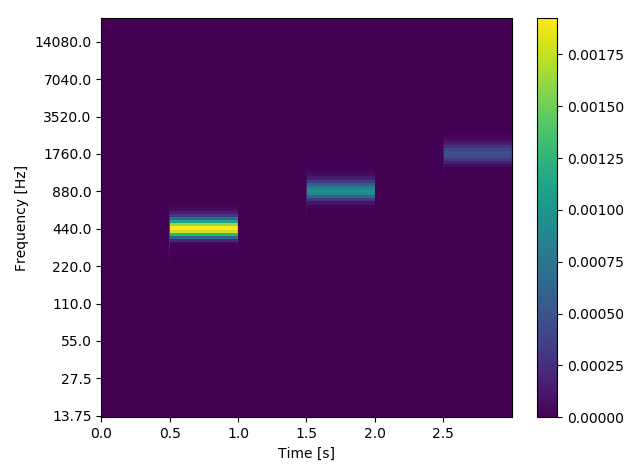
信号の振幅はどの周波数でも1ですが、スペクトログラムでは同じ値になっていませんね。ただし、これはバグではなく連続ウェーブレット変換の仕様のようです。
スペクトログラムの周波数毎のスケールを揃える方法は別記事に書こうと思います。（2019/08/31 書きました→続: 連続ウェーブレット変換を使ってみたかったので離散化して実装した）

逆変換の結果も見ておきましょう。

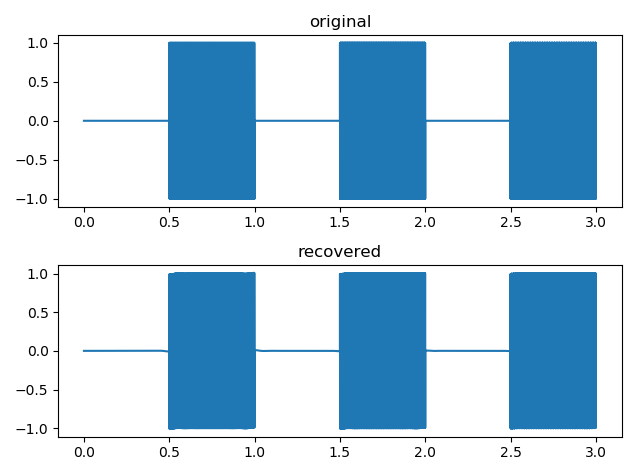
振幅が揃っているので(4.2)式の係数は合ってそう。0.5秒から500ポイント描画したものが以下です。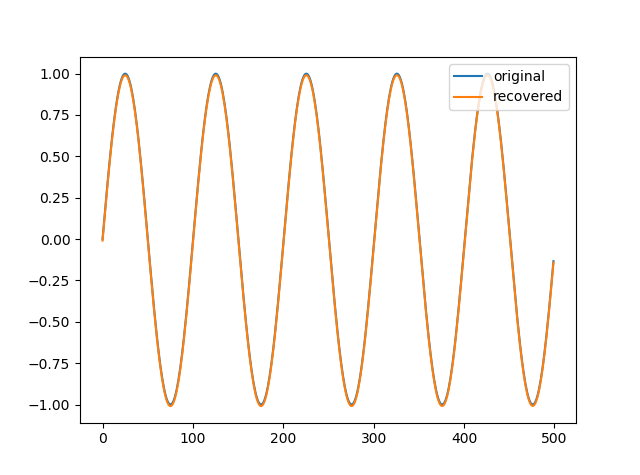
ピッタリ重なっていますね。大丈夫そうです。

まとめ

連続ウェーブレット変換を離散化した式を導出し、それをPython3で実装しました。
逆変換の近似の妥当性について詳しい検証が必要ですが、テストコードではうまく復元できていることが確認できました。

現在では、英語ができれば専門的な内容であってもネット上で情報を見つけることができます。しかし、そのようなページの中でも信憑性は微妙なページが少なからずあるという良い教訓になりました。
お盆休みを消し飛ばさないためにも、キチンとした文献を読んで学ぶことが大事ですね。

実装したコード全文はGitHubに上げています。

2019/08/31 離散化の問題点を考えた記事を書きました
続: 連続ウェーブレット変換を使ってみたかったので離散化して実装した

参考文献

I. Daubechies著, 山田道夫, 佐々木文夫訳, 「ウェーブレット10講」, 丸善出版, 2003年.
C. Torrence and G. P. Compo, "A Practical Guide to Wavelet Analysis", Bulletin of the American Meteorological Society, Vol.79, No.1, p.61-78, 1998.

今回の離散化は離散ウェーブレット変換と異なります。今回はあくまで連続ウェーブレット変換を使ってみようってことを目的としています。 ↩
英語版wikipediaのContinuous wavelet transformのページでは$2\pi$がありません。また、Matlab開発元のMathWorksの逆連続ウェーブレット変換のページでも$2\pi$がありません。 ↩
$a = \frac{\lambda}{l\Delta f}$とおけば、$\frac{da}{dl} = -\frac{\lambda}{l^{2} \Delta f} = -\frac{a}{l}$となるので、これを適用してあげれば導出できます。 ↩
$\frac{d}{d\omega}\hat{\psi}(\omega) = 0$とおいて計算していけば求められます。 ↩
厳密には$N$が2のべき乗の時に成り立ち、それ以外ではもう少し遅くなります。 ↩
重要な気がしたので追記しました。(2019/09/02) ↩
数式に間違いがあったため、一部削除・修正しました。(2019/08/21) ↩