続: 連続ウェーブレット変換を使ってみたかったので離散化して実装した

はじめに

以前「連続ウェーブレット変換を使ってみたかったので離散化して実装した」という記事を書きました。この記事の中ではタイトルの通り、連続ウェーブレット変換および逆変換を離散化した式を導出したのですが、逆変換は厳密には近似になっていて、その妥当性を検証していませんでした。
本記事では、その点を少し掘り下げて考えてみます。

なお、本記事では信号処理に関する知識がある程度必要となります。
信号処理については、ウェブ上だと「やる夫で学ぶディジタル信号処理」が詳しく、直感的でわかりやすいです。

環境

• python 3.7.3
• numpy 1.16.2
• scipy 1.2.1
• matplotlib 3.0.3

前記事のおさらい

連続ウェーブレット変換の離散化

実数の信号 $x(t)$ に対する連続ウェーブレット変換は以下のように表せます。

X(a, b) = \int_{-\infty}^{\infty} x(t) \, \overline{\psi}_{a,b}(t) \, dt \tag{1.1}

\psi_{a,b}(t) = \frac{1}{\sqrt{a}} \, \psi \Bigl(\frac{t - b}{a} \Bigr) \tag{1.2}

$\psi(t)$ はマザーウェーブレット、$a$はスケール、$b$は時間シフトで、$\overline{\psi}$ は $\psi$ の複素共役です。
一方で逆変換は以下のようになります。

x(t) = \frac{2}{C_{\psi}} \int_{0}^{\infty} \int_{-\infty}^{\infty} X(a, b) \, \psi_{a,b}(t) \, db \, \frac{da}{a^2} \tag{1.3}

この時、周波数$f$、スケール$a$、時間シフト$b$、時間$t$を(1.4)-(1.7)式のように離散化します。

f = f_{0} \cdot 2^{\frac{l}{l_{0}}} \tag{1.4}

a = \frac{\lambda}{f} = \frac{\lambda}{f_{0}} \cdot 2^{-\frac{l}{l_{0}}} \tag{1.5}

b = m\Delta t \tag{1.6}

t = n\Delta t \tag{1.7}

すると、連続ウェーブレット変換と逆変換はそれぞれ以下のように表せます。

X[l, m] = \Delta t \sum_{n=-\infty}^{\infty} x[n] \, \overline{\psi}_{l, m}[n] \tag{1.8}

x[n] = \frac{2\ln 2 \cdot \Delta t}{C_{\psi} l_{0}} \sum_{l=-\infty}^{\infty} \frac{1}{a_{l}} \sum_{m=-\infty}^{\infty} X[l, m] \, \psi_{l, m}[n] \tag{1.9}

ただし、$\psi_{l,m}[n]$ は以下で表されます。

\psi_{l, m}[n] = \frac{1}{\sqrt{a_{l}}} \, \psi \biggl( \frac{(n - m)\Delta t}{a_{l}} \biggr)

ここらへんの詳しい導出はこちら。

問題点

この離散化の問題点は2点あります。

問題点1. 周波数毎にウェーブレット変換のパワーが異なる

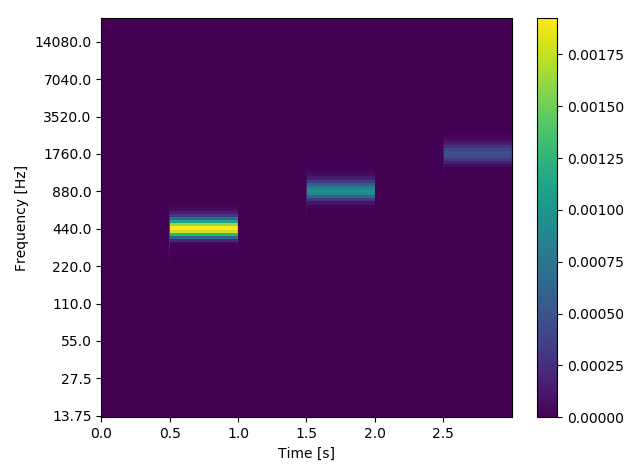
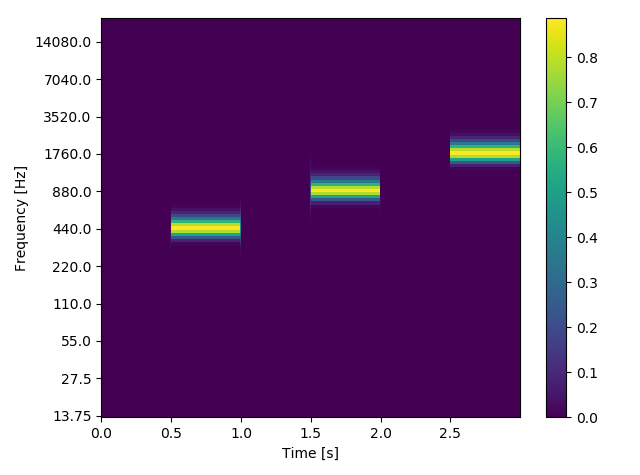
前記事でも載せていますが、振幅1.0で周波数を変化させた正弦信号に対するウェーブレット変換は以下のようになります。

__振幅は同じはずなのにウェーブレット変換後の値は異なっています。__これでは異なる周波数間でウェーブレット変換の結果を比べることができません。

問題点2. スケールの分解能の基準が不明

時間方向の離散化については、フーリエ変換から離散時間フーリエ変換の導出等、様々なところで用いられていて、自然かなと思います。
一方で__スケール方向の離散化については、どのくらい細かくすればよいか、基準となるものはなく__、時と場合によって考えなければなりません。
また、(1.9)式より、逆変換は各スケールの値を足し合わせるので、スケールの分解能が粗いと、復元した信号と元の信号の間に差が生まれてしまいます。一方でスケールの分解能が細かいとその分だけ計算量が増加し、時間がかかってしまいます。
そのため、スケールの分解能の選択は慎重に行わなければなりません。

システムとしての連続フーリエ変換（問題点1）

連続ウェーブレット変換は時間-周波数解析の手法ですが、別の方向から見ると、ある周波数特性を持った線形システムであると考えられます。
(1.1)(1.2)式から変形していくと以下の関係が得られます。

\begin{align}
X(a, b) &= \int_{-\infty}^{\infty} x(t) \, \overline{\psi}_{a,b}(t) \, dt\\
&= \int_{-\infty}^{\infty} x(t) \, \overline{\psi}_{a,0}(t-b) \, dt\\
&= \int_{-\infty}^{\infty} x(t) \, \overline{\psi'}_{a,0}(b-t) \, dt \tag{2.1}
\end{align}

ただし、$\psi'(t)$ は以下を満たします。

\psi'(t) = \psi(-t) \tag{2.2}

(2.1)式は$X(t)$ と $\overline{\psi'}(t)$ の畳み込み演算を表していて、$\overline{\psi'}(t)$ はシステムのインパルス応答と見ることができます。
フーリエ変換の畳み込み定理を用いると(2.1)式はさらに変形できます。

\begin{align}
X(a, b) &= \int_{-\infty}^{\infty} x(t) \, \overline{\psi'}_{a,0}(b-t) \, dt\\
&= F^{-1} \Bigl[ \hat{x}(\omega) \cdot \hat{\overline{\psi'}}_{a,0} \Bigr] \tag{2.3}
\end{align}

ここで、$F^{-1}[\cdot]$ はフーリエ逆変換を表します。(2.3)式から、ウェーブレット変換 $X(a,b)$ は時間信号 $x(t)$ に対し、各周波数成分を強めたり（振幅特性）、遅らせた（位相特性）ものであることがわかります。

Morletウェーブレットの場合

具体的にマザーウェーブレットとしてMorletウェーブレットを選んで、周波数特性を見てみましょう。Morletウェーブレットは以下の式で表されます。

\psi(t) = \frac{C_{\omega_{0}}}{\pi^{1/4}}e^{-\frac{1}{2}t^2}\,(e^{j\omega_{0}t} - e^{-\frac{1}{2}\omega_{0}^2}) \tag{2.4}

C_{\omega_{0}} = \Bigl(1 + e^{-\omega_{0}^2} - 2e^{-\frac{3}{4}\omega_{0}^2}\Bigr)^{-\frac{1}{2}} \tag{2.5}

ここで、Morletウェーブレットでは次式が成り立ちます。

\overline{\psi'}_{a,0}(t) = \overline{\psi}_{a,0}(-t) = \psi_{a,0}(t) \tag{2.6}

(2.1)式より、インパルス応答は $\overline{\psi'}(t)$ となりますが、(2.6)式より、これは $\psi_{a,0}(t)$ に等しくなります。

マザーウェーブレット $\psi(t)$ のフーリエ変換 $\hat{\psi}(\omega)$ は以下のように表せます。

\hat{\psi}(\omega) = \frac{C_{\omega_{0}}}{\pi^{1/4}} \Bigl( e^{-\frac{1}{2}(\omega - \omega_{0})^2} - e^{-\frac{1}{2}(\omega^2 + \omega_{0}^2)} \Bigr) \tag{2.7}

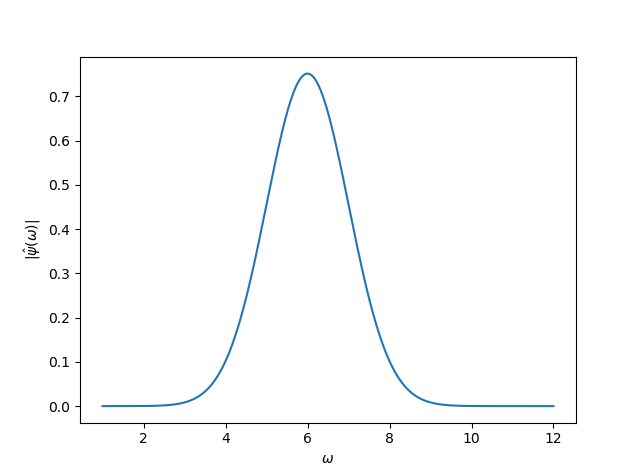
(2.7)式を見ると一目瞭然ですが、$\hat{\psi}(\omega)$ は実数なので、__Morletウェーブレットの位相特性は常にゼロ__です。振幅特性をプロットするとこんな感じ。

import numpy as np
import matplotlib.pyplot as plt

def get_c(w0):
    return (1 + np.exp(-w0 ** 2) - 2 * np.exp(-0.75 * w0 ** 2)) ** (-0.5)

def get_W_freq(w, w0):
    # return DTFT of Morlet wavelet
    c = get_c(w0)
    W = c / np.pi ** 0.25 *\
        (np.exp(-0.5 * (w0 - w) ** 2) - np.exp(-0.5 * (w0 ** 2 + w ** 2)))
    return W

w0 = 6
dw = 0.001
w = np.arange(1, w0 * 2, dw)
W_total = np.zeros(w.shape[-1], np.float64)
C = np.sum(get_W_freq(w, w0) ** 2 / np.abs(w)) * dw
W = get_W_freq(w, w0)

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(w, W)
ax.set_xlabel('$\omega$')
ax.set_ylabel('$|\hat{\psi}(\omega)|$')
plt.show()

振幅のピークを取る角周波数 $\omega_{c}$ は直接求めることは難しいのですが、以下の式を満たします。

\omega_{c} = \frac{\omega_{0}}{1 - e^{-\omega_{0}\omega_{c}}} \tag{2.8}

また、振幅のピークは $\omega = \omega_{c}$ として(2.8)式を(2.7)式に代入すればよいのですが、こちらも簡単な値にはなりません¹。

\hat{\psi}(\omega_{c}) = \frac{C_{\omega_{0}}}{\pi^{1/4}} \cdot \frac{\omega_{0}}{\omega_{c}} \cdot e^{-\frac{1}{2}(\omega_{c} - \omega_{0})^2} \tag{2.9}

$\omega_{c}$ はほぼ $\omega_{0}$ と同じ値になるので、以下の近似が成り立ちます。

\frac{\omega_{0}}{\omega_{c}} \approx 1 \tag{2.10}

e^{-\frac{1}{2}(\omega_{c} - \omega_{0})^2} \approx 1 \tag{2.11}

(2.10)(2.11)式より、(2.9)式は以下のように近似できます。

\hat{\psi}(\omega_{c}) \approx \frac{C_{\omega_{0}}}{\pi^{1/4}} \tag{2.12}

実際に計算してみると、$\omega_{0}=6.0$ の時、

\hat{\psi}(\omega_{c}) = 0.7511255444663539

\frac{C_{\omega_{0}}}{\pi^{1/4}} = 0.7511255444663542

となるので、実用の上ではこの差は無視できます。

スケールによる変化

ウェーブレット $\psi(\frac{t}{a})$ のフーリエ変換は $a,\hat{\psi}(a\omega)$ となるので、$\psi_{a,0}(t)$ のフーリエ変換 $\hat{\psi}_{a,0}(\omega)$ は以下のように表せます。

\begin{align}
\hat{\psi}_{a,0}(\omega) &= \frac{1}{\sqrt{a}} \cdot a \, \hat{\psi}(a\omega)\\
&= \sqrt{a} \, \hat{\psi}(a\omega) \tag{2.13}
\end{align}

(2.8)式の $\omega_{c}$ を用いると、$\hat{\psi}(\omega)$ のピークは $\omega_{c} = a\omega$ すなわち $\omega = \frac{\omega_{c}}{a}$ の時です。よって、(2.9)(2.11)式より、ピークの値 $\hat{\psi}(\frac{\omega_{c}}{a})$ は以下のように近似できます。

\begin{align}
\hat{\psi}_{a,0}\Bigl( \frac{\omega_{c}}{a} \Bigr) &= \sqrt{a} \cdot \hat{\psi}(\omega_{c})\\
&\approx \sqrt{a} \cdot \frac{C_{\omega_{0}}}{\pi^{1/4}} \tag{2.14}
\end{align}

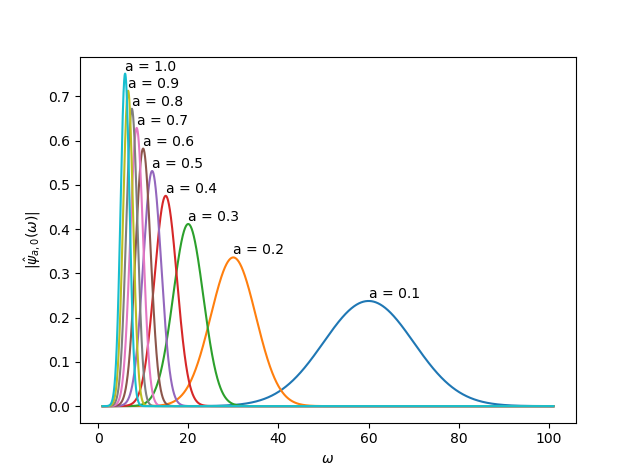
スケール$a$の値を変えていくつかプロットしたものが以下です。

w0 = 6
dw = 0.001
da = 0.1
w = np.arange(1, 101, dw)

fig = plt.figure()
ax = fig.add_subplot(111)
for i in range(10):
    a = (i + 1) * da
    Wi = get_W_freq(a * w, w0) * a ** 0.5

    ax.plot(w, Wi)
    x = w0 / a
    y = get_W_freq(w0, w0) * a ** 0.5
    ax.text(x, y, 'a = {:.1f}'.format(a), verticalalignment='bottom')
ax.set_xlabel('$\omega$')
ax.set_ylabel('$|\hat{\psi}_{a, 0}(\omega)|$')
plt.show()

__スケール$a$が減少するにつれて $\hat{\psi}(\omega)$ のピークが下がっています。_これが問題点1の原因です。
これは(2.14)式から明らかで、$\hat{\psi}(\omega)$ は $\sqrt{a}$ に比例しているからです。よって、$\psi{a, b}(t)$ に対して新たに $\frac{1}{\sqrt{a}}$ をかけてあげれば、(2.14)式における $\sqrt{a}$ が打ち消されて $\hat{\psi}_{a,0}(\omega)$ のピークがそろうはずです。

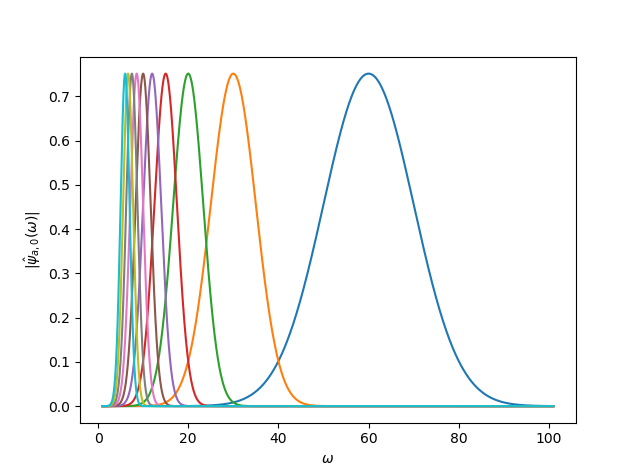
実際にプロットしてみると以下のようになります。

w0 = 6
dw = 0.001
da = 0.1
w = np.arange(1, 101, dw)

fig = plt.figure()
ax = fig.add_subplot(111)
for i in range(10):
    a = (i + 1) * da
    Wi = get_W_freq(a * w, w0)
    ax.plot(w, Wi)
ax.set_xlabel('$\omega$')
ax.set_ylabel('$|\hat{\psi}_{a, 0}(\omega)|$')
plt.show()

確かにスケールの値によらずピークがそろっています。
今回はMorletウェーブレットを例に具体的に計算しましたが、(2.13)式を見てわかる通り、基本的にはどのウェーブレットでも今回の補正が効くはずです。

問題点1の解決まとめ

ここまでの話から問題点1の解決をまとめると、離散化した連続ウェーブレット変換を以下のように修正してあげればよいことになります。

X(a, b) = \int_{-\infty}^{\infty} x(t) \, \overline{\psi}_{a,b}(t) \, dt \tag{1.1}

\psi_{a,b}(t) = \frac{1}{a} \, \psi \Bigl(\frac{t - b}{a} \Bigr) \tag{2.15}

また、この修正版に対する逆変換は以下のようになります。

x(t) = \frac{2}{C_{\psi}} \int_{0}^{\infty} \int_{-\infty}^{\infty} X(a, b) \, \psi_{a,b}(t) \, db \, \frac{da}{a} \tag{2.16}

元の式と比べると、$X(a, b)$ と $\psi_{a,b}(t)$ がそれぞれ $\frac{1}{\sqrt{a}}$ 倍されているので、逆変換では$a$倍して帳尻を合わせます。
離散化した場合でも同様に修正できて、ウェーブレット変換は以下のようになります。

X[l, m] = \Delta t \sum_{n=-\infty}^{\infty} x[n] \, \overline{\psi}_{l, m}[n] \tag{1.8}

\psi_{l, m}[n] = \frac{1}{a_{l}} \, \psi \biggl( \frac{(n - m)\Delta t}{a_{l}} \biggr) \tag{2.17}

また、逆変換も以下のようになります。

x[n] = \frac{2\ln 2 \cdot \Delta t}{C_{\psi} l_{0}} \sum_{l=-\infty}^{\infty}  \sum_{m=-\infty}^{\infty} X[l, m] \, \psi_{l, m}[n] \tag{2.18}

(1.8)(2.17)式を用いて問題点1の図を作成してみると、値がそろっているのがわかります。

システムとしての連続ウェーブレット逆変換（問題点2）

問題点2に関しても、線形システムの周波数特性を見る形で考えていきます。Morletウェーブレットの場合、(2.6)式より、(2.3)式は以下のように変形できます。

\begin{align}
X(a, b) &= F^{-1} \Bigl[ \hat{x}(\omega) \cdot \hat{\psi}_{a,0}(\omega) \Bigr] \tag{3.1}
\end{align}

同様にして、(2.16)式から連続ウェーブレット逆変換も以下のように表せます。

\begin{align}
x(t) &= \frac{2}{C_{\psi}} \int_{0}^{\infty} \int_{-\infty}^{\infty} X(a, b) \, \psi_{a,b}(t) \, db \, \frac{da}{a}\\
&= \frac{2}{C_{\psi}} \int_{0}^{\infty} \int_{-\infty}^{\infty} X(a, b) \, \psi_{a,0}(t-b) \, db \, \frac{da}{a}\\
&= \frac{2}{C_{\psi}} \int_{0}^{\infty} F^{-1} \Bigl[\hat{X}(a, \omega) \, \hat{\psi}_{a,0}(\omega) \Bigr] \, \frac{da}{a}\\
&= \frac{2}{C_{\psi}} \int_{0}^{\infty} F^{-1} \Bigl[\hat{x}(\omega) \, \hat{\overline{\psi'}}_{a,0}(\omega) \, \hat{\psi}_{a,0}(\omega) \Bigr] \, \frac{da}{a}\\
&= \frac{2}{C_{\psi}} F^{-1} \biggl[\hat{x}(\omega) \int_{0}^{\infty} \hat{\overline{\psi'}}_{a,0}(\omega) \, \hat{\psi}_{a,0}(\omega) \frac{da}{a} \biggr] \\
&= \frac{2}{C_{\psi}} F^{-1} \Bigl[\hat{x}(\omega) \, \hat{g}(\omega) \Bigr] \tag{3.2}
\end{align}

途中で $X(a,b)$ のフーリエ変換を $\hat{X}(a, \omega)$ と表しました。また、$\hat{g}(\omega)$ は $g(t)$ のフーリエ変換であり、$g(t)$ は以下で表されます。

g(t) = F^{-1} \biggl[\int_{0}^{\infty} \hat{\overline{\psi'}}_{a,0}(\omega) \, \hat{\psi}_{a,0}(\omega) \frac{da}{a} \biggr] \tag{3.3}

(3.2)式より、連続ウェーブレット変換と逆変換のセットは周波数特性が $\hat{g}(\omega)$ の線形システムと考えられます。
離散化した場合でも、フーリエ変換を離散時間フーリエ変換とすることにより、同様に示すことができます。

\begin{align}
x[n] &= \frac{2\ln 2 \cdot \Delta t}{C_{\psi} l_{0}} \sum_{l=-\infty}^{\infty} \sum_{m=-\infty}^{\infty} X[l, m] \, \psi_{l, m}[n] \\
&= \frac{2\ln 2 \cdot \Delta t}{C_{\psi} l_{0}} \sum_{l=-\infty}^{\infty} F^{-1}\Bigl[ \hat{X}(l, \omega) \, \hat{\psi}_{l, 0}(\omega) \Bigr] \\
&= \frac{2\ln 2 \cdot \Delta t}{C_{\psi} l_{0}} \sum_{l=-\infty}^{\infty} F^{-1}\Bigl[ \Delta t \, \hat{x}(\omega) \, \hat{\overline{\psi'}}_{l,0}(\omega) \, \hat{\psi}_{l,0}(\omega) \Bigr] \\
&= \frac{2\ln 2 \cdot (\Delta t)^2}{C_{\psi} l_{0}} F^{-1}\biggl[ \hat{x}(\omega) \, \sum_{l=-\infty}^{\infty} \hat{\overline{\psi'}}_{l,0}(\omega) \, \hat{\psi}_{l,0}(\omega) \biggr] \\
&= \frac{2\ln 2 \cdot (\Delta t)^2}{C_{\psi} l_{0}} F^{-1} \Bigl[ \hat{x}(\omega) \, \hat{g}(\omega) \Bigr] \tag{3.4}
\end{align}

$\hat{g}(\omega)$ は $g[n]$ の離散時間フーリエ変換であり、$g[n]$ は以下で表されます。

g[n] = F^{-1} \biggl[\; \sum_{l=-\infty}^{\infty} \hat{\overline{\psi'}}_{l,0}(\omega) \, \hat{\psi}_{l,0}(\omega) \biggr] \tag{3.5}

以上より、問題点2の焦点は、スケール$a$の離散化に対し、$\hat{g}(\omega)$ の振幅特性が周波数によらず一定であり、位相特性がゼロであるか、ということになります。

Morletウェーブレットの場合

先ほどと同じようにMorletウェーブレットを例に使ってみます。
Morletウェーブレットは(2.6)式の性質を持ちます。

\overline{\psi'}_{a,0}(t) = \overline{\psi}_{a,0}(-t) = \psi_{a,0}(t) \tag{2.6}

そのため、$\hat{g}(\omega)$ および ${g}(t)$ は以下のように変形できます。

\hat{g}(\omega) = \int_{0}^{\infty} \Bigl\{ \hat{\psi}_{a,0}(\omega)\Bigr\} ^2 \frac{da}{a} \tag{3.6}

g(t) = F^{-1} \biggl[ \; \int_{0}^{\infty} \Bigl\{ \hat{\psi}_{a,0}(\omega)\Bigr\} ^2 \frac{da}{a} \biggr] \tag{3.7}

離散化したものは以下の通り。

\hat{g}(\omega) = \sum_{l=-\infty}^{\infty} \Bigl\{ \hat{\psi}_{l,0}(\omega)\Bigr\} ^2 \tag{3.6}

g[n] = F^{-1} \biggl[ \; \sum_{l=-\infty}^{\infty} \Bigl\{ \hat{\psi}_{l,0}(\omega)\Bigr\} ^2 \biggr] \tag{3.7}

離散化した時のスケール$a$とインデックス $l$ の関係は以下のように設定していました。

f = f_{0} \cdot 2^{\frac{l}{l_{0}}} \tag{1.4}

a = \frac{\lambda}{f} = \frac{\lambda}{f_{0}} \cdot 2^{-\frac{l}{l_{0}}} \tag{1.5}

$l_{0}$ はスケール$a$を離散化した時の「細かさ」にあたる部分で、このパラメータを変えることで $\hat{g}(\omega)$ が大きく変化してしまいます。
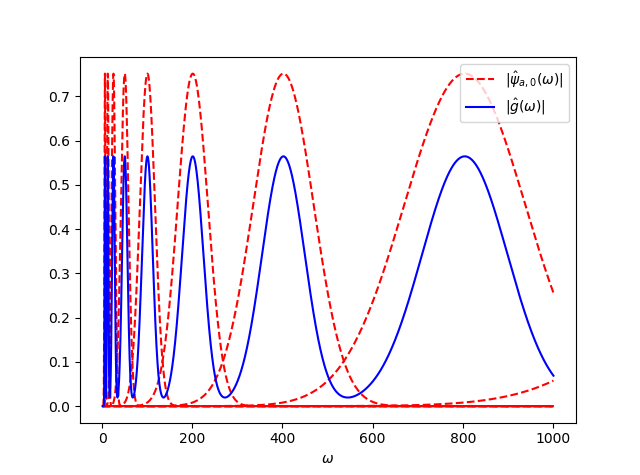
具体的に振幅特性をプロットしてみましょう。$l_{0}=1$の場合が以下です。

w0 = 6
dw = 0.01
l0 = 1
w = np.arange(1, 1001, dw)
W_total = np.zeros(w.shape[-1], np.float64)

fig = plt.figure()
ax = fig.add_subplot(111)

for i in range(120):
    a = w0 / (2 * np.pi * 2 ** (i / l0))
    Wi = get_W_freq(a * w, w0)
    W_total += Wi ** 2

    if i == 0:
        ax.plot(w, Wi, 'r--', label='$|\hat{\psi}_{a, 0}(\omega)|$')
    else:
        ax.plot(w, Wi, 'r--')

ax.plot(w, W_total, 'b-', label='$|\hat{g}(\omega)|$')

ax.set_xlabel('$\omega$')
ax.legend(loc='upper right')
plt.show()

青線が $\hat{g}(\omega)$ で、赤点線が $\hat{\phi}(\omega)$ です。(3.4)式から、$\hat{g}(\omega)$ の振幅特性は周波数によらず一定であってほしいのですが、$l_{0}=1$ の時は大きく上下してしまっています。これでは元の信号を正しく復元できません。
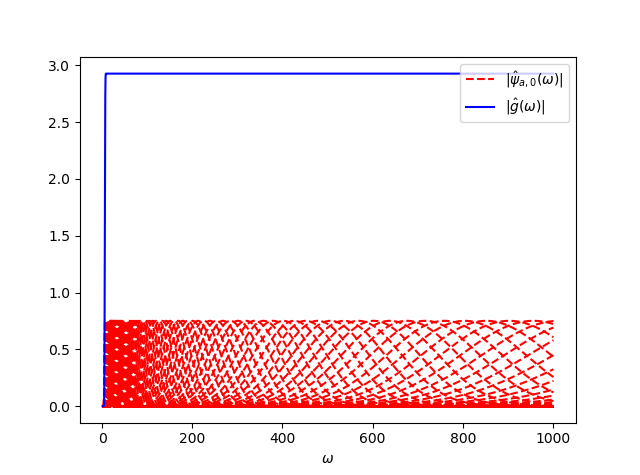
$l_{0}=12$ の時はどうでしょうか。（コードは3行目を12に変えただけなので省略）

どの周波数でも同じ値になっていて、なんかすごく良さそうです。一番小さいスケールに対応する周波数は $2^{0}(=1.0)$ Hzで、この付近より小さい周波数成分はカットされてしまいますが、それより高い周波数成分はうまく復元できそうです。
scipy.signalのargrelmax関数を使ってピークのインデックスを検出し、周波数が一番小さいピークの周波数を計算してみます。

from scipy.signal import argrelmax

indices = argrelmax(W_total)[0] # [1047, 1052, 1056, ...]
print('minimum freq of peak: {:}'.format(w[indices[0]] / (2 * np.pi)))
print('value: {:}'.format(W_total[indices[0]]))

minimum freq of peak: 1.825507197264041
value: 2.927263635035609

結果は約1.8Hzでした。これよりも小さい周波数成分はうまく復元できなさそうです。今回は $l$ を0~120として和を取ったのでこのような結果になりましたが、この範囲を負の値にも広げれば1.8Hz未満の周波数成分もうまく復元できるようになるはず²です。

一方で、図の中では平坦と思われる部分も実際には変化している可能性があります。それを検証してみましょう。
具体的には、1.8Hz以上の周波数における最大値と最小値を比較します。

print('min: {:}'.format(np.amin(W_total[indices[0]:])))
print('max: {:}'.format(np.amax(W_total[indices[0]:])))

min: 2.9272636350254504
max: 2.9272636350356254

$10^{-11}$ くらいの差しかありませんね。デシベル単位だと約-110dBです。この差を許容するかどうかは使う場面によって変わりますが、十分使える余地はあるかなーという印象です³。
また、位相特性については、Morletウェーブレットではどの周波数でもゼロなので、考慮しなくてよいのは嬉しいところですね。

問題2の解決まとめ

以上から、スケールの分解能の基準は、ウェーブレット変換と逆変換をセットで考えた場合の周波数特性を見ることで判断できることが分かりました。

\hat{g}(\omega) = \sum_{l=-\infty}^{\infty} \hat{\overline{\psi'}}_{l,0}(\omega) \, \hat{\psi}_{l,0}(\omega) \tag{3.8}

実際の検証から、Morletウェーブレットでは、$l_{0}=12$ 程度（12平均律）であれば離散化の影響はほとんどないといえるのではないでしょうか。

まとめ

以上で前記事で残した問題点の検証は終わりです。離散化した連続ウェーブレット変換と逆変換では、以下のverを使うと振幅がそろいます。

\psi_{l, m}[n] = \frac{1}{a_{l}} \, \psi \biggl( \frac{(n - m)\Delta t}{a_{l}} \biggr) \tag{2.17}

X[l, m] = \Delta t \sum_{n=-\infty}^{\infty} x[n] \, \overline{\psi}_{l, m}[n] \tag{1.8}

x[n] = \frac{2\ln 2 \cdot \Delta t}{C_{\psi} l_{0}} \sum_{l=-\infty}^{\infty}  \sum_{m=-\infty}^{\infty} X[l, m] \, \psi_{l, m}[n] \tag{2.18}

また、スケール$a$の分解能は以下で表される $\hat{g}(\omega)$ の周波数特性を見て判断しましょう。

\hat{g}(\omega) = \sum_{l=-\infty}^{\infty} \hat{\overline{\psi'}}_{l,0}(\omega) \, \hat{\psi}_{l,0}(\omega) \tag{3.8}

前記事と合わせて軽く書くつもりでしたが、なんだかすごい量になってしまいました…
信号処理については勉強しているつもりですが、何か間違い、不明瞭な点があったらコメントで指摘していただけると嬉しいです。

1. 自分の数学力ではこれくらいが限界でしたが、もっときれいな形があれば教えてください。 ↩

2. 周波数を2のべき乗で取る場合、指数をいくら小さくしても周波数は0にはなりません。そのため、本来であれば、元の信号の直流成分を計算しておいて逆変換後に足すことが必要です。 ↩

3. $l_{0}=12$で不十分な場合は24や48として細かくしていけばよいです。 ↩