はじめに
以前、Web メルカトル(EPSG:3857)について整理するという記事で、以下のような記載をしました。
WGS84で得られた経緯度を、真球(半径は、WGS84準拠楕円体の長半径に相当)を仮定してメルカトル投影を行っています。
楕円体で得られた経緯度を、楕円体ではなく真球を仮定して投影しているため、実は、厳密には正角図法ではありません。
この際、真球を仮定して投影するか、回転楕円体として投影するかでどのように差が出るのか気になります。
なお、epsg.io の EPSG:3857の説明には、以下のような記載があります。
Relative to WGS 84 / World Mercator (CRS code 3395) gives errors of 0.7 percent in scale and differences in northing of up to 43km in the map (21km on the ground).
ここには、回転楕円体のメルカトル投影である EPSG:3395と比較して、0.7%の誤差が生じると記載されています。図上(メルカトル図法の座標値のことだと思います)で43 km、地上距離として21 kmのずれに相当するようです。
今回は、EPSG:3857(Web メルカトル)と EPSG:3395(World メルカトル)の誤差を日本周辺で見ていきたいと思います。
日本周辺での誤差
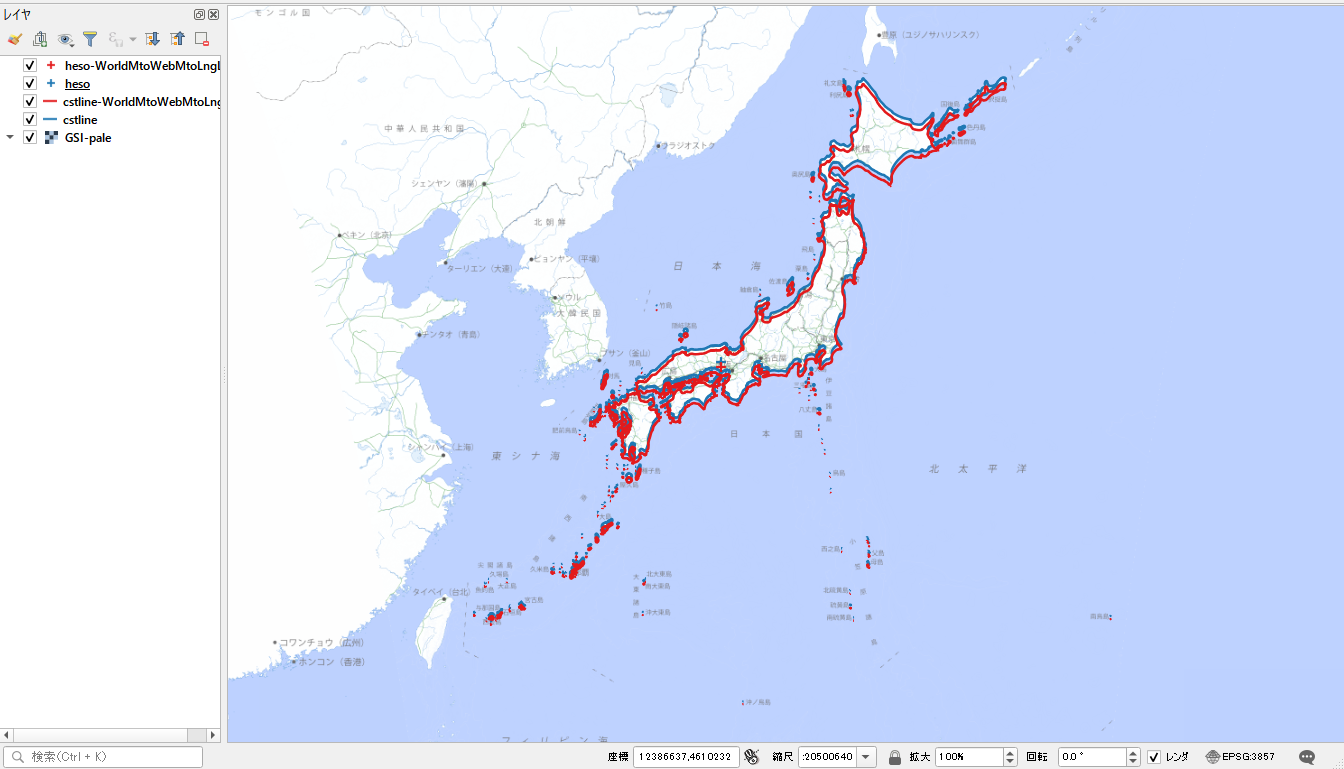
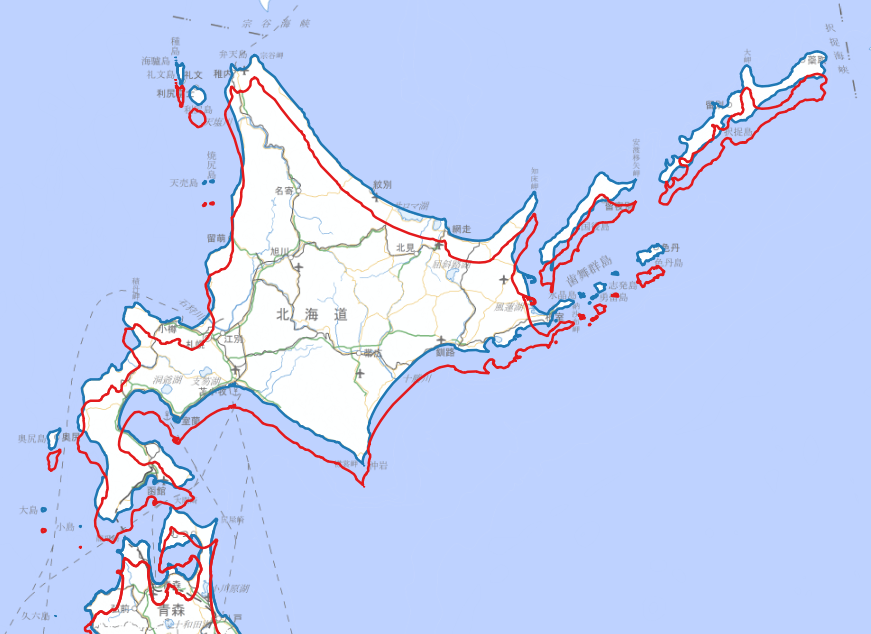
まずは、地理院地図Vector から取得した日本の海岸線のデータを使って比較してみます。
以下の図で、青色が Web メルカトルで投影した海岸線です。背景の地理院タイル(淡色地図)も Web メルカトルで投影しています。
そして、赤色の海岸線が、元データの経緯度を World メルカトルへ変換して得られた座標値を Web メルカトルとして表示したものです。
Web メルカトルは World メルカトルと比較して、北方向へ間延びして表示されることが分かります。
兵庫県の十字マークは、(東経135度、北緯35)の点です。この点の座標値を見てみます。
| Web メルカトル | World メルカトル |
|---|---|
| (15028131.3, 4163881.1) | (15028131.3, 4139372.8) |
経度方向(X 座標)は同じですが、緯度方向(Y 座標)で、メルカトル図法の座標値(図上距離)として24,508 m(24.5 km)の違いが生じていることが分かります。約0.5%相当です。
ただし、これは赤道からの累積の差です。特定の範囲内での差を考えると差はもう少し小さくなりそうですので、たとえば、(東経135度、北緯35の点)と(東経135度、北緯35.1度)の点の距離を調べてみましたが、それでも、約0.45%の誤差が生じることが分かります。
| 北緯 | Web メルカトル | World メルカトル |
|---|---|---|
| 35.1度 | 4177479.1 | 4152909.5 |
| 35度 | 4163881.1 | 4139372.8 |
| 図上距離 | 13598.0 | 13536.8 |
タイル単位で比較する
Web メルカトルはウェブ地図で利用されることが多いですから、ウェブ地図で組み合わせて利用されるタイル(Slippy map tilenames 形式)単位での誤差も把握しておきましょう。
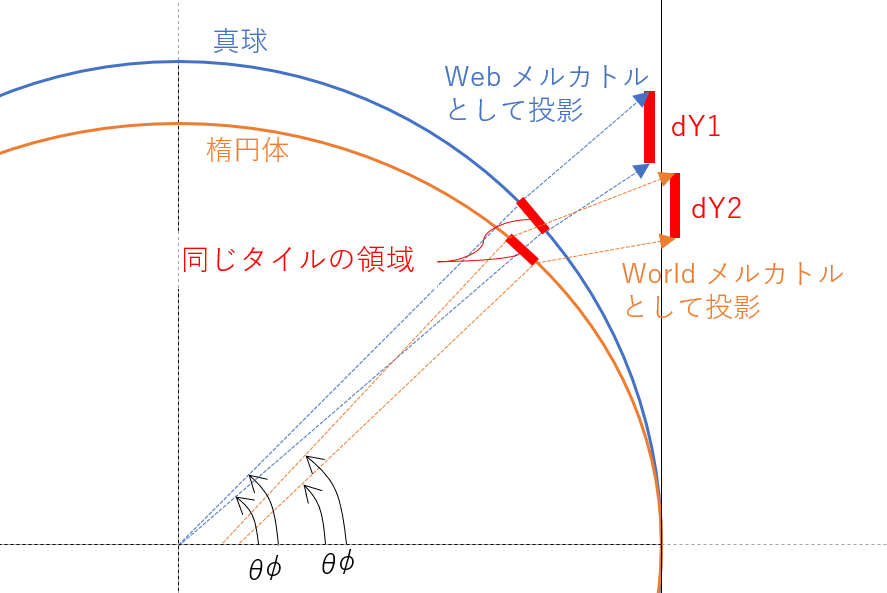
以下の表は東京駅周辺を含むタイルについて、ズームレベル(ZL)を変更させてタイルの1辺の長さ(Y 座標方向)を調べてみました。比較の概要(模式図)は以下の通りです。
誤差は、ZL が小さいうちはタイルの範囲が大幅に変わる関係で振動していますが、ZL が大きくなるとおおよそ0.44%間延びすることとなります。
| タイル座標 | dY1(Web メルカトル) | dY2(World メルカトル) | 誤差 |
|---|---|---|---|
| 2/3/1 | 10018754 | 9979520 | 0.39% |
| 3/7/3 | 5009377 | 4981349 | 0.56% |
| 4/14/6 | 2504689 | 2492621 | 0.48% |
| 5/28/12 | 1252344 | 1246927 | 0.43% |
| 6/56/25 | 626172 | 623306 | 0.46% |
| 7/113/50 | 313086 | 311692 | 0.45% |
| 8/227/100 | 156543 | 155856 | 0.44% |
| 9/454/201 | 78272 | 77926 | 0.44% |
| 10/909/403 | 39136 | 38962 | 0.45% |
| 11/1819/806 | 19568 | 19481 | 0.44% |
| 12/3638/1612 | 9784 | 9741 | 0.44% |
| 13/7276/3225 | 4892 | 4870 | 0.44% |
| 14/14552/6451 | 2446 | 2435 | 0.44% |
| 15/29105/12903 | 1223 | 1218 | 0.44% |
| 16/58211/25806 | 611 | 609 | 0.44% |
| 17/116423/51613 | 306 | 304 | 0.44% |
| 18/232846/103226 | 153 | 152 | 0.44% |
※誤差は、Web メルカトル上での長さ(dY1)と World メルカトル上での長さの差(dY2)を、World メルカトル上での長さ(dY2)で割ったものです。
※World メルカトルの適用範囲は南緯80度~北緯84度で、Web メルカトルの北端を含まないので、ZL0~1は除外しています。
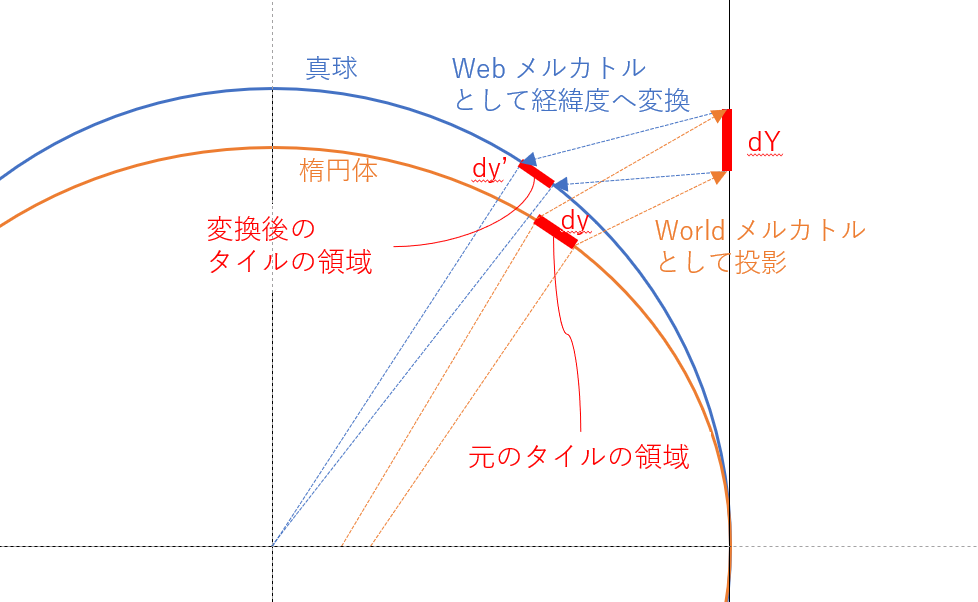
また、地上での各タイルの北端・南端の緯度について、World メルカトルへ変換したのち、World メルカトルの座標値を Web メルカトルのものとして経緯度に戻し、回転楕円体上の距離を測定しました。この変換の概要(模式図)は以下の通りです。測定には、地理院地図の距離測定機能のコードを利用しました。
誤差は、ZL が大きくなるとおおよそ0.22%となることが分かります。
| タイル座標 | 緯度差 | 緯度差(変換後) | dy | dy'(変換後) | 誤差 |
|---|---|---|---|---|---|
| 18/232846/103226 | 0.0011 | 0.0011 | 124 m | 123 m | 0.22% |
| 17/116423/51613 | 0.0022 | 0.0022 | 248 m | 247 m | 0.22% |
| 16/58211/25806 | 0.0045 | 0.0045 | 495 m | 494 m | 0.22% |
| 15/29105/12903 | 0.0089 | 0.0089 | 990 m | 988 m | 0.22% |
| 14/14552/6451 | 0.0178 | 0.0178 | 1980 m | 1976 m | 0.22% |
| 13/7276/3225 | 0.0357 | 0.0356 | 3960 m | 3951 m | 0.22% |
| 12/3638/1612 | 0.0714 | 0.0712 | 7918 m | 7901 m | 0.22% |
| 11/1819/806 | 0.1428 | 0.1425 | 15843 m | 15809 m | 0.22% |
| 10/909/403 | 0.2858 | 0.2852 | 31715 m | 31645 m | 0.22% |
| 9/454/201 | 0.5707 | 0.5694 | 63317 m | 63180 m | 0.22% |
| 8/227/100 | 1.1372 | 1.1349 | 126185 m | 125919 m | 0.21% |
| 7/113/50 | 2.2907 | 2.2857 | 254156 m | 253586 m | 0.22% |
| 6/56/25 | 4.6457 | 4.6343 | 515339 m | 514054 m | 0.25% |
| 5/28/12 | 9.0277 | 9.0099 | 1001793 m | 999782 m | 0.2% |
| 4/14/6 | 19.0369 | 18.9796 | 2110847 m | 2104441 m | 0.3% |
| 3/7/3 | 40.9799 | 40.7895 | 4538341 m | 4517202 m | 0.47% |
| 2/3/1 | 66.5133 | 66.3724 | 7380073 m | 7364366 m | 0.21% |
※誤差は、もともとのタイルの辺長(dy)と 変換後の辺長(dy')の差を、変換後の辺長で割ったものです。
図上での許容誤差
兵庫~東京近辺のみを表示する場合、図上の誤差はおおよそ0.45%くらいであることが分かりました。この誤差を、たとえば 0.1 mm 以内に収めたいという場合、南北で 22 cm のサイズまでなら、Web メルカトルと World メルカトルの違いを気にしなくても良さそうです。
(ただし、もともとメルカトル図法では、緯度に応じて距離が異なるため、厳密に図面内での誤差を一定値以下に収めるには追加の検討が必要です。)
参考
こちらの方も、Web メルカトルの性質等についてまとめておられます。
おわりに
今回、Web メルカトルと World メルカトル の違いを確認しました。世界地図に重ねるとかなり大きい違いが生じることが分かりましたが、とはいえ、小数点以下数%の伸び縮みをどこまで影響するかといえば、ウェブ地図を閲覧する上では特に気にすることもないでしょう。私自身、世界地図を出されて Web メルカトルか World メルカトルかを目視で気づけるとは思えません。
ずれは大きいですので、適切な投影法を選択していなければ、地図データの重ね合わせの際、特に大縮尺で大変なことになりますが、それはどの投影法にも言えることです。
距離を測るときに問題となりそうですが、今となっては、紙に打ち出して定規を当てるよりも、ウェブ地図の機能で測定することの方が一般的かと思います。(たとえば、地理院地図は、Web メルカトルの座標値ではなく、独立した手法で元の経緯度から距離を計算しています。)
紙の地図とは異なり、ウェブ地図の世界では、表示の話と、各種 GIS 的な処理の話は分離して処理することができます。そう考えると、表示のためと割り切って、回転楕円体で得られた経緯度を真球と仮定して表示するという考え方は結構合理的かなと思います。