はじめに
Web 地図でよく利用されているタイル形式(Slippy map tilenames 形式)ですが、多くの場合、Pseudo-Mercator や Web メルカトルと呼ばれる投影法で表示されています。EPSG には3857で登録されています。この投影法について、あまりしっくりくる説明が見つからなかったので、色々調べて自分なりに理解した結果を記事に残してみます。
なお、地理院タイルの地図投影法の説明では、以下のような説明があります。
世界測地系※の経緯度が正方形に変換されるよう極域の一部地域(北緯及び南緯約85.0511度以上)を除外した範囲について、メルカトル投影の数式を使って変換します。
※ 地理院タイルの測地系は、日本国内の地図については、世界測地系(JGD2011)です。
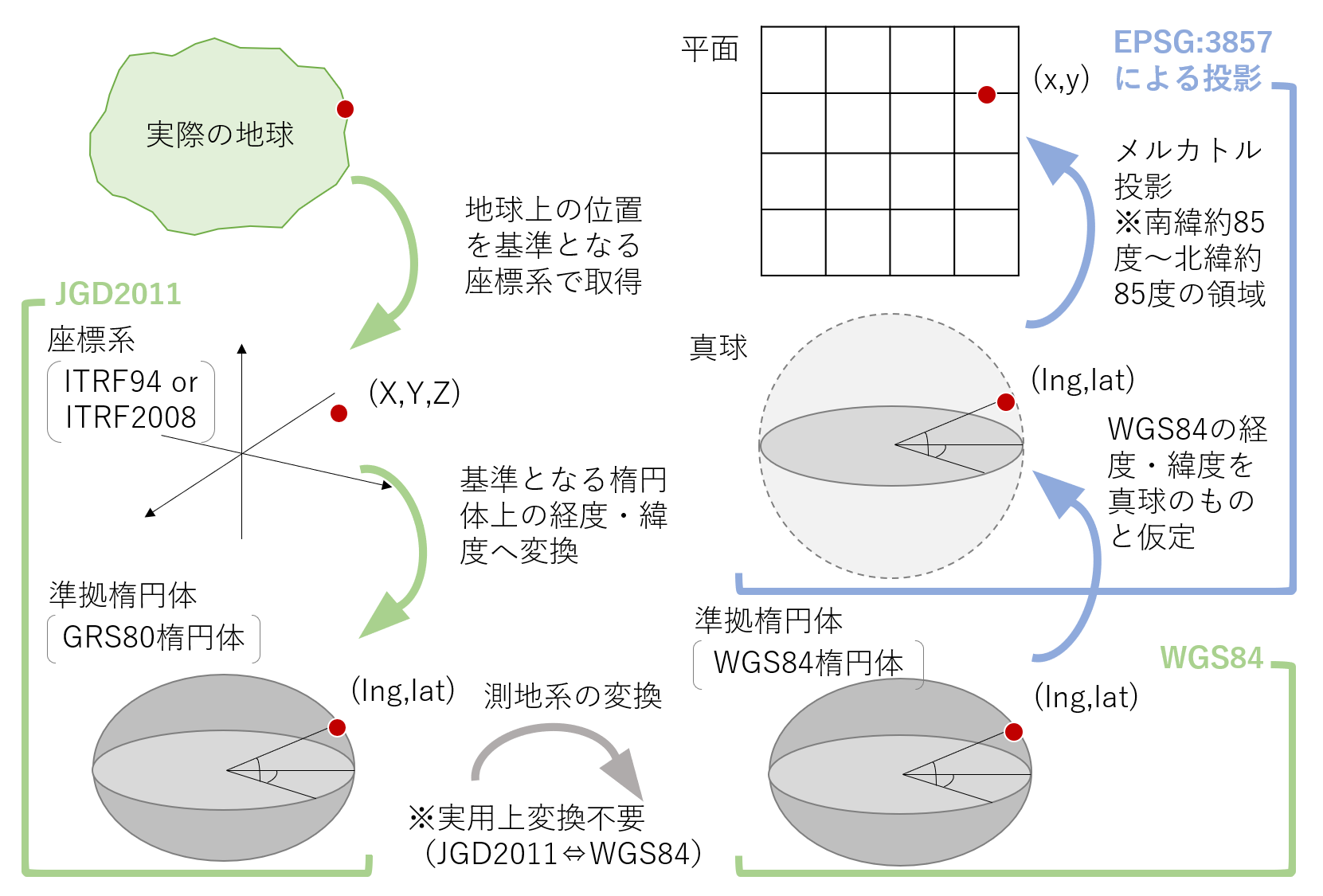
ここで、JGD2011との関係も理解するために、測地系から考えてみたいと思います。
測地系と地図投影法
国土地理院によると、測地系とは、地球上で位置を測る際のルールとそれに従って定められた座標です。たとえば、地球上の位置を地球を模した楕円体上に経度・緯度(と標高)に表現するのが測地系の範囲でしょう。一方、球体上の点(経度・緯度)を2次元の紙面上(Web 画面上も含む)の座標へと表現するのが地図投影法と理解しています。
日本の基本測量・公共測量では「世界測地系」と呼ばれる世界で共通に利用できる測地系が採用されています(測量法第11条等に基準が記載されています)。現在、日本が採用している測地系は、「日本測地系2011」(JGD2011) です。
ある点を経度・緯度に表現するには、座標系と準拠楕円体が必要となります。座標系で位置と方向の基準を定め、準拠楕円体はその座標値を経緯度へ変換するのに必要となります。なお、測量法上、地理学的経緯度を使うこととなっています。
JGD2011の前の JGD2000では、ITRF94座標系と GRS80の楕円体を使用して経度・緯度を示していました。一方、東日本大震災後、影響の大きい地域で成果の改定を行っており、その際、改定のあった地域は、座標系を ITRF2008 座標系に改められています。そのため、JGD2011では、地域によって基準座標系が ITRF94座標系と ITRF2008座標系と異なります。ただし、その違いによる乖離は調整計算により解消されているようです。準拠楕円体は GRS80楕円体から変更ありません。
その他の測地系としてよく聞くものに、WGS84があります。米国が構築・維持しており、GPS でも使われている世界測地系です。WGS84は、現在では ITRF 系とほとんど同一のものといえ、両者で変換の必要はないとのことです。
以下、上記記述の引用元・参考資料となります。
メルカトル図法
メルカトル図法は、正角図法であり、地球上の角度と紙面上の角度が等しくなるように表現した図法です。角度が保存されるため、局所的な形状は正確なものとなります(参考:国際興業)。
メルカトル図法では、紙面上で経線は平行に表されます。一方、緯度が大きくなるほど、実際の経線同士の距離は狭くなることから、紙面上では緯度が大きくなるほど、経度の差が拡大して表示されることになります。角度を正しく表示するためには、緯線の間隔を、経度の差に合わせて拡大して表示する必要があります。
なお、基準となる円弧を赤道ではなく、任意の子午線とした横メルカトル法もあり、地形図でも利用されるユニバーサル横メルカトル法や平面直角座標系はその一種(ガウス・クリューゲル投影法)です。
EPSG:3857について
本題の EPSG:3857です。EPSG には "Pseudo-Mercator" として登録されていますが、Web メルカトル等とも呼ばれています。なかなか良い説明がなく、探した中では、Wikipedeia の解説が充実してわかりやすいと思われます。
手順としては、WGS84で得られた経緯度を、真球(半径は、WGS84準拠楕円体の長半径に相当)を仮定してメルカトル投影を行っています。(PROJ4 では、+proj=merc +a=6378137 +b=6378137 ... と表現されています。)楕円体で得られた経緯度を、楕円体ではなく真球を仮定して投影しているため、実は、厳密には正角図法ではありません。
メルカトル投影をすると、極に近くなるほど、緯度方向が引き延ばされることになります。そのため、緯度がおおよそ85度以上の地域を表示しないこととし、南緯約85度~北緯約85度の領域をちょうど正方形で表示しています。
参考ですが、EPSG:3857で投影されたデータを Slippy map tilenames 形式でタイル化すると、ズームレベルが大きくなるにつれて、タイル1枚当たりの X 方向、Y 方向の長さの差が小さくなり、実際の正方形へ近づきます。上述の通り、厳密には正角図法ではありませんが、局所的にはおおよそ形状が正しいものに近づくと分かります。以下は東京駅周辺のタイルについて、ズームレベルを上げていき、X 方向、Y 方向の長さがどのように変化するか調べた例です。
| ズームレベル | 差の比率 | 辺長(X 方向) | 辺長(Y 方向) | タイル座標 |
|---|---|---|---|---|
| 18 | 0.45% | 124 m | 124 m | 18/232846/103226 |
| 17 | 0.45% | 249 m | 248 m | 17/116423/51613 |
| 16 | 0.45% | 497 m | 495 m | 16/58211/25806 |
| 15 | 0.45% | 995 m | 990 m | 15/29105/12903 |
| 14 | 0.46% | 1989 m | 1980 m | 14/14552/6451 |
| 13 | 0.47% | 3978 m | 3960 m | 13/7276/3225 |
| 12 | 0.49% | 7957 m | 7918 m | 12/3638/1612 |
| 11 | 0.53% | 15928 m | 15843 m | 11/1819/806 |
| 10 | 0.62% | 31913 m | 31715 m | 10/909/403 |
| 9 | 0.8% | 63825 m | 63317 m | 9/454/201 |
| 8 | 1.16% | 127649 m | 126185 m | 8/227/100 |
| 7 | 1.86% | 258885 m | 254156 m | 7/113/50 |
| 6 | 3.18% | 531740 m | 515339 m | 6/56/25 |
| 5 | 6.12% | 1063120 m | 1001793 m | 5/28/12 |
| 4 | 10.01% | 2322212 m | 2110847 m | 4/14/6 |
| 3 | 10.38% | 5009377 m | 4538341 m | 3/7/3 |
| 2 | 35.75% | 10018754 m | 7380073 m | 2/3/1 |
| 1 | 111.7% | 20003931 m | 9449220 m | 1/1/0 |
※距離の計算には、地理院地図で利用されている計算方法を利用。X 方向は南側の辺で算出。差の比率は (X-Y)/Y の百分率。
まとめ
以上のことをまとめると、以下のような手順で位置の取得~投影までなされるものと整理できそうです。
最後に、メルカトル投影された平面を Slippy map tilenames の形式に分割すれば、タイルが完成です。