Glow: Better Reversible Generative Modelsメモ

Glow: Generative Flow with Invertible 1x1 Convolutionsを読んだ際のメモ（途中から適当な訳を入れただけになっている）

まとめ

NICE、RealNVPを改善したフローベースの生成モデルの提案。1x1の畳み込み層を導入することで改善。
提案モデルの利点

• 対数尤度や潜在変数を直接求める事が可能
  • 画像変換（補完など）などの関連タスクがやりやすい
• 高解像画像を生成可能

• 並列化が可能

• 評価

  • 評価は、RealNVPと生成画像の対数尤度を比較して、いい結果を得た
  • 定性評価は、サンプリングや2画像間の補完などをCeleb-A HQで実施

参考ページ

• デモページ Glow: Better Reversible Generative Models
• github リポジトリ
• 論文 Glow: Generative Flow with Invertible 1x1 Convolutions
• 提案のもととなる研究
  • NICE
  • RealNVP

Abstruct

• 提案手法Glowは、1 x 1 の可逆な畳込み層を用いたシンプルなフローベース生成モデル
• フローベースの生成モデルは学習時、生成時ともに以下の点で魅力的
  • 対数尤度と潜在変数を直接求められる
  • 並列化が可能
• 提案手法を用いることで、ベンチマークより生成画像の対数尤度は著しく改善した
• 対数尤度ベースモデルでは難しかった以下を可能にした
  • 高解像画像（サイズの大きな画像）の生成
  • 高解像画像の自然な操作・変更

Introduction

生成モデルの整理

• 敵対的生成ネットワーク（GAN）
• 対数尤度ベース手法
  1. 自己回帰型（Autoregressive）
     • PixelCNNなど
     • シンプルさが利点
     • 生成が並列化できず、大きなサイズの画像生成や動画では問題
  2. 変分自己符号化（Variationl AutoEncoder）
     • VAE
     • 対数尤度の下界最適化
     • 並列化可能だが、最適化自体が難しい
  3. フローベースモデル
     • NICEで提案され、RealNVPで拡張
     • 提案のGlowはこのクラス

参考

• 論文紹介 Pixel Recurrent Neural Networks

フローベースモデルとは

GANやVAEに比べて注目されてないが、フローベースの生成モデルは以下の利点がある

• 直接的な潜在変数の推定と対数尤度の評価
  • VAEはデータに対応する潜在変数を近似的に推定
  • GANでは潜在変数を推定するためのエンコーダがそもそも存在しない
  • リバーシブルな生成モデルでは、近似なしに直接推定が可能。これにより推定が正確になるだけでなく、対数尤度を下界を使わず直接最適化することができる
• 効率的な推定と生成
  • PixelCNNのようなAutoregressiveModelはリバーシブルだが、並列化に向いてなく、効率的に計算できない
  • GlowやRealNVPのようなフローベースの生成モデルでは、推定・推定の両者で並列が可能
• 付随タスクでの潜在空間の使い勝手の良さ
  • AutoregressiveModelは隠れ層の周辺分布が分からないため、うまく生成画像操作するのが難しい
  • GANでは、エンコードが無いことで、データを直接に潜在空間で表現できず、データの分布に対してきちんとした対応はしていない
  • VAEやリバーシブルなモデルでは、上データ間の内挿やデータの意味解釈可能な変更のような応用が可能
• メモリ節約の可能性
  • リバーシブルなニューラルネットの勾配計算はメモリが少ない（多い？、すくない？どっち？）、深さに対して線形でなく、定数となる

2. 背景：フローベース生成モデル

$x$ を高次元の確率変数（ベクトル）とし、未知の分布 $x \sim p^*(x)$ に従っているとする。ここからi.i.d でデータセット $\mathcal{D}$ を取得し、パラメータ $\theta$ のモデル $p_{\theta}(x)$ を選択したとする。データ $x$ が離散値であれば、対数尤度では、以下を最小化することになる

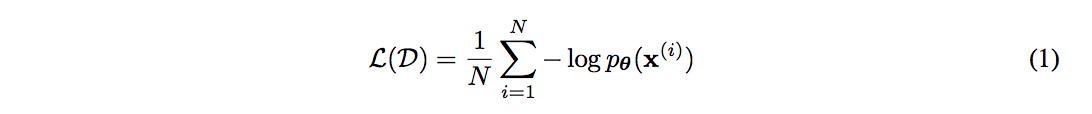
フローベースモデルでは、潜在変数の分布を通して生成

${\bf z}$ は潜在変数を表し、$p_{\theta}({\bf z})$ は多変量正規分布のようなシンプルな
分布。関数 ${\bf g}{\theta}({\bf z})$ は可逆（全単射）であり 、データ $x$ が与えられた時、次のように潜在変数を推定することができる ${\bf z} = {\bf f}{\theta}({\bf x}) = {\bf g}^{-1}_{\theta}({\bf x})$

ここで、${\bf f}$ に注目すると、${\bf f}$ は一連の変換により構成されている：${\bf f} = {\bf f}_1 \circ {\bf f}_2 \circ \cdots {\bf f}_K$ このような $x$ と $z$ の関係は次のように書ける

この可逆でリバーシブルなシーケンスをflowと呼んでいる。(4)を使って変数変換を考えると、生成モデルの確率密度は次のようになる

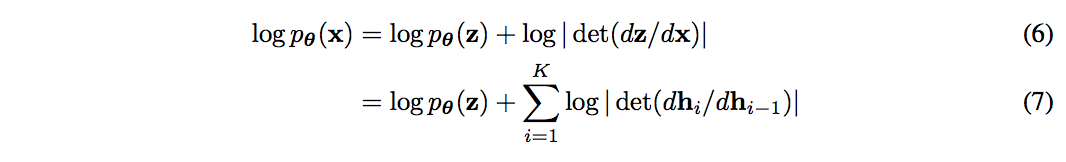
$d{\bf h_i}/d{\bf h_{i−1}}$ はヤコビ行列で、$log|det(d{\bf h_i}/d{\bf h_{i−1}})|$ はヤコビ行列のlog-determinantの絶対値の対数。
$d{\bf h_i}/d{\bf h_{i−1}}$ が三角行列になるような変換を選ぶと、log-determinantの計算は以下の形で非常に楽になる。

結局生成モデルおよび、対数尤度の計算をするためには、生成器各変換において以下が必要

• 関数
• 逆関数
• log-determinant

3. 提案手法

• 提案手法は、NICE、RealNVPを基礎として作られている。
  • NICE: Non-linear Independent Components Estimation
  • Density estimation using Real NVP
• 1ステップは、actnorm - 1 x 1 convolution - coupling layerで構成
• これが組み込まれて繰り返され、提案ネットワークを構成
  • multi-scaleアーキテクチャ。Kのフローの深さとLのレベルを持っている。

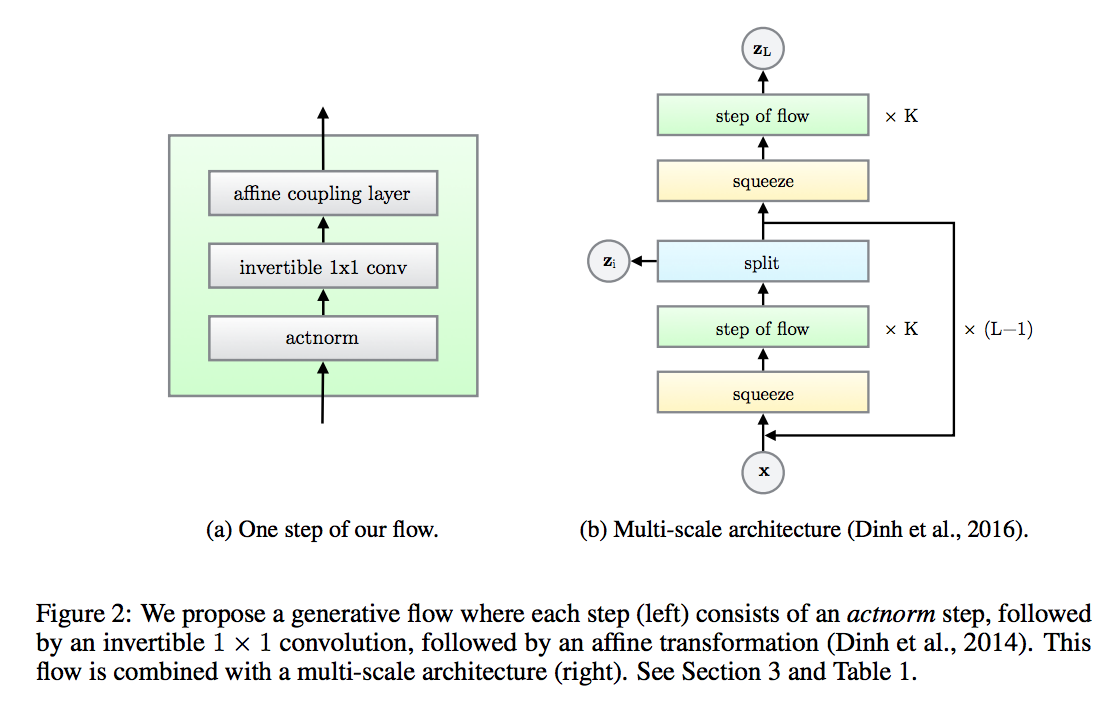
Actnorm

• Dinh et al 2016はバッチ正則化を使っていた
• バッチ正則化は、バッチサイズが小さいとパフォーマンスの低下につながる
• 一方で大きいサイズの画像を使う際は、メモリの制約から、ミニバッチサイズを1にすることもある
• 提案のactnormレイヤ
  • チャンネルごとのスケールとバイアスパラメータを使って、活性化関数にAffine変換を施す
  • チャンネルごとのactnorm通過後の値は、最初のミニバッチを用いて、平均値0、分散1に初期化
  • データ依存型の初期化
  • 初期化後は、スケールとバイアスは普通の学習パラメータとして学習される

Invetible 1 x 1 convolution

• Dinh et al 2014, 2016(NICEとRealNVP)はチャンネルの順序を反転させる操作と同等の処理を含むフローを提案
• 本提案では処理を学習可能で可逆な1 x 1の畳み込み層に置換する
  • 入力と出力のチャンネル数が同じ1 x 1の畳み込み層は、順列の一般化となる
• この畳込み層の重みはランダムな回転行列で初期化される

$h \times w \times c$のテンソル ${\bf h}$ に対する、可逆な1 x 1の畳み込みのlog-determinantは、$c \times c$ の重み行列を用いて以下のように表現できる

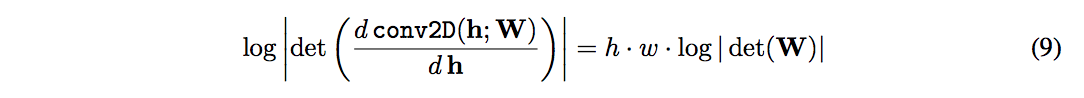
• $det({\bf W})$ の計算量は $O(c^3)$ で、$conv2D({\bf h}; {\bf W})$ の計算量 $O(h \cdot w \cdot c^2)$ としばしば比較される
• ここでの $det({\bf W})$ はランダムな回転行列で初期値しているので、対数行列式の値は$0$。SGDで更新することで0から離れ始める

LU Decomposition

$det({\bf W})$ の計算量 $O(c^3)$ は、LU分解を使って ${\bf W}$ を直接パラメタライズすることで $O(c)$ まで削減することができる

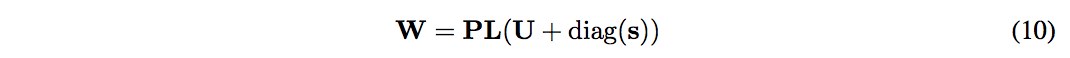
${\bf P}$ は置換行列、${\bf L}$ は対角成分が $1$ の下三角行列、${\bf U}$ は対角成分が $0$ の上三角行列。これにより対数行列式は次のようにシンプルになる

• cが大きくなると、計算コストは非常に大きくなるが、実験ではそんなに処理時間の差はでなかった
• パラメータは、まずWの回転行列をランダムに初期化して、対応する ${\bf P}$（固定）、${\bf L}$、${\bf U}$、${\bf s}$（最適化）を計算

Affine Coupling Layer

• Affine Coupling Layerは、順変換、逆変換、対数行列式が効率的に行える、強力な可逆変換
• Additive coupling layer は、table.1の式で s = 1 の特別な例。

Zero initialization

• Affine coupling layerは、最初恒等関数となるように、ニューラルネットの最後の畳み込み層をゼロで初期化
• これにより非常に深いネットワークでうまく学習できるようになることを実験で発見。

Split and concantenation

split()は、入力テンソル ${\bf h}$ をチャンネル方向に2分割する。これに対して、concat()は、これの反対を行う処理で、1つのテンソルに結合する

Permutation

• 各次元が他のすべての次元に影響を与えることを担保するため、上記フローの各ステップでは、変数のなにかしらの順列変更が先に行われる
• Dinh 2014, 2016では、チャンネルを逆順に並べ替えるのと同等の処理がadditive coupling layerの前に行われていた。
• 固定されたランダムな入れ替えもこの入れ替え方法のひとつ
• 今回の可逆な 1 x 1畳み込みはこれらのような入れ替えの一般化
• 実験ではこれらの比較検証をする