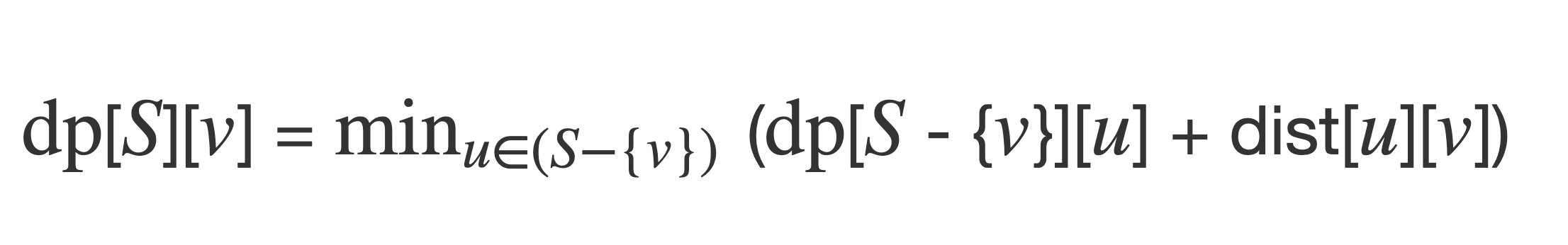競プロで使えそうな基礎的アルゴリズム

#何の記事？

競プロで使えそうなアルゴリズムを羅列してみました。

###※随時更新します
#素数判定（エラトステネスのふるい）

from itertools import accumulate
import math
m = 10**5

L = [x for x in range(2,m+1)]

#エラトステネスのふるいで素数を抽出
for y in range(2, int(math.sqrt(m)+1)):
    L = [z for z in L if(z == y or z % y != 0)]

#N+1/2も素数であるものを抽出
P = []
for w in L:
    if (w+1)/2 in L:
        P.append(w)

#累積和のために作成
G = [0] * (m+1)
for i in P:
    G[i+1] = 1

#累積和
Q = list(accumulate(G))



n = int(input())
for _ in range(n):
    s, t = map(int, input().split())
    print(Q[t+1]-Q[s])




'''
以下の素数判定は遅い。
上のようにエラトステネスの篩を使う

def isPrime(n):

    if n == 1:
        return False
    if n % 2 == 0:
        return False
    for i in range(3, int(math.sqrt(n)+1), 2):
        if n % i == 0:
            return False
    return True

'''

#Bit 動的計画法（巡回セールスマン問題）

この方の記事が超分かりやすいです。

v, e = map(int, input().split())

inf = 10**7
edges = [[inf]*v for _ in range(v)]

for i in range(e):
    s, t, d = map(int, input().split())
    edges[s][t] = d

#Dpは全体集合の部分集合Sについて最後がvであるという制約の下で順序を最適化したときのSの中での最小コスト
dp = [[inf]*v for _ in range(2**v)]
dp[0][0] = 0

#集合（訪れたか訪れていないかを表す二進数）
for x in range(2**v):
    #最後に訪れたノード
    for y in range(v):
        #最後に訪れた以外のノード
        for z in range(v):
            #1.すでに訪れたかどうか 2.最後に訪れたノードではないか 3. yとzはそもそもつながっているのか
            if ((x >> y) & 1) and y != z and edges[z][y] < 10**6:
                dp[x][y] = min(dp[x][y], dp[x^(1<<y)][z]+edges[z][y])

if dp[-1][0] > 10**6:
    print(-1)
else:
    print(dp[-1][0])

#最短経路問題（ベルマンフォード法）

こちらを参考にさせていただきました。
またベルマンフォードに関する解説はこちらの記事がわかりやすかったです。

#v:頂点 e:辺
v, e = map(int, input().split())
#辺を格納するリスト（隣接行列でも隣接リストでもない）
edges = []

for _ in range(e):
    s, t, w = map(int, input().split())
    edges.append([s, t, w])
    # edges.append([t, s, w])

#以下, ベルマンフォード
def bellman_ford(start,goal,edges,v):
    #距離初期化
    distance = [float("inf")] * v
    distance[start] = 0
    
    for i in range(v):
        #距離が更新されたかどうか
        updated = False
        for s, t, w in edges:
            if distance[t] > distance[s] + w:
                distance[t] = distance[s] + w
                updated = True
        #距離が更新されなくなったら、最短経路が求まっている証拠
        if not updated:
            break
        #v回更新しても最短経路の更新が終わらない→負の閉路が存在する
        if i == v - 1:
            return -1
    return distance[goal]

for i in range(v):
    print(bellman_ford(0, i, edges, v))

#最大流問題（フォード・ファルカーソン）

こちらの記事がわかりやすい
そのうち実装します...

#8クイーン問題（バックトラック）

・最初の一つだけ表示ver

row = [0] * 8
col = [0] * 8
dpos = [0] * 15
dneg = [0] * 15

def row_search(a):
    for i in range(8):
        if col[i] == 0 and dpos[a+i] == 0 and dneg[a-i+8-1] == 0:
            row[a] = i
            col[i] = 1
            dpos[a+i] = 1
            dneg[a-i+8-1] = 1
            if a == 7:
                return "Success"
            else:
                if row_search(a+1) == "Success":
                    return "Success"
                else:
                    row[a] = 0
                    col[i] = 0
                    dpos[a + i] = 0
                    dneg[a - i + 8 - 1] = 0
    return "解なし"

row_search(0)

for i in row:
    l = ["-"]*8
    l[i] = "*"
    print(" ".join(l))

・全て表示ver

row = [0] * 8
col = [0] * 8
dpos = [0] * 15
dneg = [0] * 15

def row_search(a):
    for i in range(8):
        if col[i] == 0 and dpos[a+i] == 0 and dneg[a-i+8-1] == 0:
            row[a] = i
            col[i] = 1
            dpos[a+i] = 1
            dneg[a-i+8-1] = 1
            if a == 7:
                print("==================================")
                for i in row:
                    l = ["-"] * 8
                    l[i] = "*"
                    print(" ".join(l))

            else:
                row_search(a+1)
            row[a] = 0
            col[i] = 0
            dpos[a + i] = 0
            dneg[a - i + 8 - 1] = 0


row_search(0)