導入
競技プログラミングではしばしば、グラフに関するが現れます。特にAtCoderにおいてはAtCoder Beginner Contest（以下、「ABC」とかく）のC問題でも登場することがあり、グラフ理論に触れたことがない方にとっては、一種の鬼門になっているのではないかと思います。
グラフと聞くと、「数学的で難しそう」「見たことはあるけど使い方が分からない」と感じる方も多いかもしれません。しかし、グラフ理論は実はとても実用的で、身の回りのさまざまな問題をモデル化できる強力なツールです。例えば、人間関係やインターネットの構造、道路網、ゲーム内のマップなど、実世界の「関係性」や「つながり」は、ほとんどがグラフで表現できます。競技プログラミングにおいては、「連結判定」「最短経路」「閉路検出」など、基本的なグラフアルゴリズムを知っているだけで、特に、灰色、茶色コーダーにとって大きなアドバンテージになります。
この記事では、グラフについて初めて学ぶ方に向けて、グラフとはどのようなものなのか、という部分について、詳細に解説していこうと思います。不明瞭な点がありましたら、コメントで教えていただけると幸いです。
グラフとは
グラフとは、「点（頂点, vertex, node) と、それらを結ぶ 線（辺, edge）」の集合です。
- 頂点の集合：$V$
- 辺の集合：$E$
として、グラフ $G = (V,E)$と表します。
今から考えるグラフは２つの要素間の関係について考えるので、各点と、ふたつの点を結ぶ辺によってつくられた状態を考えます。
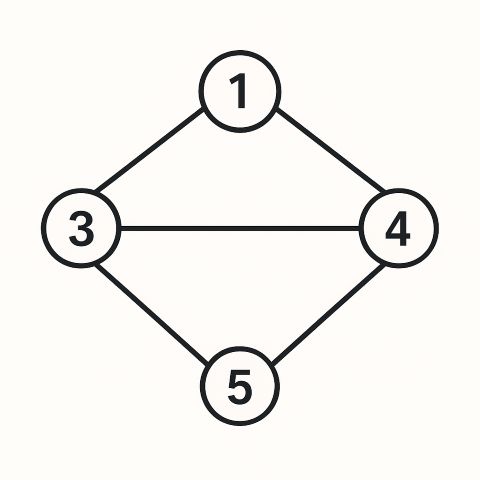
以下はグラフの例です。
（ChatGPT 4oに出力してもらいました。なぜ2がないんだ。）
例として、頂点1について注目すると、
2本の辺が接続しており、頂点3、4と結ばれていることがわかります。
グラフは、身近な事柄に置き換えて考えることができます。
たとえば人間関係に例えると、各頂点は個々の人を、辺はその人同士の交友関係を表していると考えられます。
グラフで使われる用語
有向グラフと無向グラフ
-
有向グラフ
有向グラフとは、各辺に方向があるグラフのことです。たとえば、SNSにおけるフォロー／フォロワーの関係は、有向グラフで表すことができます。フォローしている人からフォローされている人へ向かって辺が伸びていると考えると、関係性の一方向性を表現できます。 -
無向グラフ
無向グラフとは、辺に方向がないグラフのことです。たとえば、SNSにおける相互フォローの関係は無向グラフで表すことができます。フォローし合っているユーザー同士の関係には方向性がないため、双方向のつながりとして扱われます。
単純グラフと多重グラフ
2つの頂点の間に複数の異なる辺が存在する場合、それらを多重辺と呼び、そうした辺を含むグラフを多重グラフといいます。
一方、同じ2頂点間に1本以下の辺しか存在しないグラフを単純グラフと呼びます。
隣接
ある頂点とほかの頂点が辺でつながっていることを隣接しているといいます。
- 無向グラフ：AとBがつながっていれば、AもBもお互いに隣接しています。
- 有向グラフ：A→Bのとき、AはBに隣接しているが、BはAに隣接しているとは限らない。
次数
- 次数（degree）とは、ある頂点に接続している辺の数です。
無向グラフ：
- 次数は単純に「何本の辺がつながっているか」。
- 例：Aさんは、BさんとCさんの２人と友達である。 → Aの次数は2。
有向グラフ：
- 入次数（in-degree）：その頂点に向かってくる辺の数
- 出次数（out-degree）：その頂点から出ていく辺の数
- 例：Aさんは、BさんとCさんの２人が友達だと思っている。 →Aの出次数は２
Bさんは実はAさんを友達と思っていなかった。 →Aの入次数は１
経路
経路（path） とはある頂点から別の頂点まで移動するルートのことです。
例として、先ほど挙げた図を用います。
このグラフにおいて、頂点１から５まで移動する経路を考えると、
１→３→５、１→４→５、１→３→４→５のような経路が考えられます。
基本的には、同じ頂点を２度通らないものを指しますが、厳密に定義するために単純経路と呼ばれることがあります。
連結
連結は無向グラフと有向グラフで定義が少し異なります。
無向グラフから見ていきましょう
無向グラフの連結：
- 無向グラフで、どの2つの頂点の間にも経路が存在するとき、そのグラフは「連結」と呼ばれます。
- 逆に、ある2頂点間に経路がなければ、「非連結」となり、グラフはいくつかの連結成分に分かれています。
有向グラフの連結：
有向グラフの連結には２つのパターンがあります。
- 強連結（Strongly Connected）
- 弱連結（Weakly Connected）
回路・閉路
回路、閉路はともに「ある頂点から出発して、再びその頂点に戻ってくるような経路のこと」を指すが、文献ごとにその定義は異なる。
ここでは、回路（サーキット, circuit） は同じ辺を通らずにもとの頂点に戻ってくるような経路（同じ頂点は何度通ってもよい）、閉路（サイクル, cycle） は、同じ頂点を２度通らない（＝ 単純パス である）経路として定義します。
木
無向グラフにおいて、
閉路を持たず、連結であるようなグラフを木（Tree） といいます。
あまり、競技プログラミングで見かけることは少ないですが、次数が１である頂点を葉（leaf） といい、木を連結成分とするグラフを森（Forest） といいます。
グラフの表現方法
グラフは以下の３つの方法で表現が可能です。
| 表現方法 | 特徴 | 主な用途・利点 |
|---|---|---|
| ① 隣接行列 | 2次元配列 | 辺の存在判定が高速（O(1）） |
| ② 隣接リスト | 配列＋リスト | メモリ効率が良く、辺の探索が速い |
| ③ 辺リスト | 辺の一覧 | 辺中心のアルゴリズム（Kruskalなど）で便利 |
現段階では、複数の表現の種類があるということを念頭に置いてもらえれば大丈夫です。
① 隣接行列（Adjacency Matrix）
- $N \times N$ の2次元配列
adj[i][j]を使う -
adj[i][j] = 1なら、頂点 $i$ から $j$ に辺があることを表す - 無向グラフなら、
adj[i][j]=adj[j][i]である。
# 無向グラフ（例: 0-1, 1-2に辺）
adj = [
[0, 1, 0],
[1, 0, 1],
[0, 1, 0]
]
長所：
- 辺の有無を $O(1)$ で判定できる
- 実装がシンプル
短所：
- メモリ消費が $O(N^2)$ と大きい（頂点が多いと不利）
② 隣接リスト（Adjacency List）
- 各頂点ごとに、隣接する頂点のリストを記録
# 無向グラフ（0-1, 1-2）
adj = {
0: [1],
1: [0, 2],
2: [1]
}
長所：
- メモリ効率が良い（辺の数 MM に比例）
- 実際の探索（DFS・BFSなど）に向いている
短所：
-
iとjの間に辺があるかを調べるために、リストを操作する必要がある。
辺の数が膨大であるときは、タイムロスである。
③ 辺リスト（Edge List）
- 辺を（出発点, 到達点）で記録したリスト
- 重み付きグラフなら（出発点, 到達点, 重み）の形
# 有向・重み付きグラフの例（0→1:重み2, 1→2:重み3）
edges = [
(0, 1, 2),
(1, 2, 3)
]
長所：
- ソート・Union-Find・Kruskal法などのアルゴリズムに便利
- 実装が直感的
短所：
- 隣接情報の取得や探索には向かない
これらのデータ構造の向き不向きはアルゴリズムによって異なる。各アルゴリズムでの解説にて詳細に説明する。
まとめ：グラフの基礎
今回は、グラフの基本的な概念と用語、表現方法について学びました。
- グラフとは「頂点」と「辺」からなる構造で、現実世界の関係性を抽象的に表現できる。
- 有向グラフ・無向グラフ、多重グラフ・単純グラフといった分類がある。
- 頂点のつながり（隣接）や次数、経路や連結性、閉路や木の構造など、基本用語を把握。
- グラフのデータ構造として、隣接行列・隣接リスト・辺リストの3種類がある。
ここまでお読みいただき、ありがとうございます。
内容に誤りや不明瞭な点がございましたら、コメントにてご指摘いただけますと幸いです。
以下、更新記録です。
2025/06/04: 記事の構成を変更しました。導入部分を追記しました。