シミュレーテッド・アニーリング(Simulated Annealing、以下SA)は、「焼きなまし法」とも呼ばれ、大域的最適化問題へのアプローチ方法の一つです。「焼きなまし」の名称から察せられる通り、金属を高温の状態にして、徐々に温度を下げることで秩序がある構造を作り出す焼きなましの技術をコンピュータ上で再現したアルゴリズムになります。
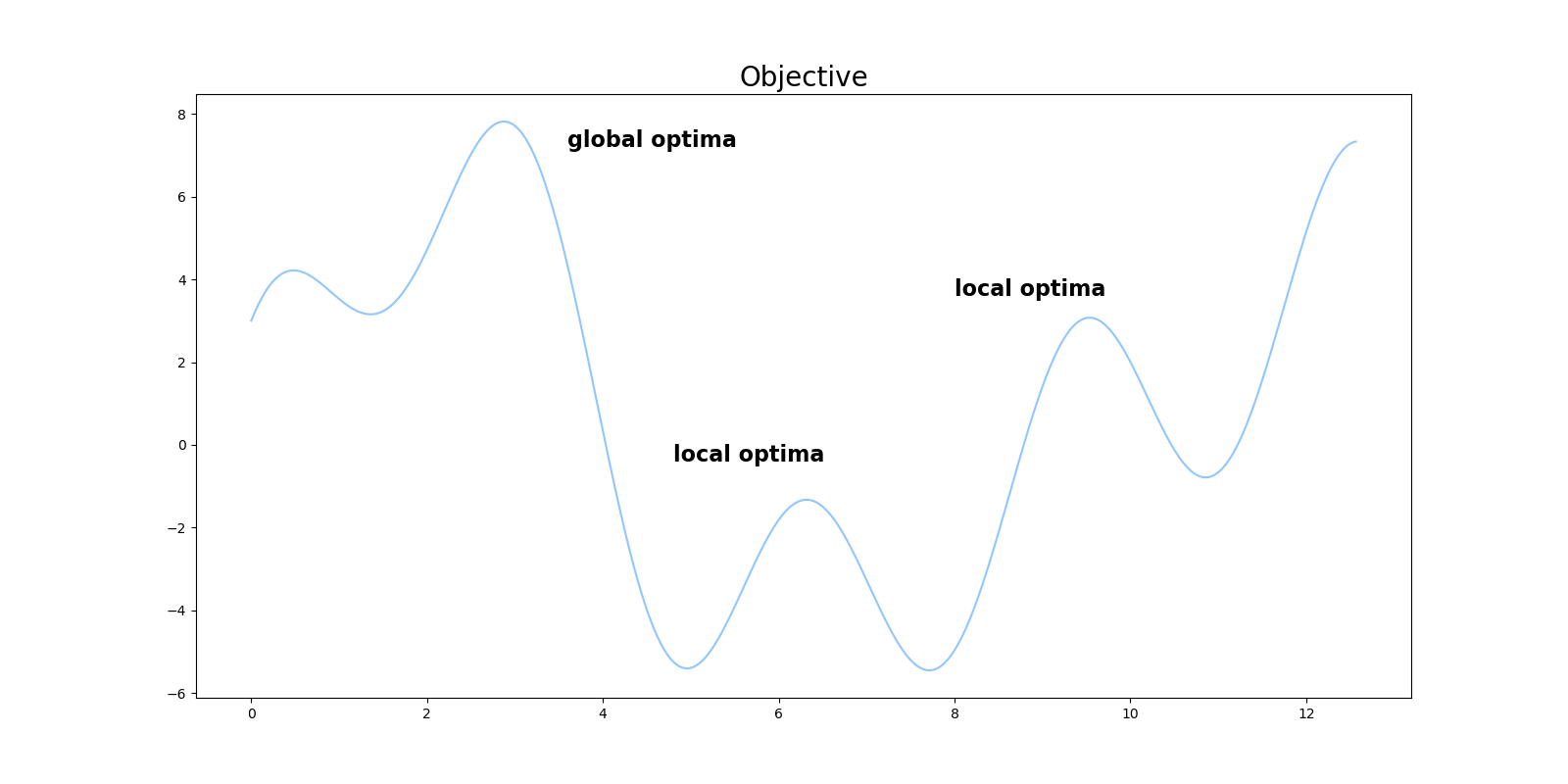
最適化問題では、最適解に到達する前に局所解にはまってしまい、大域的な最適解に到達できないケースがしばしば問題になります。下図の例では、$x=9$や$x=6$付近の局所最適解にはまらずに、$x=3$付近の大域的最適解に到達するのが目標になります。
この記事では、SAをゼロから実装してみることで、SAに対する理解を深めることを目的とします。
アルゴリズム
SA法では以下のような手順で探索を行なっていきます。
- 初期温度を設定する
- 初期値をサンプリングする
- 温度を下げる
- ランダムに次の点をサンプリングする
4.1. ランダムにサンプルした点が現在の点よりも良かったら、現在の点を更新する
4.2. ランダムにサンプルした点が現在の点よりも悪くても、温度に依存する一定確率で現在の点を更新する - 3~4を繰り返す
3の温度を下げる方法は、たとえば次のような関数が使われます。
T = 1.
cooling_rate = 0.9
def cool(T): return cooling_rate * T
T = cool(T)
試行回数を増やすたびに温度が下がっていけば問題ないので、次のような方法でもSA法で使うことができます。
T = 1.
n_iter = 100
for iter in range(n_iter):
T = T / (iter + 1)
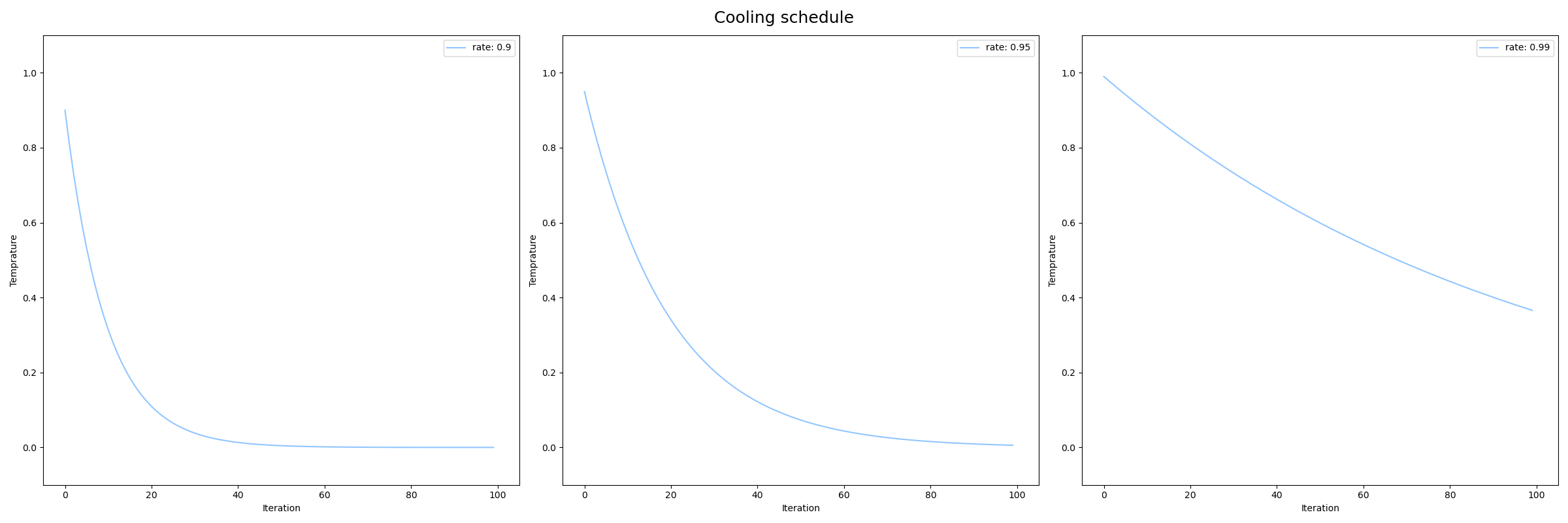
一つ目の例で、cooling_rate=0.9, 0.95, 0.99における温度$T$のグラフは次のようになります。
次に4.2の「 ランダムにサンプルした点が現在の点よりも悪くても、温度に依存する一定確率で現在の点を更新する」についてですが、この操作によってSA法は局所解にトラップされるのを回避しています。
単純に現在の解より新しい解の方がよければ更新するだけでは、局所的な解にたどりついてしまうとその後に値を更新することができません。そこで、一定確率で改悪する方向に値を更新することで、局所解からの脱出を可能にします。
しかしながら、常に一定確率で改悪を許してしまうと局所解の中心付近の探索に時間がかかり、計算コストが大きくなってしまいます。SA法では、温度$T$に依存する形で、温度$T$が下がるにつれて改悪されにくくしていきます。
U(0, 1) > \exp{(-\frac{\Delta{E}}{T})}
$U(0,1)$は区間0から1の一様分布で、$\Delta{E}$は現在の点と新しい点の差です。式から分かる通り、温度$T$が小さくなるにつれて、上式が成り立ちにくくなっていきます。この手法をMetropolis法と呼びます。
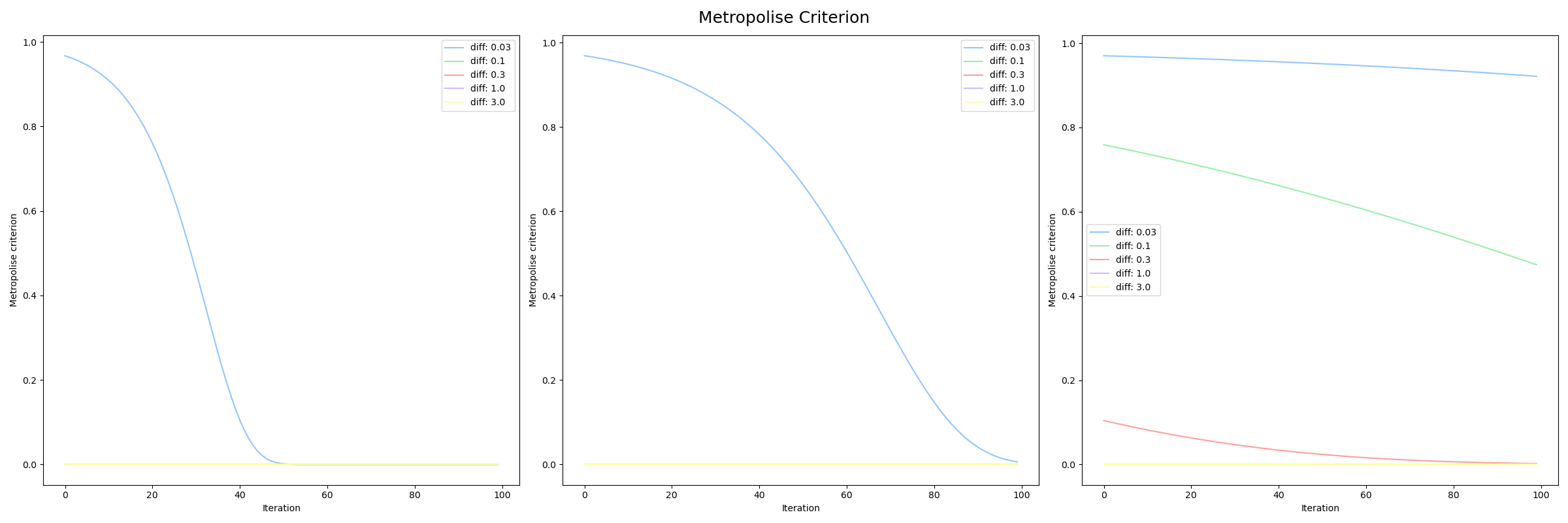
cooling_rate=0.9, 0.95, 0.99における提案された探索点の採択率は次のグラフのようになります。冷却率が低い(cooling_rate=0.99)場合は、新しい点と現在の点の差分が大きくても採択する確率が他の2つより全体的に高くなっています。また、cooling_rate=0.9, 0.95, 0.99の全ての場合で冷却が進むにつれて、改悪される確率は低くなっていっています。
実装
今回最大値を探索する関数には、次の関数を設定します。
f(x) = 2\sin{(x)}+3\cos{(2x)}+5\sin{(\frac{2}{3}x)}
SA法で目的関数の最大値を見つけるプログラムを実装します。探索の初期値には、$x=8$付近を設定します。
def objective(x):
return 2 * np.sin(x) + 3 * np.cos(2 * x) + 5 * np.sin(2 / 3 * x)
n = 10000
data_x = np.linspace(0, 4 * np.pi, n)
data_y = objective(data_x)
def simulated_annealinng(objective, cooling_rate, n_iter):
x_iter = np.zeros((n_iter, ))
obj_iter = np.zeros((n_iter, ))
# set initial temperature and cooling schedule
T = 1.
def cool(T): return cooling_rate * T
# set initial index to 7000,
# because this point is around minima
index = 7000
curr_x = data_x[index]
curr_obj = objective(curr_x)
best_x = curr_x
best_obj = curr_obj
for i in range(n_iter):
# decrease T according to cooling schedule
T = cool(T)
index = np.random.choice(n, 1)
new_x = data_x[index]
new_obj = objective(new_x)
# update current solution iterate
if (new_obj > curr_obj) or (np.random.rand()
< np.exp((new_obj - curr_obj) / T)):
curr_x = new_x
curr_obj = new_obj
# Update best solution
if new_obj > best_obj:
best_x = new_x
best_obj = new_obj
# save solution
x_iter[i] = best_x
obj_iter[i] = best_obj
return x_iter, obj_iter
x_iter, obj_iter = simulated_annealinng(
objective, cooling_rate=0.9, n_iter=100)
best_index = np.argmax(obj_iter)
print("best x: {}, best objective: {}".format(
x_iter[best_index], obj_iter[best_index]))
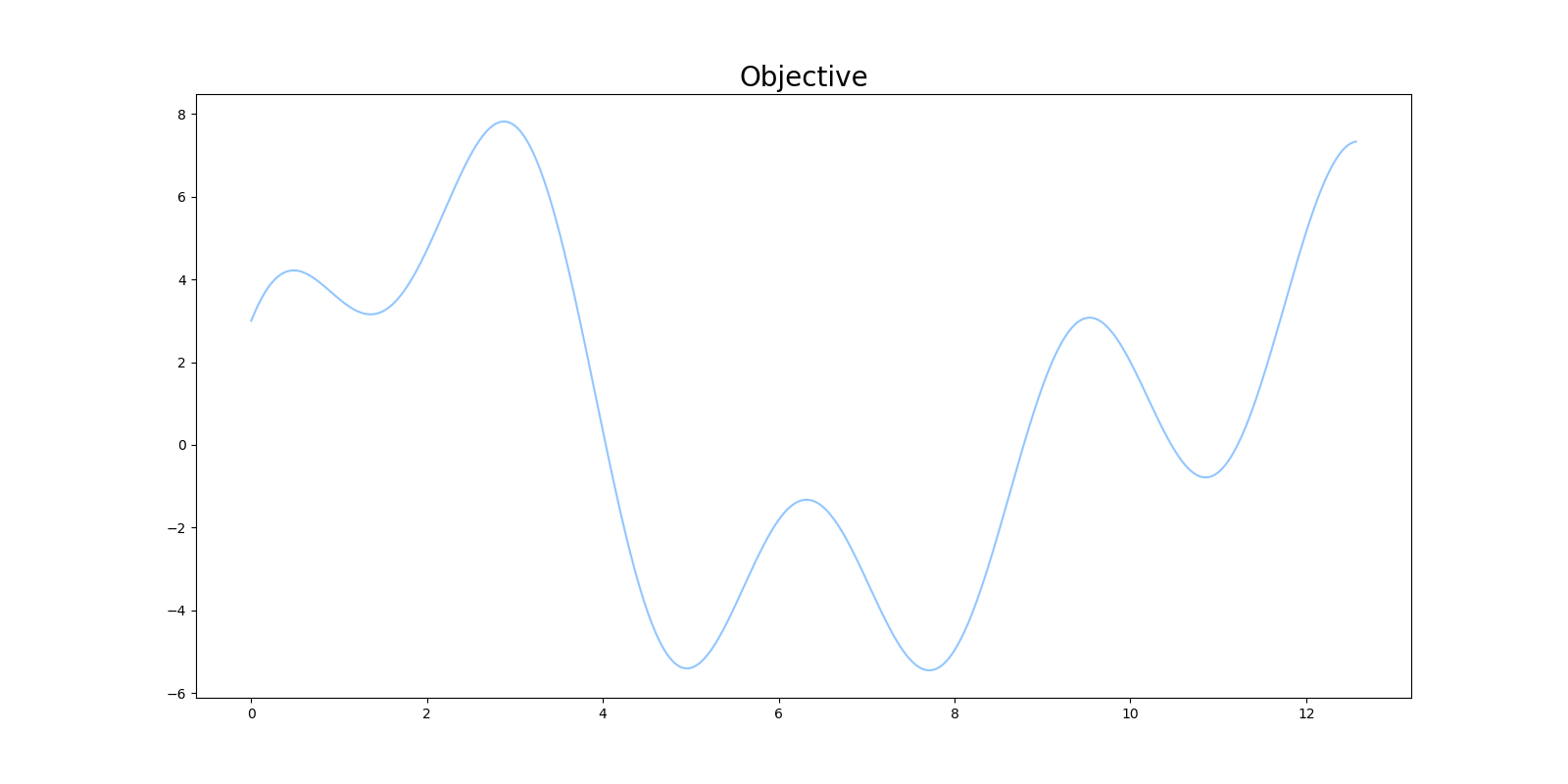
局所解をうまく避けながら、大域的最適解に到達することに成功しています。
プログラムをから察せられる通りSA法の実装は比較的簡単であり、局所解からの脱出が可能であるため、有用なアルゴリズムと言えます。しかしながら、計算量が多く解空間が広くなればなるほど計算コストが肥大化してしまう点や、探索結果がパラメータ(特に冷却率)に大きく依存し、問題設定ごとにパラメータの試行錯誤による調整が必要となるといった問題点が存在しています。
まとめ
SA法をゼロから実装して、関数の最大値を見つける実験を行いました。
他のベイズ最適化などの最適化アルゴリズムと比べると比較的理解しやすかったです。
今回実装したコードはこちらのレポジトリにあります。