はじめまして。まーもんと申します。
絶対にアドベントカレンダーでやる事ではないと思いますが、他に書ける内容も無いのでこれでいきます。
機械学習のcategorical feature encodingについて3年前の2016年にある論文が出されました。
この技術について日本語で紹介されているものは非常に少ないし、実際の論文の内容について書かれた記事もあまり無いように見えます。
なので、今回はまず、その論文の日本語翻訳に挑戦してみようと思います。(本当は要約したりコーディングしながら説明する方が良さそうですが、時間が足りず)
論文のある場所:http://arxiv.org/abs/1604.06737
※私自身そこまで深い知識を有している訳でも、英語が得意な訳でも、機械学習エンジニアという訳でも無いので間違いを多分に含んでいます。そしてWikipedia等の情報を丸呑みにしながら書いています。間違っていると思ったらどんどん指摘してください。
Entity Embedding of Categorical Variables
ざっくり言えば「カテゴリ特徴量のコーディングにEmbedding(自然言語処理の技術)を応用してみた」って感じです。
イントロダクション
この15年間で、コンピュータの高速化や多くのデータ、手法の改善によってニューラルネットワークの分野は多くの進歩を遂げました。そして、ニューラルネットワークはコンピュータビジョンや、音声認識、自然言語処理に革新を起こし、それぞれの分野を牽引する存在になっています。
しかし、構造化データにおけるニューラルネットワークの優位性は上記の分野ほどではありません。これはKaggleのコンペティションで優勝している多くのチームがニューラルネットワークよりも決定木モデルをより多く使っている事からわかります。
このことを理解するために、決定木モデルとニューラルネットワークを比較しましょう。機械学習の一般的な問題は

という関数に近似することができます。これは入力データ(x1, x2, ..., xn)が与えられた時に目的変数yを生成するということです。
主要なニューラルネットワークはこの関数を任意の連続関数や区分的連続関数に近似します。しかし、一定レベルの連続性を前提としているので、任意の非連続関数に近似することは適切ではありません。トレーニング段階では、データの連続性は最適化の収束を保証し、予測の段階では、入力の値をわずかに変更しても出力を安定させることができます。一方で、決定木モデルは特徴量の連続性を前提とせず、必要に応じて変数の状態を細かく分割できます。
おもしろいことに、自然の中で得られる多くのデータは、正しく処理する事で連続的に表現できます。そして、データの連続性を明らかにした時は、ニューラルネットワークがデータを学習する能力は向上するのです。例えば、畳み込みニューラルネットワークが同一近傍ピクセルをグループ化することを考えます。これは単純に画像データのピクセルを平坦ベクトルで表現するよりも、データの連続性を向上させています。自然言語処理の分野におけるニューラルネットワークの向上はWord Embeddingと言われる、似たような意味を持つ単語を単語空間上で互いに近づけ、それによってOne-Hot Encodingよりも高い言葉の連続性を表現できることに基づいています。
自然に見つかる非構造化データとは異なり、カテゴリー特徴量を含んだ構造化データは連続性をもたなかったり、明らかではないことがあります。ニューラルネットワークの連続性は、これらカテゴリー特徴量への適用性を制限します。したがって、カテゴリー特徴量を整数で表現した構造化データにニューラルネットワークを適用することは単純にはうまく機能しません。この問題を解決する最も基本的な方法はOne-Hot Encodingですが、これには二つの欠点があります。一つ目はカテゴリーの種類が非常に多い特徴量を扱う場合、非現実的なコンピュータリソースを要求することです。二つ目はカテゴリ間の相互関係を扱えず、有益な関係性を無視してしまうことがあることです。
この論文ではthe Entity embeddingを用いて、Eq.(1)の関数近似問題において互いに類似した性質を持つ値を互いに近づける多次元空間におけるカテゴリー特徴量の表現を自動的に学習する方法を示します。そして、これにより、データの本質的な連続性が明らかになり、ニューラルネットワークや他の一般的な機械学習アルゴリズムが問題を解決するのに役立ちます。
Entityの表現はこれまでもたくさん述べられてきました。この論文での主な役割は次の通りです。まず、一般的な関数近似問題でこの考えを発展させ、大きな機械学習のコンペティションでその力を実証しました。次に、学習したEmbeddingの特性を調べ、Embedding::を使用してカテゴリデータを理解し視覚化する方法を示しました。
関連研究
我々の知る限りでは最初にEntity Embedding法がニューラルネットワークに用いられたのはリレーショナルデータの表現についてである。最近では、複雑なリレーショナルデータを含んだ大規模なナレッジデータベースにおいてEntity embeddingを使って多くのworksを見ることもある。リレーショナルデータの基本的な構造は、hとtをEntityとし、rを関係とした(h,r,t)の表現(Triplet)をとる。Entityはベクトルと関係rによる単一の行列、二つの行列または同じEmbedding空間においてEntityとして単一のベクトルで表現するなどの様々な方法で表現される。このTripletのような様々な種類の評価関数は、Embeddingを評価する目的関数として使われるように定義されている。
自然言語処理において、Word Embeddingは単語やフレーズを意味空間(semantic space)上の連続した分散ベクトルにマッピングするものとして使われる。この空間上では似ている言葉はより近くにあるように表現されている。これのより興味深い点は言葉の距離は意味だけでなく、異なるベクトルの向きも含んでいると言う事である。例えば、以下のような関係を明らかにすることができる。

Word Embeddingを学習する方法は様々存在する。とても高速な方法は、単語の文脈を以下の値を最大化するためにWord Contextを利用することである。

ここで、 は
は![]() のコンテキストウィンドウに
のコンテキストウィンドウに![]() が含まれている確率
が含まれている確率 のベクトル表現である。分母のSumは全ての語彙に対して行われる。Word Embeddingは教師あり学習によって学習することもできる。例えばRef.では感情をラベル付されたテキストを使って学習を行う。この方法はこの論文内で用いられる手法とかなり近いが、異なるコンテキストを用いている。
のベクトル表現である。分母のSumは全ての語彙に対して行われる。Word Embeddingは教師あり学習によって学習することもできる。例えばRef.では感情をラベル付されたテキストを使って学習を行う。この方法はこの論文内で用いられる手法とかなり近いが、異なるコンテキストを用いている。
Tree Based Methods
- Single decision tree
- Random forests
- Gradient boosted trees
以上のtree based methodsが紹介されているが、あまり関係がないので割愛します。
Structured data(構造化データ)
構造化データとは、様々な特徴(変数)または目的変数を表す列と異なるサンプルを表す行によって表されたデータのことである。この論文ではこの種類のデータに焦点を当てる。
構造化データで最も一般的な変数タイプは、連続変数と離散変数である。例えば、温度、価格、重量などの連続変数は実数で表すことができ、年齢、色、バス路線番号などの離散変数は、整数で表すことができる。この整数は単にラベル付けのために便宜上使われるだけであり、その数値自体に意味を持たない。例えば、赤、青、黄を1,2,3の数字を用いて表現した際に、「青は赤よりも大きい」や「赤と黄と青の平均」などの数値の情報を基に情報を追加する場合である。こういった整数値はNominal number(名目番号、公称数)と呼ばれる。また、整数インデックスには年齢や暦などの固有の順序がついているものもある。こういった整数はCardinal number(基数)やOrdinal numbers(序数)と呼ばれる。
ここで、意味や順序について考えることは整数を単にNominal numberとして考えることよりも、効果的では無い場合があることに注意しなければならない。例えば、月の順序はその月の日数とは何も関係が無い(1月の日数は2月よりも6月の方が近い)。よって、これら両方のタイプの離散変数は同じように扱う。Entity embeddingは関数の出力が似ている離散変数を多次元空間上の近い点としてマッピングすることである。
Entity embedding
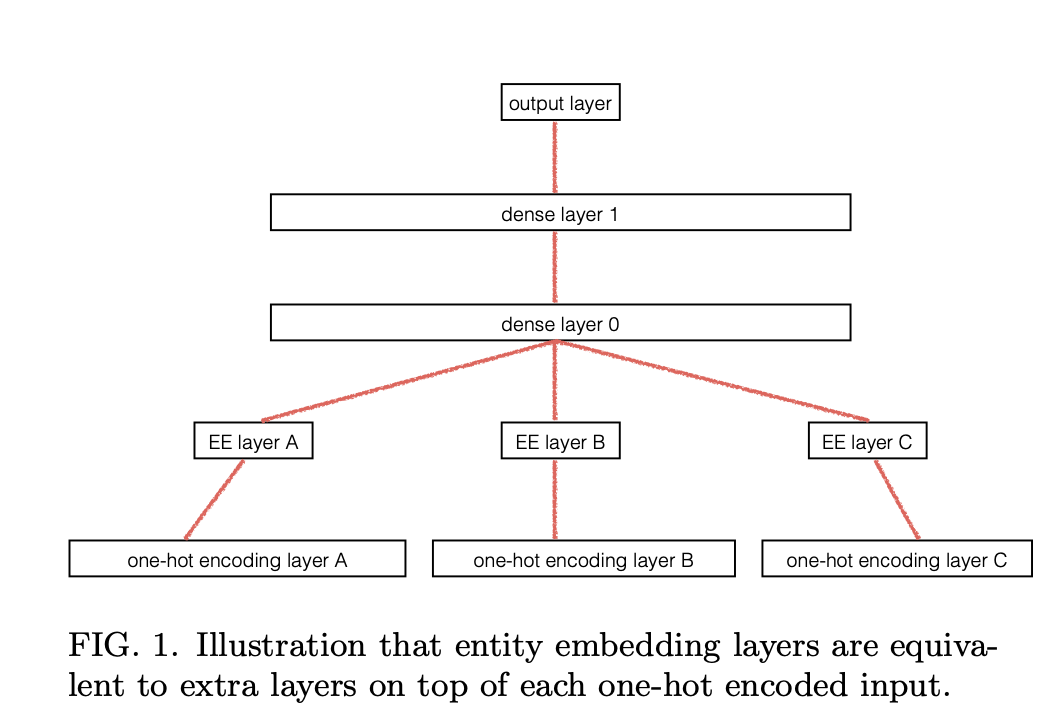 まず、離散変数の各状態を以下のベクトルにマッピングする。
まず、離散変数の各状態を以下のベクトルにマッピングする。
 このマッピングはFig.1においてEE layerとして表されている。これを示す為に
このマッピングはFig.1においてEE layerとして表されている。これを示す為に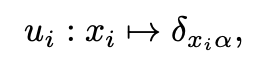 と表す。ここで
と表す。ここで ということである。
ということである。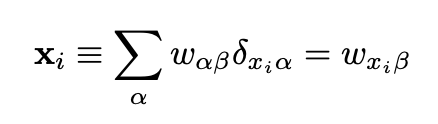 で与えられ、
で与えられ、A.Relation with embedding of finite metric space
距離空間とEmbeddingの関係について語られているが割愛する。
Experiment
この論文ではデータセットとしてKaggleの Rossmann Sale Prediction competitionを例として用いている。(https://www.kaggle.com/c/rossmann-store-sales/data) このコンペティションの目的はDirk Rossmann GmbH(以後「Rossmann」と略す)のそれぞれの店舗での日毎の売り上げを可能な限り正確に予測することである。z
Rossmann hostsによって作られたこのデータセットは二つに分けられている。一つ目はtrain.csvで1115の異なるRossmann storesの1日あたりの売り上げデータの2.5年分であり、合計で1017210の記録である。二つ目はstore.csvで、1115の店の更なる詳細な情報が乗っている。
hostによって作られたデータの他に、外部データがコンペティションフォーラム上で共有されている。多くの特徴量がコンペティション参加者によって与えられている。例えば、Kaggleユーザーのdune_dwellerはstore open変数をドイツの州の休日および学校の休日のカレンダー情報と創刊させることで各店舗が属するドイツの州をスマートに表現した(ドイツでは州ごとに学校や州の休日が異なる)。他の一般的な外部データは天気データやGoogleのトレンドデータ、そしてスポーツのイベントデータなどである。(https://www.kaggle.com/c/rossmann-store-sales/discussion/17048)
受賞した方法では、上記のデータのほとんどを利用したが、この論文の目的は、様々な機械学習の方法を比較することであり、最良の結果を得る事では無い。よって簡単の為に、特徴量の少ない小さなサブセット(表1を参照)のみを使用し、他のいかなる特徴量エンジニアリングを行わないこととする。

このデータセットの90%をトレーニングデータとし、10%をテストデータとする。データの時間的構造をのこす分割(最初の90%の日程をトレーニング用に使用)と、training-test splitが適用される前にランダムにシャッフルされたデータの両方を用いる。シャッフルされたデータの場合、テストデータはトレーニングデータと同じ統計分布を共有することになる。より具体的には、Rossmannデータセットには特徴量がサンプル数より比較的少ない傾向があるので、特徴空間におけるテストデータの分布は、トレーニングデータの分布によって十分に表現できる。シャッフルデータは純粋な統計予測精度に関するモデルのパフォーマンスを測る基準として有用である。時間ベースに分割されたデータ(シャッフルされていないデータ)の場合、テストデータはトレーニングデータから見て未来のデータであり、テストデータの統計的分布は必ずしもトレーニングデータのものと同じでは無い。よって、トレーニングデータから学習したモデルの一般性を測る尺度として使うことができる。
この実験で用いたコードはgithub repositoryにある。
(https://github.com/entron/entity-embedding-rossmann)
ニューラルネットワーク
この実験ではOne-Hot-EncodingとEntity embeddingの両方を利用して、ニューラルネットワークの入力特徴量を表現する。二つのfully connected layers(それぞれ1000と500のニューロンを用いる)をEmbedding layerの上、またはOHC層の上に直接使うことにする。fully connected layerはReLU関数を用いる。
出力層には、シグモイド活性化関数ををもつニューロンが含まれている。ドロップアウトは、結果が改善されなかった為使用していない。
他の方法との比較
Embedding空間上の分布
力尽きる