PyTorchのチュートリアル(Deep Learning with PyTorch: A 60 Minute Blitz)の中のNeural Networksに取り組んだところ、DeepLearning初心者には少々分かりづらいところがあり躓いたので、ここにまとめておきます。
次のチュートリアル「Training a classifier」はこちら。
PyTorchドキュメントやGitHubのソースコードを参考にして、元々のチュートリアルのコードにコメントを加えています。少しだけコードを追加しているところもあります。
細かくコメントを入れてあるので冗長ですが、私と同じように躓いた人の参考になれば幸いです。
尚、公式ページの日本語翻訳ではありませんので悪しからず。
シンプルに日本語翻訳を読みたい方はこちらのサイトに載っています。
モジュールのインポート
import torch as t
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F
Define the network
2つの畳み込み層と3つの全結合層を持つCNNを実装する(画像は公式ページより)
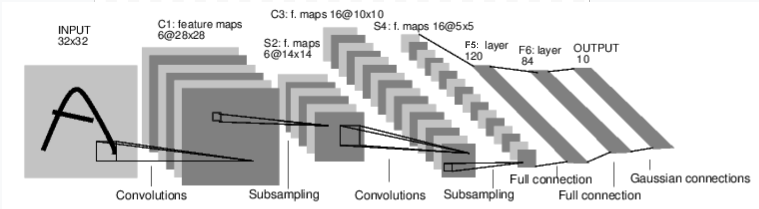
尚、Conv2dはデフォルトでstride=1,padding=0、MaxPool2dはデフォルトでstride=kernel_size,padding=0なので、マップ一枚の縦の長さは畳み込み層を通る度に-4、プーリング層を通る度に1/2となる
今回は2つの畳み込み層と2つのプーリング層により32→28→14→10→5となり、全結合層に渡される時には5*5のマップになっている
class Net(nn.Module):
def __init__(self):
#親クラスのnn.Moduleのコンストラクタを呼ぶ
super(Net,self).__init__()
#畳み込み層を定義する
#引数は順番に、サンプル数、チャネル数、フィルタのサイズ
self.conv1=nn.Conv2d(1,6,(5,5))
#フィルタのサイズは正方形であればタプルではなく整数でも可(8行目と10行目は同じ意味)
self.conv2=nn.Conv2d(6,16,5)
#全結合層を定義する
#fc1の第一引数は、チャネル数*最後のプーリング層の出力のマップのサイズ=特徴量の数
self.fc1=nn.Linear(16*5*5,120)
self.fc2=nn.Linear(120,84)
self.fc3=nn.Linear(84,10)
def forward(self,x):
#入力→畳み込み層1→活性化関数(ReLU)→プーリング層1(2*2)→出力
x=F.max_pool2d(F.relu(self.conv1(x)),2)
#入力→畳み込み層2→活性化関数(ReLU)→プーリング層2(2*2)→出力
x=F.max_pool2d(F.relu(self.conv2(x)),2)
#ここまでの出力を全結合層へ繋げるために1次元へ展開
#-1を引数とすることで、self.num_flat_features(x)の値から自動的に値が決まる(ここでは結局1になる)
x=x.view(-1, self.num_flat_features(x))
#入力→全結合層1→活性化関数(ReLU)→出力
x=F.relu(self.fc1(x))
#入力→全結合層2→活性化関数(ReLU)→出力
x=F.relu(self.fc2(x))
#入力→全結合層3→出力
x=self.fc3(x)
return x
def num_flat_features(self,x):
#Conv2dは入力を4階のテンソルとして保持する(サンプル数*チャネル数*縦の長さ*横の長さ)
#よって、特徴量の数を数える時は[1:]でスライスしたものを用いる
size=x.size()[1:]
#特徴量の数=チャネル数*縦の長さ*横の長さを計算する
num_features=1
for s in size:
num_features*=s
return num_features
作成したNNのインスタンスを生成
net=Net()
print(net)
Net(
(conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
(conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
(fc1): Linear(in_features=400, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=84, bias=True)
(fc3): Linear(in_features=84, out_features=10, bias=True)
)
パラメータを確認する
# net.parameters()をリストに型変換することでパラメータを取り出せる
params=list(net.parameters())
# len(params)はパラメータの種類の数
# 今回は、conv1の重み、conv1のバイアス、conv2の重み、conv2のバイアス、fc1の重み、fc1のバイアス、fc2の重み、fc2のバイアス、fc3の重み、fc3のバイアスで合計10となる
print(len(params))
# 上で書いた順番にパラメータが格納されている
# conv1の重みのサイズを確認する
print(params[0].size())
# conv2の重みのサイズを確認する
print(params[2].size())
10
torch.Size([6, 1, 5, 5])
torch.Size([16, 6, 5, 5])
ランダムな画像データ(32*32)を生成して、順伝播させる
# 入力データは畳み込み層に渡すために、4階のテンソル(サンプル数*チャネル数*縦の長さ*横の長さ)とする
input=Variable(t.randn(1,1,32,32))
# nn.Moduleクラスは、インスタンスに引数が渡された時にforwardメソッドを実行して戻り値を返す
# つまり、net(input)で順伝播の計算を行って結果を返す
out=net(input)
print(out)
Variable containing:
-0.0560 -0.0178 0.0846 -0.0223 -0.0512 -0.0304 -0.0159 -0.0462 0.0137 0.1008
[torch.FloatTensor of size 1x10]
勾配を0で初期化して、自動微分で出力に対する各パラメータの勾配を計算する
*勾配を0で初期化するのは、勾配がイテレーションごとに加算される仕様のため
net.zero_grad()
out.backward(t.randn(1, 10))
勾配が計算されていることを確認
params[0].grad.data
(0 ,0 ,.,.) =
0.0061 -0.0314 -0.0850 0.0349 -0.0878
0.0679 -0.0120 -0.0085 0.0657 0.0221
0.1048 -0.0141 -0.0240 0.0823 0.0642
0.0345 0.0288 -0.0962 0.0176 0.0349
-0.0347 -0.0072 0.0353 0.0261 -0.0101
(1 ,0 ,.,.) =
-0.0684 0.0127 0.0321 -0.0243 0.0584
0.0094 0.0007 -0.0568 0.0300 -0.0256
-0.0834 0.0171 0.0111 -0.0272 -0.0154
0.0159 -0.0254 0.0170 -0.0449 0.0476
-0.0106 0.0049 -0.0546 -0.0045 -0.0292
(2 ,0 ,.,.) =
-0.0322 -0.0255 0.0596 -0.0354 -0.0479
-0.0278 0.0321 -0.0208 0.0067 -0.0393
0.0173 -0.0347 0.0195 -0.0210 -0.0478
0.0678 0.0426 0.0089 0.0100 0.0728
0.0231 0.0130 0.0363 0.0550 0.0342
(3 ,0 ,.,.) =
-0.0236 0.0452 0.0599 -0.0137 0.0383
-0.0367 0.0237 0.0132 -0.0357 0.0477
-0.0280 0.0489 -0.0073 0.0253 -0.0305
0.0569 -0.0397 -0.0154 0.0011 0.0036
-0.0537 0.0570 0.0383 0.0062 0.0292
(4 ,0 ,.,.) =
-0.0364 -0.0462 0.0343 0.0040 -0.0054
-0.0533 -0.0116 -0.0613 -0.0817 -0.0258
0.0425 -0.0312 0.0581 0.0102 0.0594
0.0091 0.0295 -0.0293 0.0036 0.0140
0.0325 -0.0492 -0.0328 0.0752 -0.0051
(5 ,0 ,.,.) =
0.0459 0.0377 0.0353 -0.0119 -0.0537
-0.0074 -0.1080 -0.0230 0.0288 -0.0845
0.0033 -0.0077 -0.0215 -0.0441 -0.0072
-0.0434 0.0256 0.0534 -0.0232 0.0010
-0.0602 -0.0076 -0.0256 0.0523 -0.0060
[torch.FloatTensor of size 6x1x5x5]
Loss Function
損失関数を定義して計算する
# 出力
output=net(input)
# 教師データ(今回は適当に作成)
target=Variable(t.arange(1,11))
# 損失関数(平均二乗誤差)のインスタンスを生成
criterion=nn.MSELoss()
# 損失関数を計算
loss=criterion(output,target)
print(loss)
Variable containing:
38.4459
[torch.FloatTensor of size 1]
損失関数の計算グラフの一部を確認する
# MSELoss
print(loss.grad_fn)
# Linear
print(loss.grad_fn.next_functions[0][0])
# ReLU
print(loss.grad_fn.next_functions[0][0].next_functions[0][0])
<MseLossBackward object at 0x1247d9a58>
<AddmmBackward object at 0x1247d6cf8>
<ExpandBackward object at 0x124714668>
Backprop
自動微分で計算した勾配を使って、損失関数に対する各パラメータの勾配を計算する
# 勾配の初期化
net.zero_grad()
# conv1のバイアスを試しに確認する
# 計算前
print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)
# 勾配の計算
loss.backward()
# 計算後
print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)
conv1.bias.grad before backward
Variable containing:
0
0
0
0
0
0
[torch.FloatTensor of size 6]
conv1.bias.grad after backward
Variable containing:
1.00000e-02 *
7.4076
2.8857
5.5228
3.0977
5.4020
-1.6718
[torch.FloatTensor of size 6]
Update the weights
シンプルな勾配降下法で重みを更新する
learning_rate=0.01
# 学習した全てのパラメータについてforループで重みを更新する
for f in net.parameters():
#.sub_でlearning_rate*f.grad.dataを引き算してinplaceする
f.data.sub_(learning_rate*f.grad.data)
PyTorchの最適化モジュールを使う場合は以下のようになる
import torch.optim as optim
# SGDのインスタンスを生成
optimizer=optim.SGD(net.parameters(),lr=0.01)
# イテレーション毎に以下を実行する
# 勾配の初期化
optimizer.zero_grad()
# 出力の計算(順伝播)
output=net(input)
# 損失関数の計算
loss=criterion(output, target)
# 勾配の計算(誤差逆伝播)
loss.backward()
# 重みの更新
optimizer.step()