モンテカルロ法とは
モンテカルロ法(Monte Carlo Methods)とは、乱数を用いて積分計算やシミュレーションを行う手法のひとつで、CGの分野だと放射輝度を求める際に用いるレンダリング方程式の解法アルゴリズムとして主流となっています。
Buffonの針
モンテカルロ法を用いたシミュレーションの一例としてビュッフォン(Buffon)の針というものがあります。
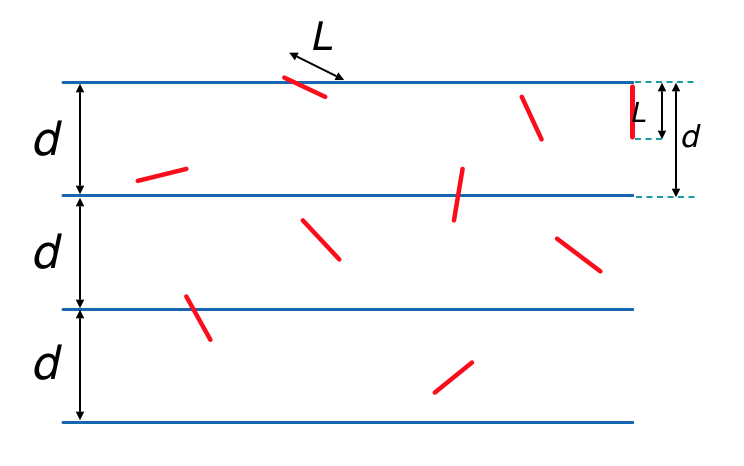
紙の上に等間隔に平行線を引き、その上にランダムに針を投げ 平行線と重なっている針の数を数えることで円周率の近似値を求める、という方法です。針と平行線が重なる確率を求めてみます。
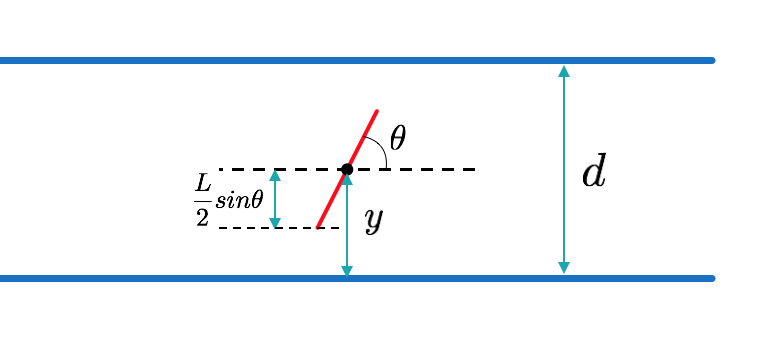
下図のように、平行線と針のなす角を$\theta$ $[0,\pi]$、
針の中心からもっとも近い平行線までの距離を$y$ $[0,\frac{d}{2}]$とします。
『針をランダムに投げる』ということは、この$\theta$と$y$を範囲内でランダムにとるということです。
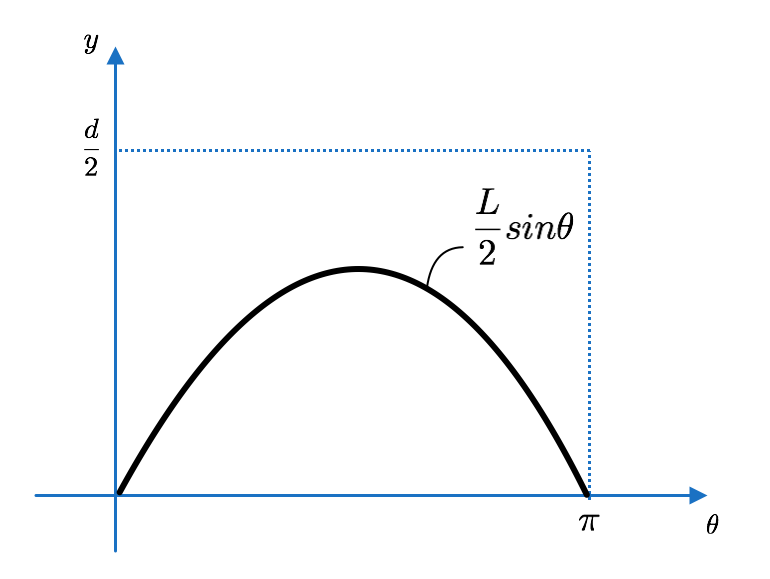
四角形の面積:${\pi d}/{2}$
グラフ下部分の面積:$\int ^{\pi }_{0}\frac {L}{2}\sin \theta d\theta =L$
より、求める確率は$$p=\dfrac {2L}{\pi d}$$となります。
ここで、式を簡単にするために平行線の間隔を $d=2L$ とすると
$$p=\frac {1}{\pi }$$となり、針と平行線が重なる確率と円周率$\pi$が逆数の関係にあることがわかります。
例えば、この実験を実際にやってみて針を5000本投げ、そのうち1593本が平行線と重なったとします。
すると求められる円周率の近似値は $$\pi\approx\frac{5000}{1593}=3.1387...$$ となります。
針を紙の上に投げるだけで円周率が求まるという原理もシンプルでわかりやすい方法ですが、人の手で何千本という針の数を数えるのにも限界があるため、サンプル数をあまり多くとることができません。
故に近似値の精度もあまり良いものではないですが、古くから記述が残されているモンテカルロ法による近似値計算の一例として紹介しました。
モンテカルロ積分
モンテカルロ推定関数
モンテカルロ法による定積分計算を考えてみます。
被積分関数を$f(x)$とし、定積分$$I=\int ^{b}_{a}f\left( x\right) dx$$を考えます。
この値をモンテカルロ法を用いて求める式はサンプル数$N$、確率密度関数$p(x)$とすると
$$\lt I \gt =\frac{1}{N}\sum^{N}_{i=1}\frac{f\left( x_{i}\right) }{p\left( x_{i}\right) }$$と定義され、この$\lt I \gt$をモンテカルロ推定関数(Estimator)といいます。
計算例
定積分$$I=\int ^{1}_{0}5x^4 dx$$を例としてモンテカルロ積分をやってみます。真値は1なので、1に近ければ近いほど良い結果(精度が良い)ということになります。
今回は$p(x)$として一様分布を用いています。
# モジュールのインポート
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return 5*x**4
def monte(N):
# 積分範囲[a,b]
a=0
b=1
# 範囲[a,b]での乱数をN個発生
x = (b-a)*np.random.rand(N)
ans = np.average(f(x))
return ans
被積分関数$f(x)$と積分範囲$[a,b]$でのモンテカルロ積分の値を返す関数monteを定義、引数$N$でサンプル個数を渡します。
サンプル個数100とすると
monte(100)
0.9481083397271469
と結果が返されます。サンプル数が100程度だとあまり良い結果は出ません。
ひとつだけやってみても結果の比較がやりづらいので、サンプル個数を変えながら結果を見てみましょう。
import pandas as pd
startx = 1
endx = 1000
interval = 1
sample = np.arange(startx,endx+startx,interval)
m_int = pd.DataFrame((np.random.randn(sample.size,2)+2)*0)
count = 0
for i in sample:
m_int[0][count] = i
m_int[1][count] = monte(i)
count += 1
m_int = m_int.rename( columns={0:'N',1:'ans'} )
m_int.plot( x='N', figsize=(13,8), title="y=5x^4")
plt.grid(which='major', color='black', linestyle='-')
plt.show()
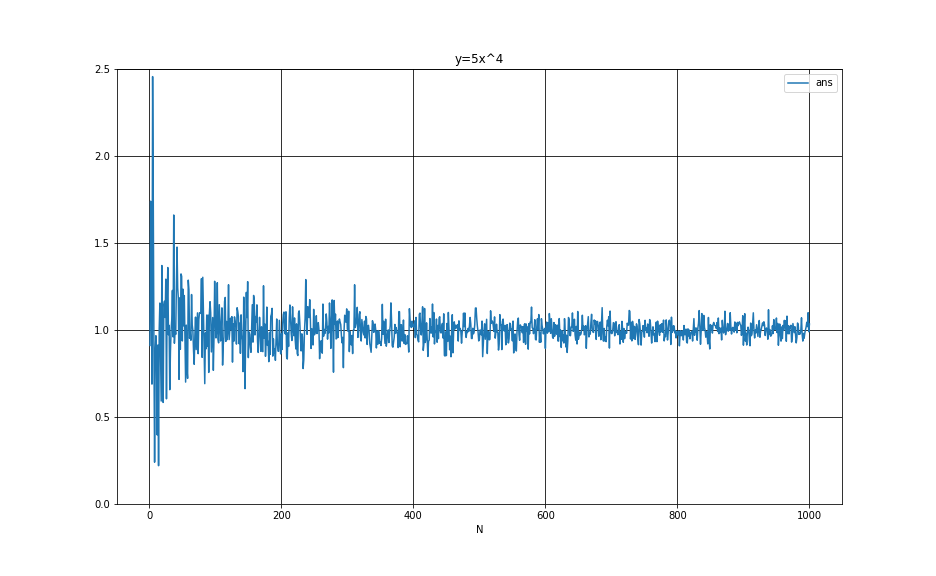
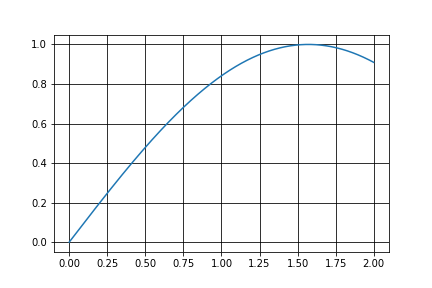
横軸はstartx~endxまでの範囲をinterval刻みでプロットしています。
今回はN=1からN=1000までの結果をグラフに表しました。サンプル数が増えるにつれて真値の1に近づいていることがわかります。
分散と標準偏差
先述の計算例でモンテカルロ法の特徴のひとつ、『サンプル個数が増えれば増えるほど精度が上がる』ということがわかりましたが、具体的にどのくらい精度が上がるのでしょうか?
ここである重み付け和$G(x)$を考えます。$$G(x)=\sum_{j=1}^{N}w_j g(x_j)$$先述の説明でいえば、$G(x)$はモンテカルロ推定関数、$g(x)$は被積分関数にあたります。
一様分布を用いた場合サンプル毎の重みは全て同じになり、$w_i=\frac{1}{N}$と書けるので
\begin{align}
G(x)=\sum_{j=1}^{N}\frac{1}{N} g(x_j)\\
=\frac{1}{N}\sum_{j=1}^{N} g(x_j)
\end{align}
と整理できます。この式は先述の計算例でのモンテカルロ推定関数と同じ式になります。
この関数の分散を考えると
\begin{align}
\sigma^2[G(x)]&=\sigma^2[\frac{1}{N}\sum_{j=1}^{N} g(x_j)] \\
&=\frac{1}{N^2}\sigma^2[\sum_{j=1}^{N} g(x_j)] \\
&=\frac{1}{N^2}N\sigma^2[g(x)] \\
&=\frac{1}{N}\sigma^2[g(x)]
\end{align}
となります。係数に$1/N$が出てきていることからわかるように、モンテカルロ推定関数の分散はサンプル数Nに反比例します。
分散がNに反比例するので、標準偏差は$\sqrt{N}$に反比例します。
つまり、誤差を半分にしたければサンプル数を4倍に、誤差を1/10倍にしたければサンプル数を100倍にする必要があるということです。
ここまでの計算からわかるように、モンテカルロ積分の真値への収束は非常に遅いです。この収束の遅さはモンテカルロ積分の問題点のひとつとなっており、さまざまな分散低減の手法が考えられています。
不偏と一致性
サンプル数を増やすことによってどのくらい誤差が小さくなっているのかを説明しました。現実的にはありえませんが、サンプル数を無限大とすれば誤差は0になり、モンテカルロ推定関数の値は完全に真値に一致します。
このような性質を一致性(Consistency)といい、この性質をもつ推定関数を一致推定量といいます。
また、推定関数の期待値が真値と一致するような性質を不偏(unbiased)といい、このような推定関数を不偏推定量といいます。逆にこのような性質を持たない推定関数は"偏りをもつ"関数といい、このような関数の期待値は真値に一致しません。
決定論的アルゴリズム vs モンテカルロ積分
モンテカルロ法の分散の低減が遅いということを述べましたが、次はモンテカルロ法を使うことのメリットについて説明します。
定積分の近似値を求める方法として他に挙げられるものに区分求積法や台形公式などがあります。
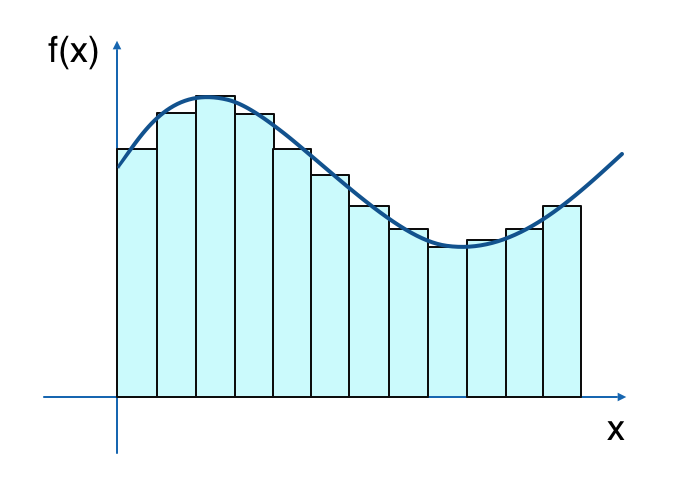
このような方法を決定論的アルゴリズムといいます。
さて、決定論的アルゴリズムである区分求積法で定積分を求めることを考えた場合、1次元積分で12個サンプル数をとると上図のような感じになります。
この図に奥行きが追加され2次元に拡張された図を想像してみると、サンプル数が12×12=144個になることがわかります。
さらに次元を上げていくと1728,20736...と、同じ精度を求めるためのサンプル数は爆発的に増加していき、
最終的に、d次元積分で各次元にN個サンプルをとった場合には$N^d$個のサンプル数が必要になってしまいます。
一方、モンテカルロ積分では次元数の増加によって必要なサンプル個数は左右されず、任意のサンプル数を選択することができます。本記事では説明のために1次元積分での例しか挙げていませんが、モンテカルロ積分が効果的に使えるのは高次元での積分問題だということです。
サンプリング手法
今までの説明では確率密度関数として一様分布を用いていたので、どの$x$をサンプルするかに偏りはなかったのですが、
時には一様ではなくある程度偏りのある確率分布を用いることで分散の低減が速くなる場合があります。
本章ではそのようなサンプリング手法の一例を紹介します。
逆関数法
逆関数法とは、[0,1]上で発生させた一様乱数を用いて任意の確率分布関数$f(x)$の累積密度関数$F(x)$に従う乱数を生成する手法です。
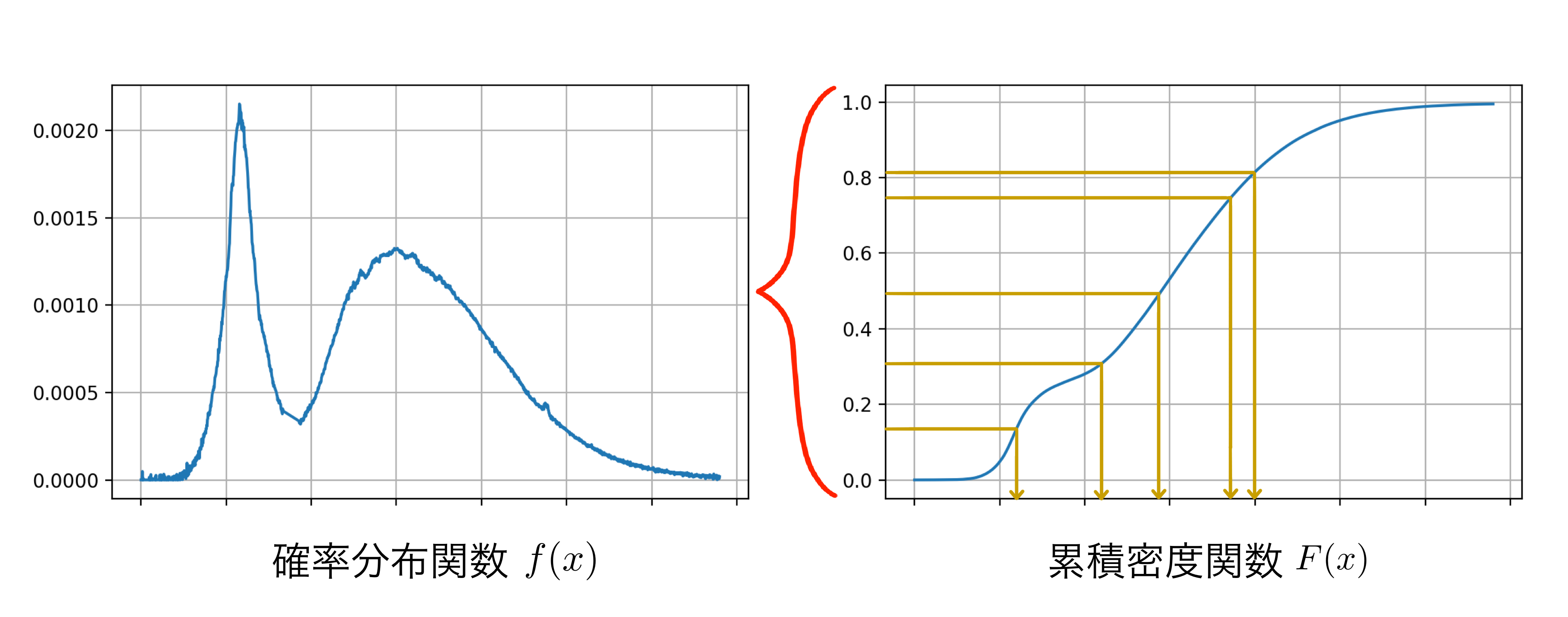
累積密度関数はその部分までの値をとる確率をプロットしたものなので、値は0から1までです。図で説明すると$F(x)$の縦軸から一様に値を発生させ、$F^{-1}(x)$を算出して新たな乱数として扱う、といった感じです。
$F(x)$は$f(x)$を積分した関数なので、$f(x)$で値が比較的大きい部分は$F(x)$での勾配が急になっている部分にあたります。図からわかるようにこの部分は縦軸から一様に値を選ぶとサンプルされやすい部分となっており、多くのサンプルが集まる部分といえます。
任意の関数の分布にしたがう乱数を発生させることができますが、累積密度関数$F(x)$の逆関数$F^{-1}(x)$を求める必要があり、解析的にこの関数が求まる場合には有効ですが、複雑すぎる関数の場合には使いづらい手法となっています。
棄却サンプリング
棄却サンプリングとは、[0,1]上で発生させた乱数を用いて任意の確率分布関数$f(x)$に従う乱数を生成する手法です。
$u_i$を[0,1]上で発生させた乱数、(今回は一様乱数とします)
$x$を[a,b]上で発生させた乱数、
$M$をすべての$x$で $Mp(x)>f(x_i)$ を満たす定数とすると、$$u_i<\frac{f(x_i)}{M}$$この不等式を満たす$x_i$を採択、満たさない$x_i$を棄却します。
言葉や式だけで説明してもよくわからないので、図を描いてみます。
まず、"$M$をすべての$x$で $Mp(x)>f(x_i)$ を満たす定数とする"ということは、
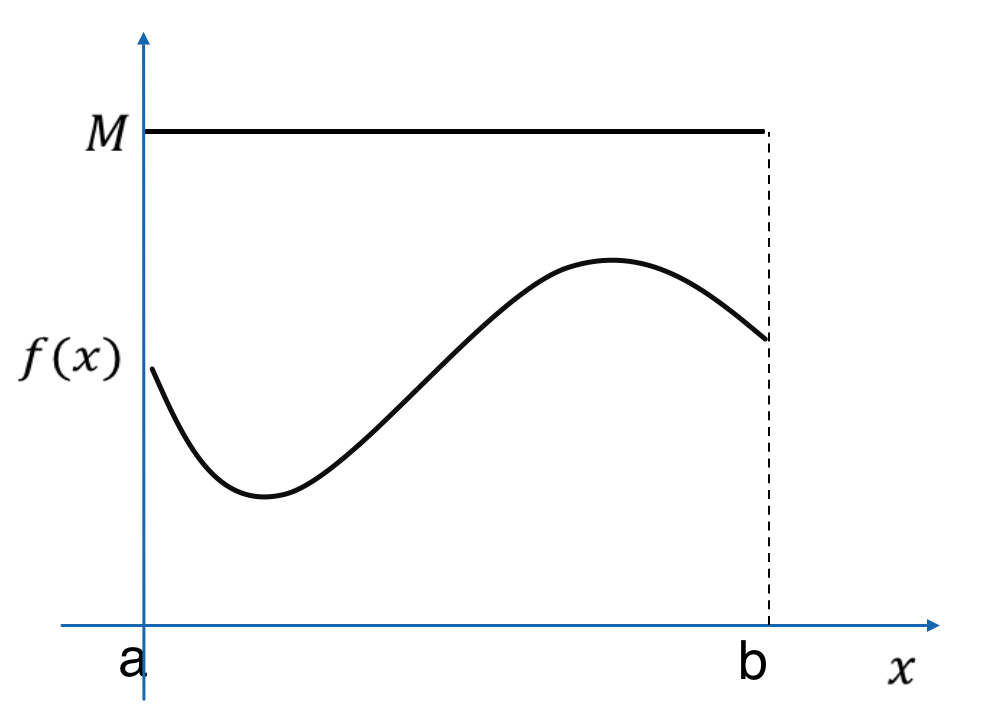
上図のように、$p(x)$を定数倍して$f(x)$を覆うような状態になっていればよい、ということです。
次に、今回は乱数を2種類使用しているので、$u$と$x$を発生させるということは
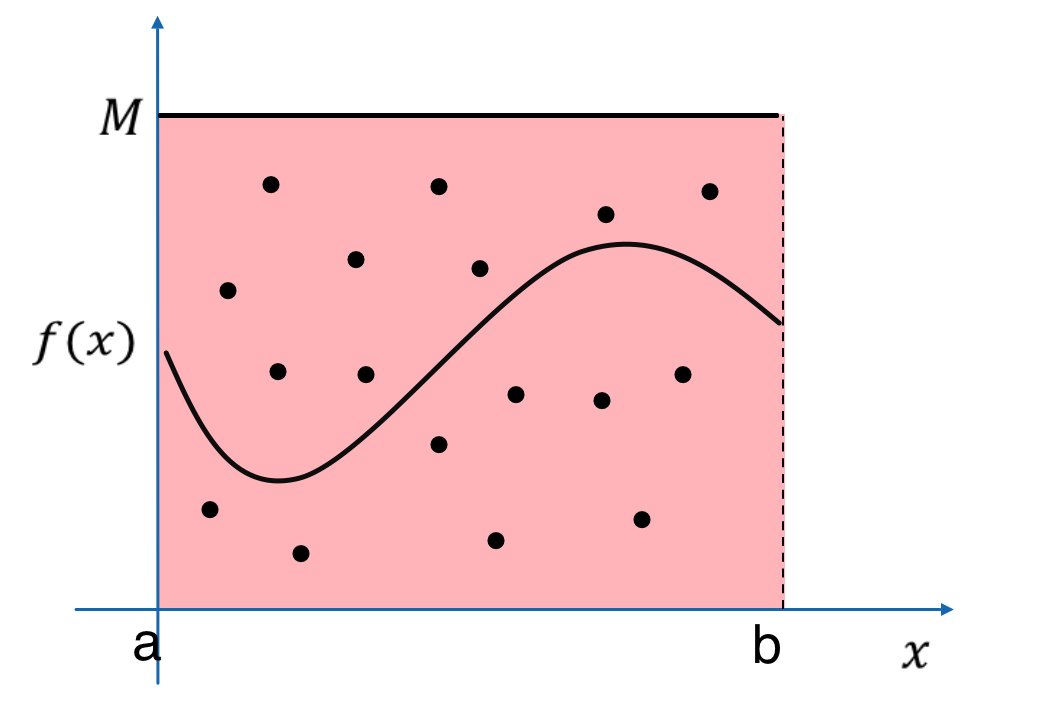
上図のように、$[0,M]×[a,b]$の範囲内でランダムに点をプロットすることと同義です。
最後に不等式を満たすような点ですが、これは
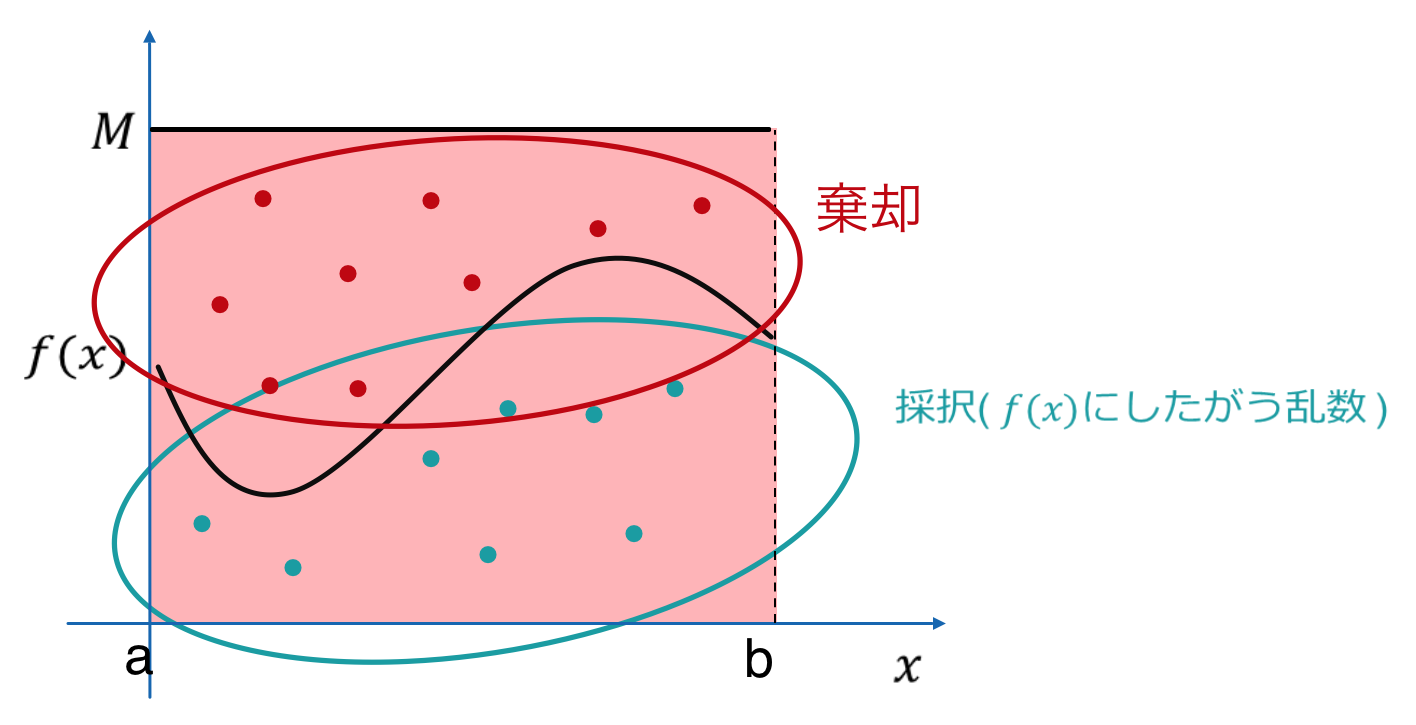
グラフより下部にある点は採択、上部にある点は棄却するということになります。
以上のアルゴリズムで$f(x)$にしたがうサンプルを生成することができます。
計算例
今回は範囲[0,2]で関数$$f(x)=sinx$$にしたがうサンプルを生成してみます。
def f(x):
return np.sin(x)
# 積分範囲[a,b],定数M
a=0
b=2
M=2
def rejection_sampling(N):
sum = 0
count = 0
x = (b-a)*np.random.rand(N)
u = np.random.rand(N)
accept_x = (-1)*np.ones(N)
for i in range(N):
if M*u[i] < f(x)[i]:
accept_x[i] = x[i]
return accept_x
関数$f(x)$、サンプル数Nを引数として渡し採択したサンプルを返す関数regection_samplingを定義。
accept_xの棄却された部分には値-1が入っています。
定数$M$は$f(x)$を覆っていればなんでも良いので、今回はM=2としています。
$f(x)$はこんな感じのグラフ。
# f(x)描画
x = np.arange(a,b,0.001)
plt.plot(x,f(x))
plt.grid(which='major', color='black', linestyle='-')
plt.show()
# サンプル生成
N=10000
result = rejection_sampling(N)
# f(x)描画
x = np.arange(a,b,0.01)
plt.plot(x,(N/200)*f(x))
# ヒストグラム描画
plt.hist(result, bins=100, range=(a,b))
plt.grid(which='major', color='black', linestyle='-')
plt.show()
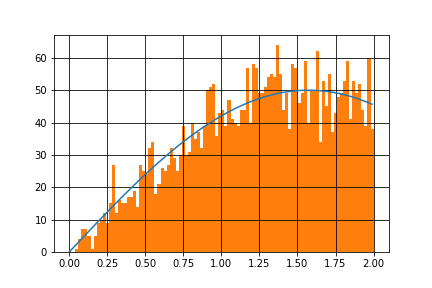
N=10000の場合です。サインカーブにしたがうサンプルが生成されていることがわかります。
さて、この棄却サンプリングですが、あまり有効でない場合があります。
それは"採択されるサンプル数が少なくなる場合"です。
このような例のひとつとして、関数$$f(x)=x^{20}$$にしたがうサンプルを生成してみましょう。
グラフを描画してみます。
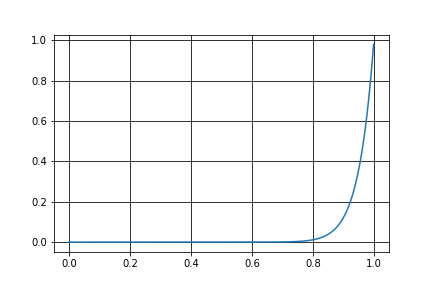
このグラフを見てわかる通り、前章で述べた不等式を満たす領域が小さいことがわかります。
def f(x):
return x**20
前述のコードの$f(x)$部分を書き換えて実行します。
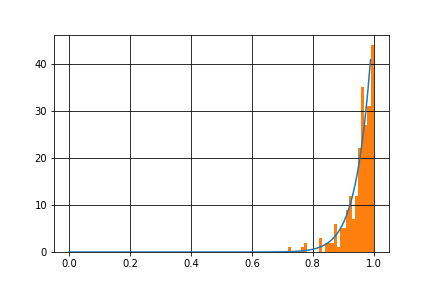
$f(x)$にしたがうサンプルは生成できていますが、これでは生成されたサンプルの個数自体が少なくなってしまうので、近似の精度の低下を招きます。
棄却サンプリングを使う際はできるだけ採択されるサンプルが多くなるような関数$f(x)$、定数$M$を選択すべきでしょう。
層化サンプリング
ある範囲内でのサンプリングの集中によって、モンテカルロ積分を計算する際に寄与の小さい部分を集中的に加算し、分散が大きくなってしまうことがあります。
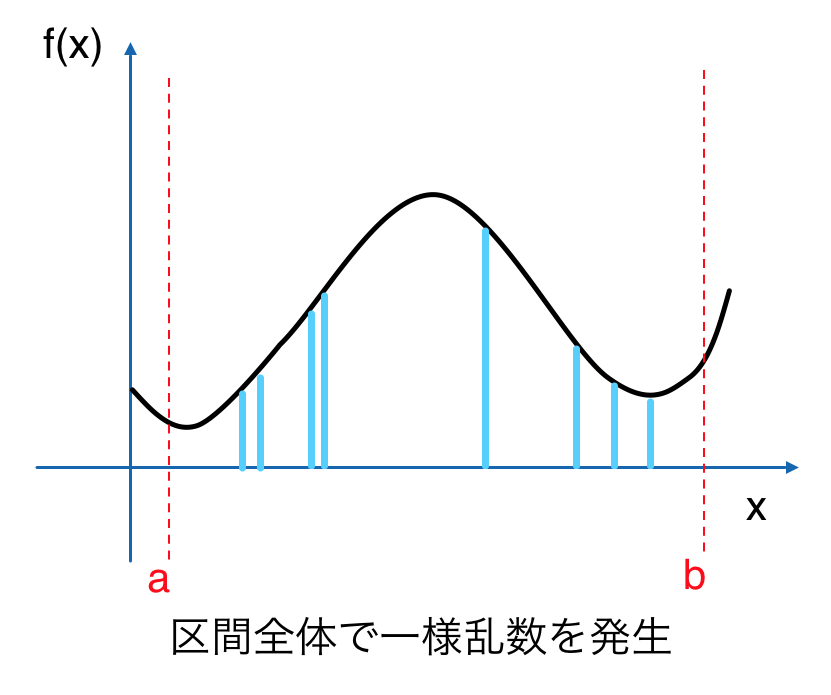
**層化サンプリング(stratified sampling)**を用いることでこのような状況を防ぐことができます。
層化サンプリングのアルゴリズムは単純で、サンプルをとる範囲内で小区間に分け、その区間毎にサンプルをとるというものです。
ちなみにこの分けられた小区間のことをstrataというらしいです。
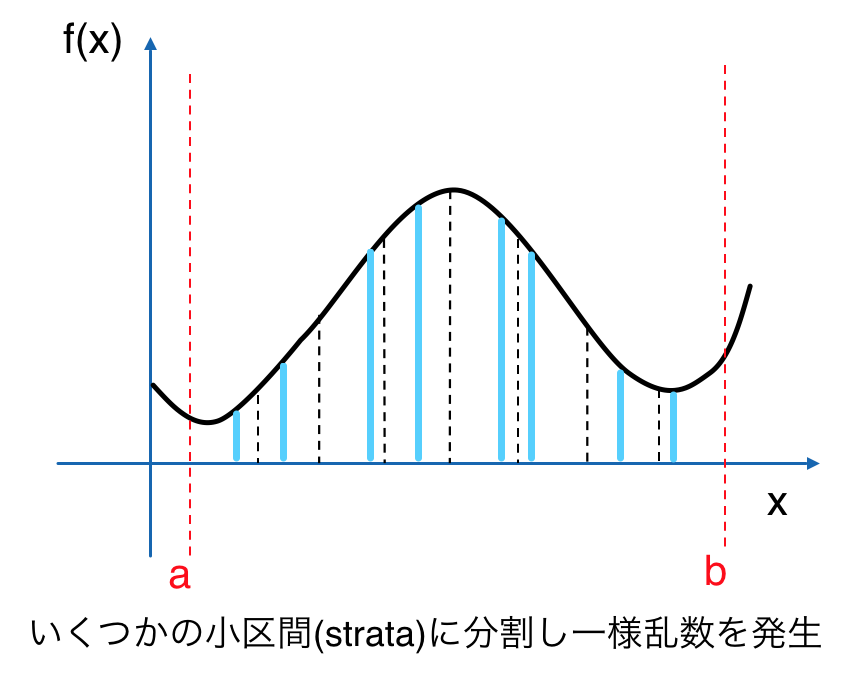
普通に範囲内で一様にサンプリングした場合との分散の比較を考えてみます。
まず、層化サンプリングでの分散の式は
\sigma^2=\sum_{j=1}^{m}\frac{\alpha_j-\alpha_{j-1}}{n_j}\int_{\alpha_{j-1}}^{\alpha_j}f(x)^2dx
-\sum_{j=1}^{m}\frac{1}{n_j}\bigl(\int_{\alpha_{j-1}}^{\alpha_j}f(x)dx\bigr)^2
と表せます。
$\alpha_j-\alpha_{j-1}$は$j$番目の小区間の範囲、$n_j$は小区間ひとつごとのサンプル個数を表すパラメータです。
上図で示した通り、全ての小区間の範囲が等しく、区間毎のサンプル数が1つの場合を考えます。
また、式を簡潔にするために範囲を[0,1]とします。
範囲内を小区間$m$個に分けるので$$\alpha_j-\alpha_{j-1}=\frac{1}{m}$$また、区間毎のサンプル個数は1なので$$n_i=1$$と表せます。この2つの式を代入して整理すると、分散は
\begin{align}
\sigma^2&=\sum_{j=1}^{m}\frac{\alpha_j-\alpha_{j-1}}{n_j}\int_{\alpha_{j-1}}^{\alpha_j}f(x)^2dx
-\sum_{j=1}^{m}\frac{1}{n_j}\bigl(\int_{\alpha_{j-1}}^{\alpha_j}f(x)dx\bigr)^2 \\
&=\sum_{j=1}^{m}\frac{1}{m}\int_{\alpha_{j-1}}^{\alpha_j}f(x)^2dx
-\sum_{j=1}^{m}\bigl(\int_{\alpha_{j-1}}^{\alpha_j}f(x)dx\bigr)^2 \\
&=\frac{1}{m}\sum_{j=1}^{m}\int_{\alpha_{j-1}}^{\alpha_j}f(x)^2dx
-\sum_{j=1}^{m}\bigl(\int_{\alpha_{j-1}}^{\alpha_j}f(x)dx\bigr)^2
\end{align}
と導出できます。
一方、純粋なモンテカルロ法での分散を求めてみます。
純粋なモンテカルロ法は、区間数を1、区間毎でのサンプル個数をNとしたものと考えることができるので
\begin{align}
\alpha_j-\alpha_{j-1}&=1 \\
n_j&=N
\end{align}
とパラメータを設定でき、前述の分散の式に代入して整理すると
\begin{align}
\sigma^2&=\sum_{j=1}^{m}\frac{\alpha_j-\alpha_{j-1}}{n_j}\int_{\alpha_{j-1}}^{\alpha_j}f(x)^2dx
-\sum_{j=1}^{m}\frac{1}{n_j}\bigl(\int_{\alpha_{j-1}}^{\alpha_j}f(x)dx\bigr)^2 \\
&=\sum_{j=1}^{m}\frac{1}{N}\int_{\alpha_{j-1}}^{\alpha_j}f(x)^2dx
-\sum_{j=1}^{m}\frac{1}{N}\bigl(\int_{\alpha_{j-1}}^{\alpha_j}f(x)dx\bigr)^2 \\
&=\frac{1}{N}\sum_{j=1}^{m}\int_{\alpha_{j-1}}^{\alpha_j}f(x)^2dx
-\frac{1}{N}\sum_{j=1}^{m}\bigl(\int_{\alpha_{j-1}}^{\alpha_j}f(x)dx\bigr)^2
\end{align}
となります。ここで2式の第2項に着目すると、層化サンプリングの分散の式では係数が1、純粋なモンテカルロ法での分散の式では係数が$1/N$となっていることがわかります。
係数のかけられている被積分関数での各区間ごとの積分値の2乗の和は必ず正の値になるので、層化サンプリングでの分散が純粋なモンテカルロ法での分散よりも小さくなっていることがわかります。
次に、区間毎に2つずつサンプリングした場合の分散を考えてみます。
\begin{align}
\alpha_j-\alpha_{j-1}&=\frac{2}{m} \\
n_j&=2
\end{align}
条件に応じ、以上の式を代入して分散を計算します。
\begin{align}
\sigma^2&=\sum_{j=1}^{m}\frac{\alpha_j-\alpha_{j-1}}{n_j}\int_{\alpha_{j-1}}^{\alpha_j}f(x)^2dx
-\sum_{j=1}^{m}\frac{1}{n_j}\bigl(\int_{\alpha_{j-1}}^{\alpha_j}f(x)dx\bigr)^2 \\
&=\sum_{j=1}^{m}\frac{2}{m}\frac{1}{2}\int_{\alpha_{j-1}}^{\alpha_j}f(x)^2dx
-\sum_{j=1}^{m}\frac{1}{2}\bigl(\int_{\alpha_{j-1}}^{\alpha_j}f(x)dx\bigr)^2 \\
&=\frac{1}{m}\sum_{j=1}^{m}\int_{\alpha_{j-1}}^{\alpha_j}f(x)^2dx
-\frac{1}{2}\sum_{j=1}^{m}\bigl(\int_{\alpha_{j-1}}^{\alpha_j}f(x)dx\bigr)^2
\end{align}
この値と区間毎に1つずつサンプリングした場合の分散を比較すると、第2項の係数が小さくなっているので
分散が大きくなっていることがわかります。
つまり、層化サンプリングを行う時は区間毎のサンプル数は1つにすることで分散が最も小さくなるということです。
重点的サンプリング
本記事の前半で、モンテカルロ推定関数というものを定義しました。
\lt I \gt =\frac{1}{N}\sum^{N}_{i=1}\frac{f\left( x_{i}\right) }{p\left( x_{i}\right) }
モンテカルロ積分の計算例では確率分布として一様分布を用いて説明しましたが、被積分関数$f(x)$に応じた確率分布を用いることで分散の低減を早めることができます。
この任意の確率密度関数$p(x)$を用いたサンプリング手法を**重点的サンプリング(importance sampling)**といいます。
任意の$p(x)$と言いましたが、具体的にどんな関数が収束を速めやすいのかを考えてみます。
重点的サンプリングの分散の式を$p$の関数$L(p)$として表すと
\begin{align}
L(p)&=\int_{D}\biggl(\frac{f(x)}{p(x)}\biggr)^2 p(x)dx+\lambda\int_{D} p(x) dx \\
&=\int_{D}\biggl(\frac{f(x)^2}{p(x)}+\lambda p(x)\biggr) dx
\end{align}
となります。境界条件 $\int_{D} p(x) dx=1$ のもとで$L(p)$を最小化する$p(x)$は
\begin{align}
p(x)=\frac{1}{\sqrt{\lambda}}f(x)
\end{align}
と求まります。係数$1/\sqrt{\lambda}$は定数なので、被積分関数$f(x)$に比例するような確率分布を用いれば分散が最小(0)になることがわかります。
しかし、この係数の分母は$f(x)$の積分範囲での定積分の値になります。
そもそも求めたい定積分の値がわかっていなければこのような$p(x)$は求めることができないので、実質分散を0にする$p(x)$は求められないと考えていいでしょう。
分散を0にする確率密度関数は求められませんが、この結果から分散を小さくする$p(x)$はできるだけ被積分関数に比例した関数だということがわかります。
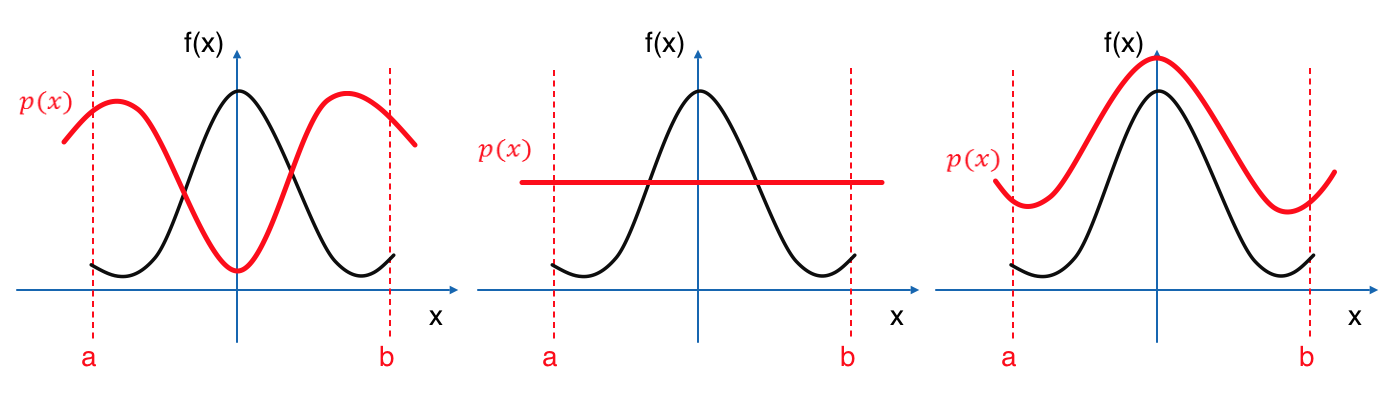
直感的にも、面積を計算する際に$f(x)$の値が大きい部分は寄与が大きくなるので
この部分でサンプルを多くとれるような確率密度関数を用いると、少ないサンプル個数でも良い結果となることがわかると思います。(上図右)
逆に、被積分関数にまったく比例しない(形が違う)$p(x)$を用いると、一様分布の場合と同じサンプル個数でも
分散が大きくなり、あまり良い結果は得られないでしょう。(上図左)
参考文献
Advanced Global Illumination[2006]
by Philip Dutre, Philippe Bekaert, Kavita Bala