皆さんこんにちは。今日も引き続きChatGPT先生をお迎えして、「ChatGPTとPythonで学ぶ 線形判別分析」というテーマで雑談したいと思います。それではChatGPT先生、よろしくお願いします。
assistant:
いつもありがとうございます。今日は、線形判別分析(Linear Discriminant Analysis/ LDA)についてお話します。
線形判別分析は、適用データの分布を最適に判別し、予測のために統計機能に基づいて適用データを最適な次元へ射影するという目的を持った技術です。主に次元削減の手法として使われますが、線形分類機としても使えます。
Pythonでは、線形判別分析を行うためのライブラリとして、Scikit-learnがあります。具体的にコードを見ながら、どのように使うか学びましょう。
user:
それでは、線形判別分析について学ぶためのPythonコードと、その説明を日本語で詳しく書いてください。結果の可視化もお願いします。
assistant:
もちろんです。まずは必要なライブラリをインポートします。
import numpy as np
from sklearn import datasets
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
import matplotlib.pyplot as plt
次にデータをロードします。ここでは、sklearnの付属のデータセット、wineを使います。
wine = datasets.load_wine()
X = wine.data
y = wine.target
ここでXは特徴ベクトル(データセットのラベルなしの部分)、yは対応するラベル(正解ラベル)です。
そして、線形判別分析のインスタンスを作成します。ここで注意するべきは、変換後の次元数を指定する点です。以下みたいにします。
lda = LinearDiscriminantAnalysis(n_components=2)
ここでn_components=2とすることで、データを2次元に削減することを示しています。
次に、フィットさせながら変換も同時に行います:
X_lda = lda.fit_transform(X, y)
最後に、結果をプロットします:
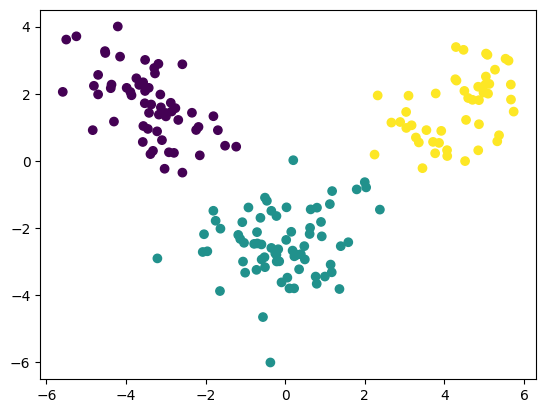
plt.scatter(X_lda[:, 0], X_lda[:, 1], c=y)
plt.show()
以上が線形判別分析を実施する一連の流れです。特徴ベクトルが高次元だったとしても、指定した次元数に縮約した形でプロットすることができます。この結果は特に散布図(scatter plot)として描かれます。
これを見ることで、データを2次元に縮小した際に、どの程度クラスごとに分けることが可能かを観察することができます。異なるクラス(色やマーカーで示される)がよく分けられていれば、LDAがよく機能しているということができます。
user:
同じデータに対して、線形判別分析による結果と、主成分分析による結果を可視化して比較するコードを書いてください。
assistant:
もちろんです。以下にコードを提供します。
まずは必要なライブラリをインポートします。
from sklearn.decomposition import PCA
見やすくするために、プロット用の関数を定義しておきましょう。
def plot_scatter(X, y, title):
plt.scatter(X[:, 0], X[:, 1], c=y)
plt.title(title)
plt.show()
次に、PCAとLDAを同様の方法で適用します。
# LDA
lda = LinearDiscriminantAnalysis(n_components=2)
X_lda = lda.fit_transform(X, y)
# PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
# プロット
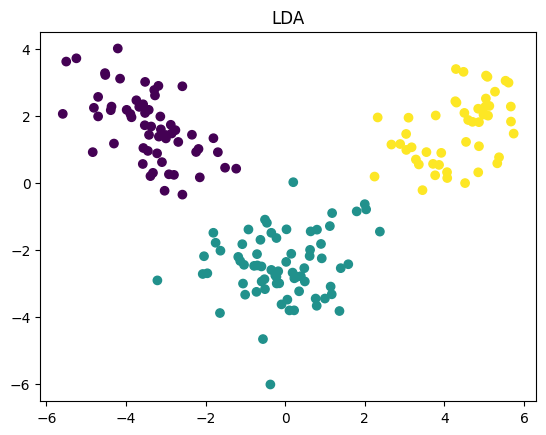
plot_scatter(X_lda, y, title='LDA')
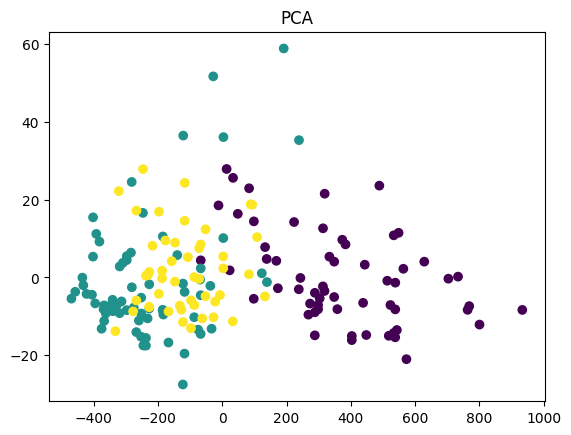
plot_scatter(X_pca, y, title='PCA')
これによりPCAとLDAの結果を比較することが可能です。LDAはクラスの分離を最適化しますので、クラスが重なっている場合はLDAの方が優れた結果を提供することが多いです。しかしPCAは全体的なデータのバリエーションを可能な限り保持しようとしますので、特定のクラスだけに偏らず、全てのデータをバランスよく表現しようと試みます。結果的に選択は問題やデータに依存します。
user:
同じデータを正規化したものに対して、線形判別分析による結果と、主成分分析による結果を可視化して比較するコードを書いてください。
assistant:
sklearnには、データを正規化するためのStandardScalerという便利な機能があります。この機能を使うと、各特徴量の平均が0、標準偏差が1になるようにデータをスケーリングすることができます。以下がそのコードです。
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
# データの正規化
X_norm = sc.fit_transform(X)
# 正規化したデータに対するLDAとPCAの適用
X_norm_lda = lda.fit_transform(X_norm, y)
X_norm_pca = pca.fit_transform(X_norm)
# 結果のプロット
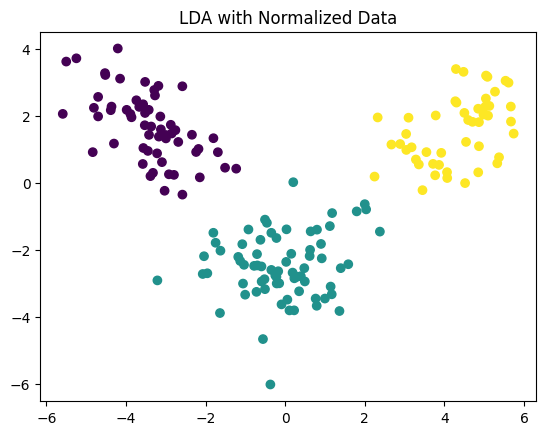
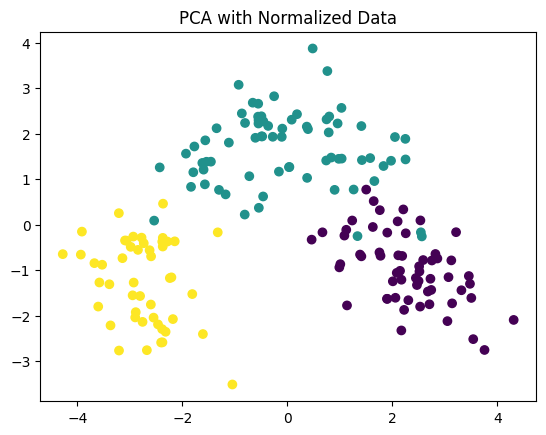
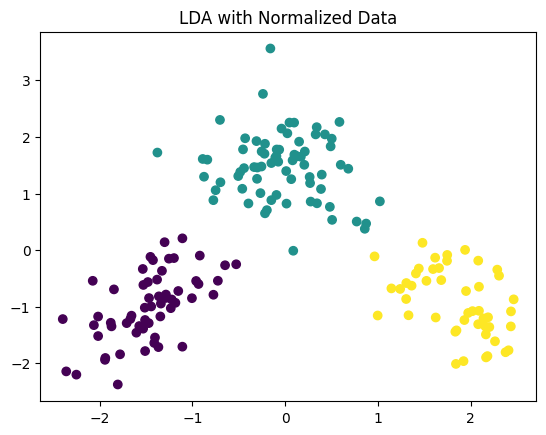
plot_scatter(X_norm_lda, y, title='LDA with Normalized Data')
plot_scatter(X_norm_pca, y, title='PCA with Normalized Data')
正規化(標準化)は各特徴が同じスケールになるように変換します。これにより、特徴間のスケールが大きく異なる場合にPCAやLDAの結果が偏ることを防ぎます。したがって、特徴のスケーリングが問題になる場合(例えば、一部の特徴が他の特徴と比べて非常に大きな値をとる場合など)は、データを正規化してからPCAやLDAを適用することを推奨します。
user:
線形判別分析をより深く学ぶために、sklearn.discriminant_analysis の LinearDiscriminantAnalysis を使わずにスクラッチで線形判別分析を行なうコードを実装し、同じデータに対して実行して結果を可視化してください。
assistant:
線形判別分析(LDA)をスクラッチで行うためには、以下の手順を実装します。
- 各クラスの平均ベクトルを計算
- クラス間変動行列(Between class scatter)とクラス内変動行列(Within class scatter)を計算
- これらの変動行列から線形判別ベクトルを得るために、固有値問題を解く
- 大きな固有値を持つ固有ベクトル(線形判別ベクトル)を選択
以下に、これらの手順を全て含んでいるコードを提供します。
class LDA:
def __init__(self, n_components):
self.n_components = n_components
self.linear_discriminants = None
def fit(self, X, y):
height, width = X.shape
class_labels = np.unique(y)
# Within class scatter matrix
mean_overall = np.mean(X, axis=0)
SW = np.zeros((width, width))
for c in class_labels:
_X = X[y == c]
_mean = np.mean(_X, axis=0)
SW += (_X - _mean).T @ (_X - _mean)
# Between class scatter matrix
SB = np.zeros((width, width))
for c in class_labels:
_X = X[y == c]
_mean = np.mean(_X, axis=0)
_N = _X.shape[0] # データの個数
SB += _N * (_mean - mean_overall).reshape(-1, 1) @ (_mean - mean_overall).reshape(1, -1)
# Linear discriminants
eigvals, eigvecs = np.linalg.eig(np.linalg.pinv(SW) @ SB)
eigvecs = eigvecs.T
idxs = np.argsort(abs(eigvals))[::-1]
eigvals = eigvals[idxs]
eigvecs = eigvecs[idxs]
self.linear_discriminants = eigvecs[0:self.n_components]
def transform(self, X):
return np.real(X @ self.linear_discriminants.T)
# 標準化したデータに対してLDA
lda = LDA(n_components=2)
lda.fit(X_norm, y)
X_lda = lda.transform(X_norm)
# 結果のプロット
plot_scatter(X_lda, y, title='LDA with Normalized Data')
scikit-learnのLinearDiscriminantAnalysisとは結果が少しひと異なることがあります。それは、scikit-learnではシュウィンクの修正(shrinkage)と呼ばれる正則化がデフォルトで適用されているためです。しかし、基本的なアイデアは上記のコードと同じです。
user:
ありがとうございます。上記のスクラッチ実装と、scikit-learnの実装とで、異なる部分についてもっと詳しく教えてください。
assistant:
線形判別分析の基本的なアイディアは、クラスの平均間の距離を最大化し、クラス内のスキャッタ(散らばり具合)を最小化することにあります。そのため基本的には、上記のスクラッチ実装とscikit-learnのLinearDiscriminantAnalysisで同じことを行っています。スクラッチの実装は理解のための単純な実装で、scikit-learnのLinearDiscriminantAnalysisはより高度な利用者向けに設計されています。
scikit-learnのLinearDiscriminantAnalysisは様々なパラメータを調整してモデルを最適化でき、これらパラメータは上記のスクラッチ実装では対応していません。特に、shrinkageパラメータは正則化項を導入し、solverパラメータをlsqrまたはeigenに設定することでクラス内変動行列の最適な逆行列を求めることができます。
また、scikit-learnの実装では計算が最適化されていて大規模データにも対応できるようになっています。
そのため、理解のためにスクラッチで実装することは大切ですが、実際の問題解決にはscikit-learnのようなライブラリを使用することを推奨します。これらのパッケージは頑健性と効率性を追求しており、数値的安定性やエラーハンドリングのような細かい点が処理されています。
user:
ありがとうございます。sklearn.discriminant_analysis には QuadraticDiscriminantAnalysis というものもあるのですが、これについても詳しく教えてください。
assistant:
はい、確かにsklearn.discriminant_analysisモジュールにはQuadraticDiscriminantAnalysis(QDA)というクラスも存在します。これはLDAと同様に、特徴空間内でクラスを分離するための線形判別分析を実行しますが、QDAはクラス分離においてクラスごとに異なる共分散行列を考慮します。
具体的に言うと、LDAはデータが各クラス内で同じ共分散を共有するという仮定に基づいています。これにより線形の決定境界を得ます。一方で、QDAは各クラスが自身の共分散行列を持つというより一般的な仮定に基づいています。そのためクラス間の決定境界は二次的(曲線的)になります。
QDAはLDAより柔軟なモデルを提供しますが、データ点ごとに共分散を推定するためのパラメータが多くなるため、大きなデータセットが必要となるというトレードオフがあります。
以下にQDAを使用する簡単な例を示します:
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
qda = QuadraticDiscriminantAnalysis()
qda.fit(X_train, y_train)
predictions = qda.predict(X_test)
ここで、X_trainとy_trainは訓練データ、X_testはテストデータになります。このコードはQDAモデルを訓練データにフィットさせ、その後でテストデータを使って予測を行います。その予測結果はpredictionsに格納されます。
user:
同じデータに対して、線形判別分析と二次判別分析を行い、結果を可視化して比較するコードを書いてください。
assistant:
はい、それは可能です。以下にそれぞれの判別分析を行うコードと、その後のプロットを示します。
まずは必要なライブラリをインポートします。
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
次に、LDAとQDAを一般的な方法で設定し、フィットして予測を行います。
# LDA の実施
lda = LinearDiscriminantAnalysis(n_components=2)
X_lda = lda.fit_transform(X, y)
# QDA の実施
qda = QuadraticDiscriminantAnalysis()
qda.fit(X,y)
X_qda = qda.predict_proba(X)
# プロット
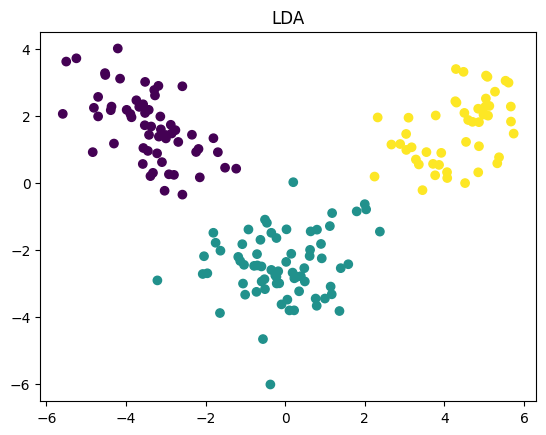
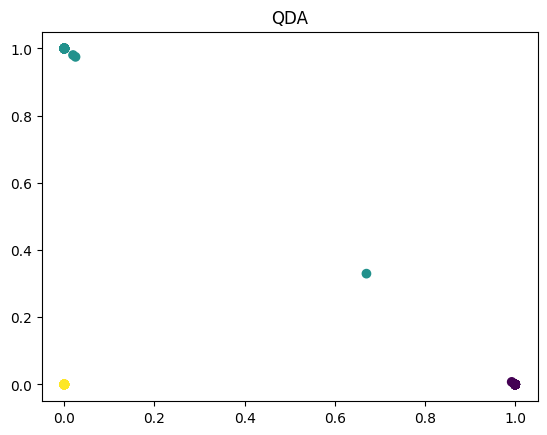
plot_scatter(X_lda, y, title='LDA')
plot_scatter(X_qda, y, title='QDA')
このコードは主にLDAとQDAの比較を行います。LDAは線形な決定境界を提供し、QDAはより柔軟な二次の決定境界を提供します。
しかし、注意点として、QDAのpredict_probaメソッドは予測確率を返します。これはベクトルが各クラスに所属する確率を意味し、クラスラベルそのものを予測するわけではありません。そのため、上記のスクリプトのplot_scatter関数はQDAの結果を正確に表示しないかもしれません。完全な対応のためにはpredict_probaの結果を別の方法で可視化する必要があります。この点は、確認してみてください。
user:
QDAでfit_transformを使わない理由がよくわからないのですが、どういう理由でしょうか?
assistant:
QuadraticDiscriminantAnalysisクラスにはfit_transformメソッドが含まれていません。これは、QDAが本来は次元削減のために使われるものではなく、クラスの確率モデルを学習し、新たな観測値がどのクラスに所属するかを予測するカテゴリカルな問題に特化したものだからです。
一方で、主成分分析(PCA)や線形判別分析(LDA)は次元削減のための手法であり、特徴量の次元を減らすために使われます。そのため、これらにはfit_transformメソッドがあり、訓練データを引数に取り、次元削減を行った結果を返します。
QDAでは、訓練データに対してfitメソッドを用いてモデルを学習し、その後で新たなデータに対してpredictまたはpredict_probaメソッドを用いて各クラスに所属する確率を予測します。
したがって、QDAを使ってデータの次元削減を行いたいときには、他の方法を考える必要があります。例えば、QDAの結果(各クラスへの所属確率)をそのままプロットする、または一部の結果だけをプロットするなどです。ただし、これらの方法でプロットした結果が直感的に理解しやすいわけではないことは注意が必要です。
user:
二次判別分析をより深く学ぶために、sklearn.discriminant_analysis の QuadraticDiscriminantAnalysis を使わずにスクラッチで二次判別分析を行なうコードを実装し、同じデータに対して実行して結果を可視化してください。
assistant:
QuadraticDiscriminantAnalysis (QDA)をスクラッチで実装するためには、クラスごとに共分散行列を推定し、これを用いて各クラスの確率密度関数を計算する必要があります。以下に、2つのクラスを持つデータに対してQDAを行う簡易的なスクラッチ実装を示します。
import numpy as np
from scipy.stats import multivariate_normal
class QDA:
def fit(self, X, y):
self.classes = np.unique(y)
self.params = {}
for c in self.classes:
X_c = X[y == c]
self.params[c] = {
'mean': X_c.mean(axis=0),
'cov': np.cov(X_c.T),
'prior': X_c.shape[0] / X.shape[0]
}
def predict(self, X):
posteriors = []
for c in self.classes:
prior = self.params[c]['prior']
likelihood = multivariate_normal.pdf(X, mean=self.params[c]['mean'], cov=self.params[c]['cov'])
posteriors.append(prior * likelihood)
return self.classes[np.argmax(posteriors, axis=0)]
# データの準備
from sklearn.datasets import make_classification
from sklearn.preprocessing import StandardScaler
X, y = make_classification(n_samples=300, n_features=2, n_informative=2, n_redundant=0, n_classes=2, random_state=42)
sc = StandardScaler()
X = sc.fit_transform(X)
# QDA の実施
qda = QDA()
qda.fit(X, y)
y_qda = qda.predict(X)
# プロット
plt.scatter(X[:, 0], X[:, 1], c=y_qda)
plt.title('QDA')
plt.show()
このコードでは、入力データXとクラスラベルyからクラスの平均と共分散行列を学習し、推定するfitメソッドと、学習したパラメータを用いて新しいデータXのクラスラベルを予測するpredictメソッドを定義しています。
この結果からわかるように、QDAは非線形な決定境界(訓練データを元にした色分け)を生成します。
ただし、このコードは二項分類に対してのみ機能し、また多項分類に拡張するには色々な技巧が必要となります。また、共分散行列がシンギュラー(逆行列が存在しない)になるなどの問題を解決するための補正が全く行われていません。そのため、実運用にはScikit-learnなどの既存のライブラリを使うことを強く推奨します。
user:
線形判別分析は、判別能力が低かったとしても次元削減という利点はあるかなと思ったのですが、一方で二次判別分析は、次元削減という利点がないのであれば、他の機械学習手法を使えば良いので二次判別分析を使う利点がないのではないかという気がしてきました。
assistant:
確かに、二次判別分析(QDA)は一見すると、次元削減という利点がなく、他のより高度な機械学習手法を使う方が良いのでは?と考えられます。
しかしながら、QDAには以下のような利点があります:
- 解釈可能性: QDAはパラメトリックな方法の一つで、生成モデルに基づいています。つまり、それぞれのクラスが特定の分布を持つと仮定します。そのため所属クラスの確率がどのように計算されているかを理解することが容易です。
- 計算の効率: QDAは一部の非パラメトリックな方法(例えば、K近傍法など)に比べて、訓練データに対する計算が軽量です。大量のデータがある場合でも、QDAの訓練は高速で行なえます。
- 非線形: QDAは線形ではない決定境界を作ることができるので、一部の線形では表せないクラス分布をモデル化することができます。これは例えば線形判別分析(LDA)では難しいことです。
ただし、QDAが優れた方法であるとはかぎりません。クラス間の分布が多変量ガウス分布に従うという仮定は必ずしも成り立つわけではなく、またクラスごとに異なる共分散行列を仮定すると、パラメータの数が非常に多くなり過学習のリスクも高まります。
そのため、最終的にどの手法を用いるかはデータの性質と解決すべき問題によるところが大きく、それぞれの手法の利点と欠点を理解した上で適切な判断を行うことが重要です。
user:
同じデータに対して、混合判別分析を行い、結果を可視化するコードを書いてください。
assistant:
混合線形判別分析(Mixed Linear Discriminant Analysis)や混合二次判別分析(Mixed Quadratic Discriminant Analysis)という明確な手法は存在しないように思われます。そのため、どのように混合判別分析を行いたいか、具体的な要件によります。
もし、一部の特徴に対して線形判別分析(LDA)を、他の特徴に対して二次判別分析(QDA)を使用したいと言うのであれば、これは手動で行う必要があるでしょう。具体的には、各特徴部分集合に対してLDAやQDAを個別に適用し、その結果を組み合わせるということになります。
しかし、このような混合判別分析は一般的には行われないはずです。というのも、LDAは各クラスが同一の共分散を持つという仮定に基づいているため、その仮定が妥当でない特徴空間に対してLDAを適用すると結果が不適切になる可能性があるからです。
また、QDAが各クラスで異なる共分散を許すため、一部の特徴に対して二次判別分析を行いたいというニーズがある場合は、全ての特徴に対してQDAを適用する方が自然かもしれません。
つまり、問題の要件とデータの性質によって最適な手法を選ぶべきであり、単純にLDAとQDAを「混ぜる」ことは常に有益とは限らないことを覚えておいてください。しかし具体的なシナリオや要件があれば、その内容に合わせて具体的なアドバイスやコードの提供が可能かもしれません。
user:
ありがとうございました。今日のテーマは「ChatGPTとPythonで学ぶ 線形判別分析」でしたが、「ChatGPTとPythonで学ぶ 線形判別分析と二次判別分析」に変えてもよろしいですか?
assistant:
もちろんです、そのようにテーマを変更していただいて構いません。今回のセッションでは、線形判別分析(LDA)だけでなく、二次判別分析(QDA)についても詳しく取り上げましたので、それらを反映したタイトルとすることは適切と考えられます。「ChatGPTとPythonで学ぶ 線形判別分析と二次判別分析」が新しいテーマとなります。
user:
それでは、以上の議論を踏まえて、線形判別分析と二次判別分析について詳しくまとめてください。
assistant:
しかしいです。以下に、今回の議論を踏まえて線形判別分析(LDA)と二次判別分析(QDA)についてまとめてみます。
線形判別分析(LDA)
- LDAはデータを使ってクラスを区別するための線形な決定境界を見つけます。
- LDAは生成モデルの一種であり、データが各クラスに従うガウス分布に基づいて生成されるという仮説に基づいています。
- クラスが複数存在し、特徴量が多次元であっても適用できます。
- 各クラスの共分散行列を等しく仮定します(クラス共通の共分散行列)。
- 分類だけでなく、次元削減にも利用できます。
二次判別分析(QDA)
- QDAはデータを使ってクラスを区別するための二次(非線形)な決定境界を見つけます。
- QDAも生成モデルの一種で、こちらもデータが各クラスに従うガウス分布に基づいて生成されるという仮説に基づいています。
- 各クラスが異なる共分散行列を持つと仮定します。
- 分布の形が複雑で、線形な手法ではうまく分類できない場合に有効です。
- LDAとは異なり、次元削減には利用できません。
LDAとQDAの使用時の注意
- LDAとQDAの両方とも、クラスが真にガウス分布に従って生成されるという仮説に基づいています。これらの手法を使用する際は、この仮説が妥当であるかどうかをチェックすることが大切です。
- QDAは、各クラスの共分散行列が異なると仮定します。もし、この仮定が妥当でない場合、LDAを使用した方が精度が上がる可能性があります。
- 逆に、各クラスのデータ分布が非常に異なっていて、LDAの「クラス共通の共分散行列」の仮定が妥当でない場合は、QDAを使用した方が精度が上がる可能性があります。
これにより、線形判別分析と二次判別分析についての理解が深まったことを願っています。この知識を活用して、具体的な問題解決の際に最適な手法を選択することができればと思います。
user:
最後に、以上の議論を踏まえた面白ギャグを創作してください。
assistant:
もちろんです、さっそく以下のような機械学習に関するギャグを考えてみました。
機械学習者がバーに入ってきました。
バーテンダーに向かって彼は言います、"A regular beer, please."
バーテンダーが聞き返します、"How about trying our quadratic beer? It's got complex flavors that aren't just linear!"
そこで機械学習者は返します、"Hmm, let me think. If I start with a linear beer (LDA), I can use it for both quenching my thirst and understanding its flavor complexities (dimension reduction). But if I go with a quadratic beer (QDA), I just have to deal with the increased complexity for the taste! Decisions, decisions, sigh!"
バーテンダーが笑いながら返します、"Well, that's one way of deciding on a beer!"
これが、機械学習者の困惑の日常さ。線形か二次か、専用のビールを選ぶなんて、誰もが迷いますよね!
注意: LDA(Linear Discriminant Analysis)、QDA(Quadratic Discriminant Analysis)は、通常ビールに関連付けられるわけではありません。このギャグは、機械学習に関する仮設とビール選びの困難さを楽しく表現するためのものです。
user:
日本語のラップの歌詞で表現してください。
assistant:
分析するつもりでバーへ飛び込んだ、
注文は「普通のビール」だったってことばかりなら、
バーテンが提案「どうだろう、二次のビール」
面白そうだな、馴染みがないけど。
線形ビールで十分なはずなんだ、
口当たりもいいし、次元削減も手に入るさ。
でも二次ビールはただでさえ複雑だ、
そのうえ次元削減なんてできないようだ。
そうだ、それが問題だ、まいったな。
線形あるいは二次、迷うなぁ。
しかし、それが人生だろ、考えて見つける方がいいさ。
そう、LDAとQDAだけの物語さ。